【数据结构与算法分析】第六章优先队列（堆）（二）

最新推荐文章于 2019-05-13 15:57:51 发布

原创最新推荐文章于 2019-05-13 15:57:51 发布 · 475 阅读

0 ·

CC 4.0 BY-SA版权

数据结构专栏收录该内容

19 篇文章

订阅专栏

本文深入探讨了优先队列的不同实现方式，包括d-堆、左式堆和二项队列的特点及操作方法，并提供了详细的算法实现。

【数据结构与算法分析】第六章优先队列（堆）（二）

1.d-堆

d-堆是二叉堆的简单推广，所有的节点都有d个儿子，有可能的例外是在底层，如图为一个3-堆

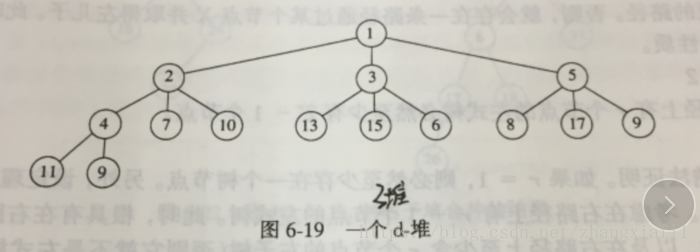
2.左式堆

左式堆具有结构特性和堆序性质。

2.1左式堆的性质

节点X的零路径长(Npl(X))：从X到一个没有两个儿子的节点的最短路径长，即具有0个或1个儿子的节点的Npl为0

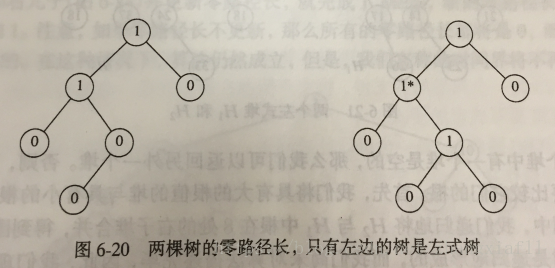
左式堆的性质：对于堆中的每一个节点X，左儿子的零路径长都大于或等于右儿子的零路径长

左式树更偏重于使树向左增加深度，有可能存在由左节点形成的长路径构成的树，因此就有了左式堆这个名称。

如图为两个左式堆：

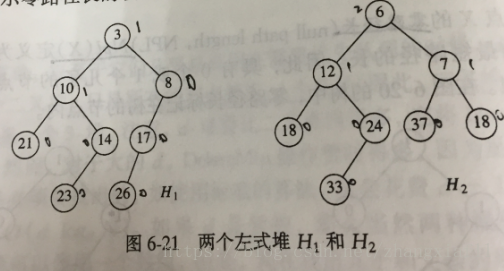
2.2左式堆的操作

基本操作为合并

（1）将具有大的根植的堆与具有小的根植的堆的右子堆合并。如图，递归的将H2与H1中根在8处的右子堆合并

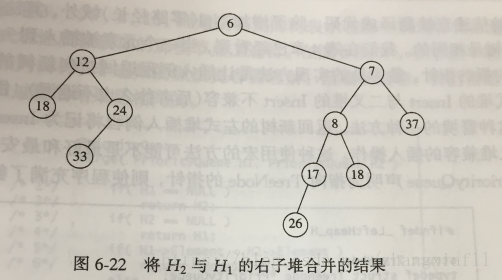
（2）让第一步形成的新的堆作为H1的根的右儿子，如图

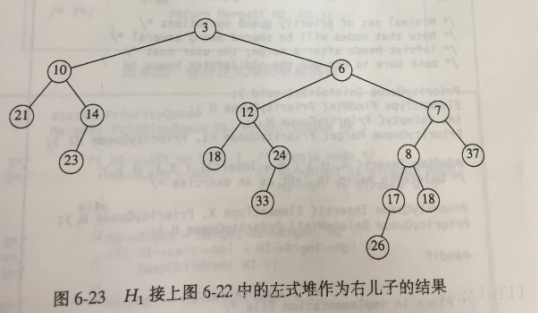
（3）交换根的左儿子和右儿子并更新零路径长，完成合并

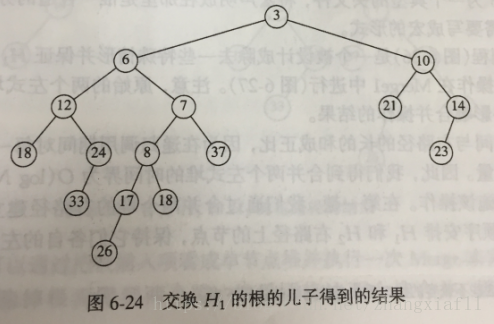
左式堆的类型声明：

#ifndef _LeftHeap_H
struct TreeNode;
typedef struct TreeNode *PriorityQueue;
PriorityQueue Initialize(void);
ElementType FindMin(PriorityQueue H);
int IsEmpty(PriorityQueue H);
PriorityQueue Merge(PriorityQueue H1,PriorityQueue H2);
#define Insert(X,H) (H=Insert1(X,H))
PriorityQueue Insert1(ElementType X,PriorityQueue H);
PriorityQueue DeleteMin1(PriorityQueue H);
#endif
struct TreeNode
{
    ElementType Element;
    PriorityQueue Left;
    PriorityQueue Right;
    int Npl;
};

合并左式堆的驱动程序：

PriorityQueue Merge(PriorityQueue H1,PriorityQueue H2)
{
    if(H1==NULL)
        return H2;
    if(H2==NULL)
        return H1;
    if(H1->Element<H2->Element)//找出两左式堆的最小根节点
        return Merge1(H1,H2);
    else
        return Merge1(H2,H1);  
}

合并左式堆的实际例程：

static PriorityQueue Merge1(PriorityQueue H1,PriorityQueue H2)
{
    if(H1->Left==NULL)
        H1->Left=H2;
    else
    {
        H1->Right=Merge(H1->Right,H2);
        if(H1->Left->Npl<H1->Right->Npl)
            SwapChildren(H1);
        H1->Npl=H1->Right->Npl+1;
    }
    return H1;
}

左式堆的插入例程：

PriorityQueue Insert1(ElementType X,PriorityQueue H)
{
    PriorityQueue SingleNode;
    SingleNode=malloc(sizeof(struct TreeNode));
    if(SingleNode==NULL)
        FatalError("out of space");
    else
    {
        SingleNode->Element=X;SingleNode->Npl=0;
        SingleNode->Left=SingleNode->Right=NULL;
        H=Merge(SingleNode,H);
    }
    return H;
}

左式堆的DeleteMin例程：

PriorityQueue DeleteMin1(PriorityQueue H)
{
    PriorityQueue LeftHeap,RightHeap;
    if(IsEmpty(H))
    {
        Error("Priority queue is empty");
        return H;
    }
    LeftHeap=H->Left;
    RightHeap=H->Right;
    free(H);
    return Merge(LeftHeap,RightHeap);
}

3.二项队列

3.1二项队列结构

二项队列不是一棵堆序的树，而是堆序树的集合，称为森林。堆序树中的每一棵树都是有约束的形式，叫做二项树。每一个高度上至多存在一棵二项树。

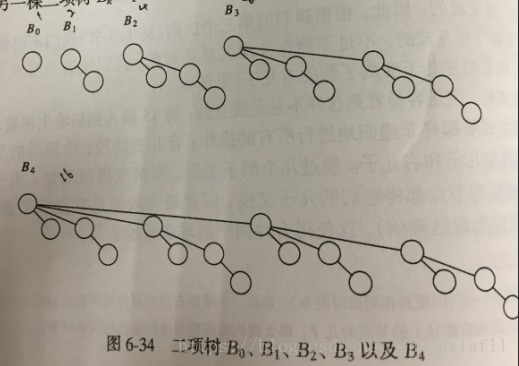
高度为0的二项树是一棵单节点树，如B0

高度为k的二项树Bk通过将一棵二项树B(k-1)附接到另一棵二项树B(k-1)的根上而构成。如B1,B2,B3,B4

二项树Bk由一个带有儿子B0,B1...B(K-1)的根组成，如B4由B0,B1,B2,B3组成，高度为k的二项树恰好有2^k个节点。

例：大小为13的优先队列可以写成1101，用森林B3,B2,B0来表示

3.2二项队列操作

合并操作：合并H1和H2

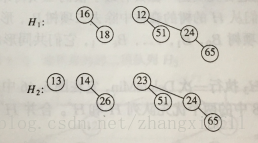
将H1和H2中高度为1的二项树合并后得到下图：

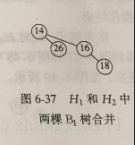
然后再将其他合并得到H3

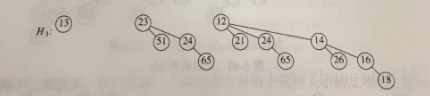
插入操作：

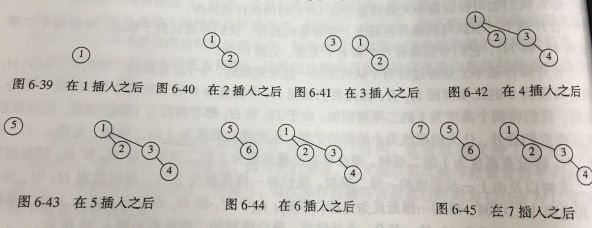
DeleteMin操作：

例：对H3执行一次DeleteMin操作，如图，H3含有森林B0,B2,B3，最小的根是12

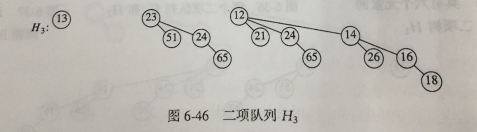
除去B3外的H3为：

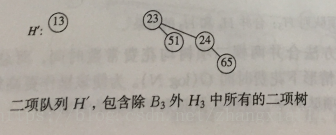
除去12后的B3为：

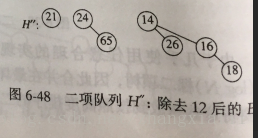
合并得：

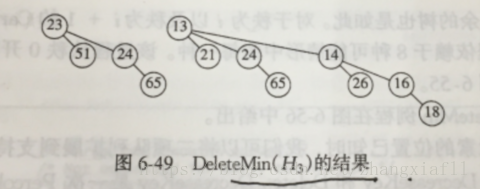
3.3二项队列的实现

DeleteMin操作需要快速找出根的所有子树的能力，因此，需要一般树的标准表示方法：

每个节点的儿子都存在一个链表中，而且每个节点都有一个指向它的第一个儿子的指针。

总之：

二项树的每一个节点将包含有：（1）数据，（2）第一个儿子（最右的儿子），（3）兄弟节点。
二项树中的儿子以递减顺序排列

例：

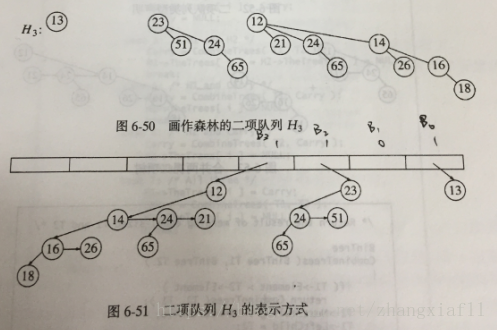
二项队列H3的表达方式，将从B3,B2,B0成降序排列，每个节点含有自身数据，第一个儿子和兄弟节点

二项队列的声明：

typedef struct BinNode *Position;
typedef struct Collection *BinQueue;
struct BinNode
{
    ElementType Element;
    Position LeftChild;
    Position NextSibling;
};
struct Collection
{
    int CurrentSize;
    BinTree TheTrees[MaxTrees];
}

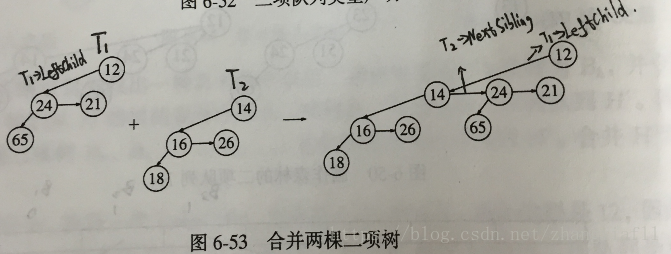
合并同样大小的两棵二项树：

BinTree CombineTrees(BinTree T1,BinTree T2)
{
    if(T1->Element>T2->Element)
        return CombineTrees(T2,T1);
    T2->NextSibling=T1->LeftChild;
    T1->LeftChild=T2;
    return T1;
}

合并两个优先队列的例程：

BinQueue Merge(BinQueue H1, BinQueue H2)
{
    BinTree T1, T2, Carry = NULL;
    int i,j;
    if(H1->CurrentSize+H2->CurrentSize>Capacity)
        Error("Exceed the Capacity");
    H1->CurrentSize = H1->CurrentSize + H2->CurrentSize;
    for(i=0,j=1;j<H1->CurrentSize;i++,j*=2)
    {
        T1 = H1->TheTrees[i];
        T2 = H2->TheTrees[i];
        switch(!!T1+2*!!T2+4*!!Carry)//如果T1存在则!!T1为1,否则为0
        {
            case 0: //No Trees
            case 1: //Only H1
                break; 
            case 2: 
                H1->TheTrees[i] = T2;
                H2->TheTrees[i] = NULL;
                break;
            case 4: //Only Carry
                H1->TheTrees[i] = Carry;
                Carry = NULL;
                break;
            case 3: //T1,T2
                Carry = CombineTree(T1,T2);
                H1->TheTrees[i] = H2->TheTrees[i] = NULL;
                break;
            case 5:
                Carry = CombineTree(T1,Carry);
                H1->TheTrees[i] = NULL;
                break;
            case 6:
                Carry = CombineTree(T2,Carry);
                H2->TheTrees[i] = NULL;
                break;
            case 7:
                H1->TheTrees[i] = Carry;
                Carry = CombineTree(T1,T2);
                H2->TheTrees[i] = NULL;
                break;
        }
    }
    return H1;
}

二项队列的DeleteMin操作：

ElementType DeleteMin(BinQueue H)
{
    int i,j;
    int MinTree;
    BinQueue DeleteQueue;
    Position DeletedTree, OldRoot;
    ElementType MinItem;
 
    if(IsEmpty(H))
    {
        Error("Empty BinQueue!!");
        return -Infinity;
    }
    //find the minmum
    Min = Infinity;
    for(i=0;i<MaxTree;i++)
    {
        if(H->TheTrees[i] && H->TheTrees[i]->Element<MinItem)
        {
            // Updata the minmun
            MiniItem = H->TheTrees[i]->Element;
            MinTree = i;
        }
    }
    // have found the DeleteTree
    DeleteTree = H->TheTrees[MinTree];
    OldRoot = DeleteTree;
    DeleteTree = OldRoot->LeftChild;
    free(OldRoot);
 
    // form the DeleteQueue
    DeletedQueue = Initialize();
    DeletedQueue->CurrentSize = (1<<MinTree) - 1;
 
    for(j=MinTree-1;j>=0;j--)
    {
        DeletedQueue->TheTree[j] = DeletedTree;
        DeletedTree = DeletedTree->Sibling;
        DeletedQueue->TheTree[j]->Sibling = NULL;
    }
    H->TheTrees[MiniTree] = NULL;
    H->CurrentSize -= DeletedQueue->CurrentSize+1;
 
    Merge(H,DeletedQueue);
    return MinItem;
 
}