LeetCode hard 84. Largest Rectangle in Histogram--python,java 15行,c++ 15行解法

最新推荐文章于 2021-06-13 19:59:01 发布

原创最新推荐文章于 2021-06-13 19:59:01 发布 · 403 阅读

0 ·

CC 4.0 BY-SA版权

LeetCode 同时被 3 个专栏收录

122 篇文章

订阅专栏

python-做题

100 篇文章

订阅专栏

java-做题

55 篇文章

订阅专栏

本文介绍了一种使用栈解决最大矩形面积问题的高效算法。该算法可在O(N)的时间复杂度内找到直方图中最大矩形的面积，并提供了Java、C++及Python三种语言的实现示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目地址：

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

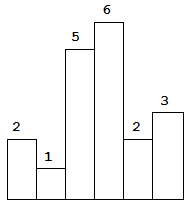
在这里插入图片描述

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

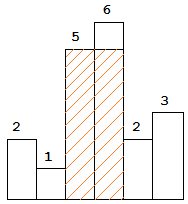
在这里插入图片描述

The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

Input: [2,1,5,6,2,3]
Output: 10

这道题目推荐看官方解答，非常详细：Largest Rectangle In Histogram - LeetCode Articles
其中最巧妙的解法是使用栈，空间的复杂度是O(N)，时间的复杂度据官方说法也是O(N)，我不是很清楚，有知道的人可以告诉我一声。

java解法：

public class Solution {
    public int largestRectangleArea(int[] heights) {
        Stack < Integer > stack = new Stack < > ();
        stack.push(-1);
        int maxarea = 0;
        for (int i = 0; i < heights.length; ++i) {
            while (stack.peek() != -1 && heights[stack.peek()] >= heights[i])
                maxarea = Math.max(maxarea, heights[stack.pop()] * (i - stack.peek() - 1));
            stack.push(i);
        }
        while (stack.peek() != -1)
            maxarea = Math.max(maxarea, heights[stack.pop()] * (heights.length - stack.peek() -1));
        return maxarea;
    }
}

c++解法：

class Solution {
public:
    int largestRectangleArea(vector<int>& A) {
        int n = A.size(), ans = 0, pos = 0;
        stack<int> st;
        for (int i = 0; i <= n; i++) {
            while (!st.empty() && (i == n || A[st.top()] >= A[i])) {
                pos = st.top(); st.pop();
                ans = max(ans, A[pos] * (st.empty() ? i : i-st.top()-1));
            }
            st.push(i);
        }
        return ans;
    }
};

Python解法：

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        heights.append(0)
        stack = [-1]
        ans = 0
        for i in range(len(heights)):
            while heights[i] < heights[stack[-1]]:
                h = heights[stack.pop()]
                w = i - stack[-1] - 1
                ans = max(ans, h * w)
            stack.append(i)
        heights.pop()
        return ans