基于FPGA的CORDIC算法的实现（1）

最新推荐文章于 2022-09-06 23:31:33 发布

原创

最新推荐文章于 2022-09-06 23:31:33 发布 · 5.6k 阅读

51 ·

CC 4.0 BY-SA版权

本文深入探讨了CORDIC算法的向量模式原理，详细解析了其在FPGA上的实现过程，包括MATLAB仿真验证及代码优化技巧，适合于信号处理、嵌入式系统设计领域的工程师和研究人员。

CORDIC算法向量模式原理介绍及FPGA实现

参考文献
项目简述
CORDIC算法向量模式原理
MATLAB实现
FPGA实现
MATLAB测试代码
总结

参考文献

[1].liyuanbhu
[2].碎碎思
[3].电子发烧友(这门课里面的代码写的非常棒，建议有条件的同学可以与板卡一起购买，记住一定是带着板卡，这里不再多说)

项目简述

基本上懂点FPGA信号处理操作的同学都听过CORDIC算法，该算法可以被使用计算常见函数及超越函数。那么喜欢刨根问底的同学就会问为什么CORDIC算法可以被使用来计算常见函数，该算法又可以使用计算哪些函数，精度如何等等问题。那么这篇文章及接下来的文章将用来介绍这些问题，其实关于该算法在优快云上面已经又比较完善的优快云博主进行了介绍，包括我也是使用上面的博客进行的学习，博主的连接以及一些参考文献会在文章的最后给出。

首先CORDIC的全称是 Coordinate Rotation Digital Computer 也就是我们常说的坐标旋转算法。既然是坐标旋转算法，那么就需要坐标进而坐标系是必须需要提前确定。常见在CORDIC算法中使用的系统有圆周系统、线性系统、双曲系统，每种系统又分为向量模式与旋转模式，每种模式可以使用计算不同的函数。包括如果掌握了CORDIC的原理计算一些其他特殊函数也是可能的。 CORDIC函数可以使用计算的函数如下：
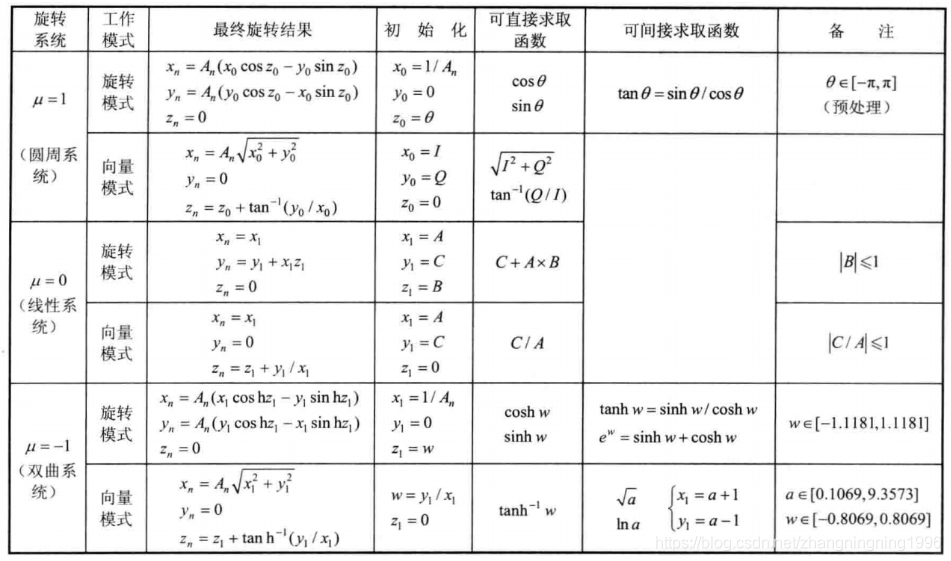
在这里插入图片描述
下面是VIVADO中CORDIC IP中可以计算的函数

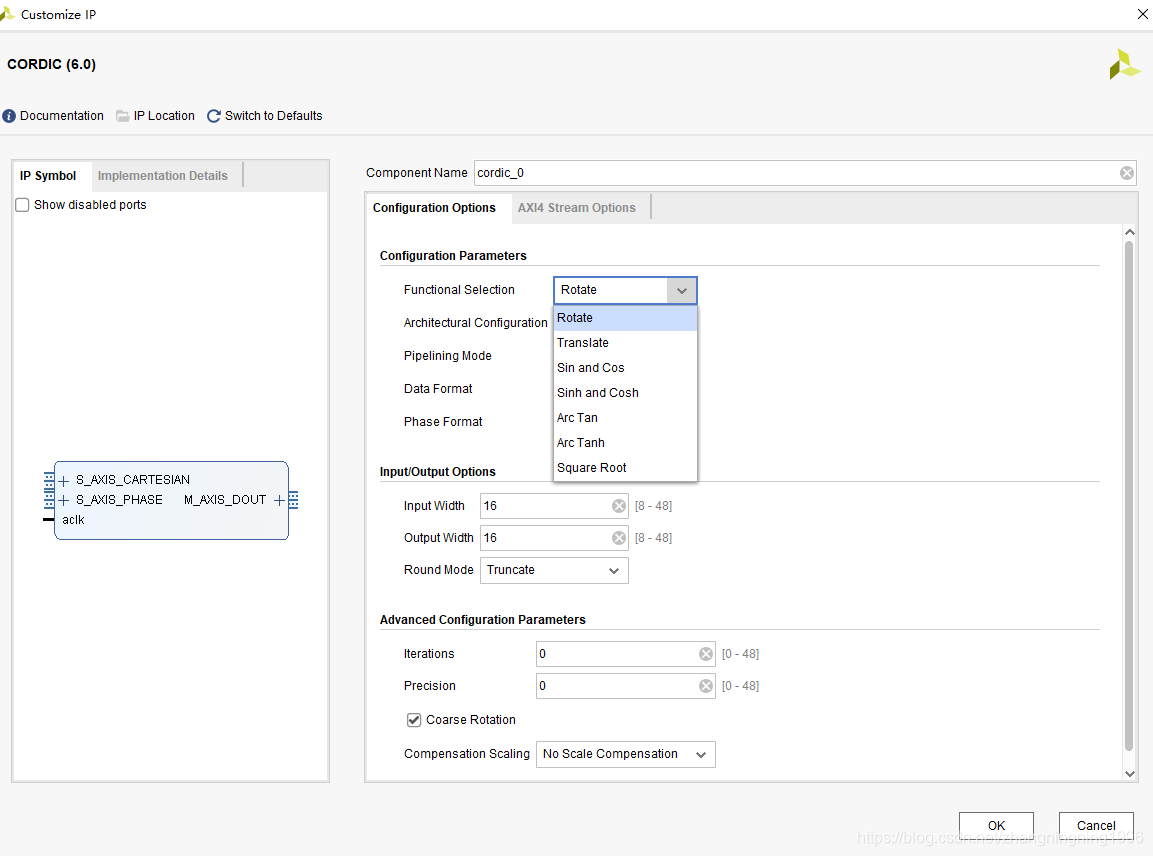
这里是不是可以看出上面的函数基本上是一一对应的。

CORDIC算法向量模式原理

CIRDIC算法向量模式推导步骤一

这里主要参考的是参考文献[1]中的文章，大家可以进行相应的阅读。
平面上一点在直角坐标系下的坐标（X,Y）=（100，200），如何求的在极坐标系下的坐标（ρ,θ）。用计算器计算一下可知答案是（223.61，63.435）。
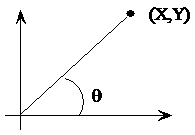
在这里插入图片描述
为了突出重点，这里我们只讨论X和Y都为正数的情况。这里或许有同学要说如果X和Y中有为负值的情况应该咋么办，其实这部分的算法不需要X和Y都为正值，但是需要X为正值。如果X为负值，那么我们便需要进行相应的处理，方法就是将X轴的值变成正值，但是这部分不要忘记CORDIC迭代的初始值发生变化。当X变成正值之后θ=atan(y/x)。求θ的过程也就是求atan 函数的过程。Cordic算法采用的想法很直接，将 $(x, y)$ 旋转一定的度数，如果旋转完纵坐标变为了0，那么旋转的度数就是θ。坐标旋转的公式可能大家都忘了，这里把公式列出了。设 $(x, y)$ 是原始坐标点，将其以原点为中心，顺时针旋转θ之后的坐标记为 $x_1,y_1)$ ,则有如下公式：
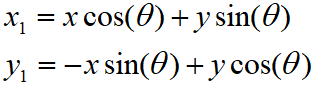
在这里插入图片描述
这里要明确我们的目标是为了将 $y$ 变成零，为了减少计算量，都是先用二分法进行旋转，也就是说第一次旋转45度，至于是顺时针旋转还是逆时针旋转取决于 $y$ 的符号。

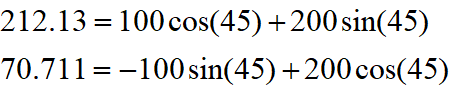
旋转之后纵坐标为70.71，还是大于0，说明旋转的度数不够，接着再旋转22.5度。
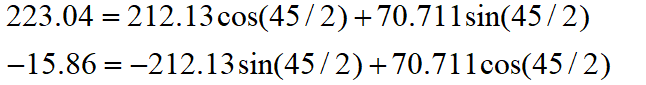
在这里插入图片描述
这时总共旋转了45+22.5=67.5度。结果纵坐标变为了负数，说明θ<67.5度，这时就要往回转，还是二分查找法的思想，这次转11.25度。

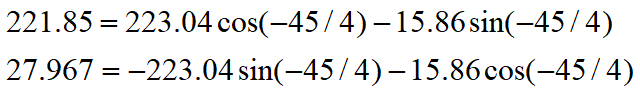
这时总共旋转了45+22.5-11.25=56.25度。又转过头了，接着旋转，这次顺时针转5.625度。
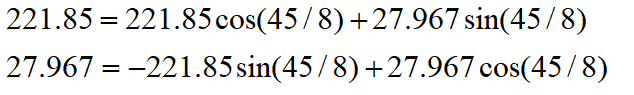
在这里插入图片描述
这时总共旋转了45+22.5-11.25+5.625=61.875度。这时纵坐标已经很接近0了。我们只是说明算法的思想，因此就不接着往下计算了。计算到这里我们给的答案是 61.875±5.625。二分查找法本质上查找的是一个区间，因此我们给出的是θ值的一个范围。同时，坐标到原点的距离ρ也求出来了，ρ=223.52。与标准答案比较一下计算的结果还是可以的。旋转的过程图示如下。
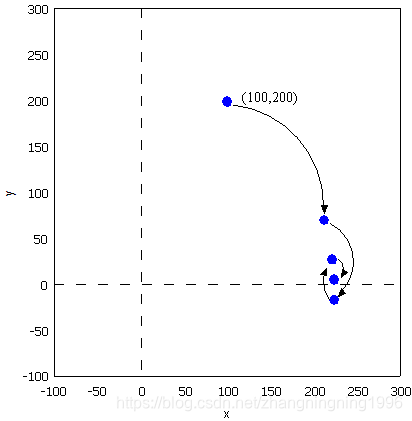
在这里插入图片描述
可能有读者会问，计算中用到了 sin 函数和 cos 函数，这些值又是怎么计算呢。很简单，我们只用到很少的几个特殊点的sin 函数和 cos 函数的值，提前计算好存起来，用查找表。这里需要注意，这种思想在FPGA中非常容易遇见。

将上面的思想我们使用MATLAB来实现如下：

clc;
clear all;

sine = [0.7071067811865,0.3826834323651,0.1950903220161,0.09801714032956,0.04906767432742,0.02454122852291,0.01227153828572,0.006135884649154,0.003067956762966,0.001533980186285,7.669903187427045e-4,3.834951875713956e-4,1.917475973107033e-4,9.587379909597735e-5,4.793689960306688e-5,2.396844980841822e-5];
cosine = [0.7071067811865,0.9238795325113,0.9807852804032,0.9951847266722, ...
0.9987954562052,0.9996988186962,0.9999247018391,0.9999811752826,0.9999952938096, ...
0.9999988234517,0.9999997058629,0.9999999264657,0.9999999816164,0.9999999954041, ...
0.999999998851,0.9999999997128];
angle = 45;
a = zeros(16,1);
for i = 1:16
    a(i) = angle;
    angle = angle/2;
end

 x = 100;
 y = -300;
 z = 0;
 
for i = 1:16
    if(y > 0)
        x_new = x*cosine(i) + y*sine(i);
        y_new = y*cosine(i) - x*sine(i);
        x = x_new;
        y = y_new;
        z = z + a(i);
    else
        x_new = x*cosine(i) - y*sine(i);
        y_new = y*cosine(i) + x*sine(i);
        x = x_new;
        y = y_new;
        z = z - a(i);
    end
end
z

结果如下：
在这里插入图片描述

CIRDIC算法向量模式推导步骤二

CORDIC一般是在FPGA中实现。FPGA中的DSP资源是非常宝贵的资源，所以我们要尽可能减少CORDIC中的乘法的个数，所以将公式变形如下：
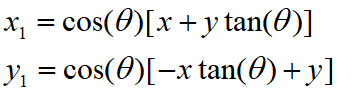
在这里插入图片描述
这里因为我们要计算相位 $a r c t a n (y / x)$ ，所以我们先将缩放因子去掉

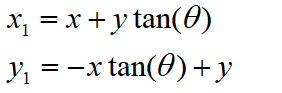
但是我们注意到 CIRDIC算法向量模式不仅可以计算 $a r c t a n (y / x)$ 而且可以计算 $\sqrt{x^2+y^2}$ ，所以这个补偿因子到最后肯定会补偿回来，在FPGA中同样利用查表得方法补偿回来。
省略cos(θ)后发生了什么呢，每次旋转后的新坐标点到原点的距离都变长了，放缩的系数是1/cos(θ)。不过没有关系，我们求的是θ，不关心ρ的改变。这样的变形非常的简单，但是每次循环的运算量一下就从4次乘法降到了2次乘法了。

将上面的思想我们使用MATLAB来实现如下：

clc;
clear all;

tangent = [1.0,0.4142135623731,0.1989123673797,0.09849140335716,0.04912684976947, ...
0.02454862210893,0.01227246237957,0.006136000157623,0.003067971201423, ... 
0.001533981991089,7.669905443430926e-4,3.83495215771441e-4,1.917476008357089e-4, ... 
9.587379953660303e-5,4.79368996581451e-5,2.3968449815303e-5];
angle = 45;
a = zeros(16,1);
for i = 1:16
    a(i) = angle;
    angle = angle/2;
end

 x = 100;
 y = -300;
 z = 0;
 
for i = 1:16
    if(y > 0)
        x_new = x+ y*tangent(i);
        y_new = y - x*tangent(i);
        x = x_new;
        y = y_new;
        z = z + a(i);
    else
        x_new = x- y*tangent(i);
        y_new = y + x*tangent(i);
        x = x_new;
        y = y_new;
        z = z - a(i);
    end
end
z

在这里插入图片描述
结果与公式变形前得结果一摸一样，进而说明了我们实验得正确性。

CIRDIC算法向量模式推导步骤三

在FPGA中多得是寄存器查找表等资源，DSP资源非常少，所以我们要尽可能得消除CORDIC中得乘法，消除得方法是变下面公式中得乘法为移位操作：
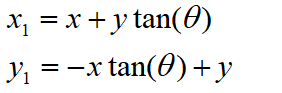
在这里插入图片描述
所以我们要求 $t a n (θ)$ 是2得负整数次幂。然后我们对上面得式子进行分析：
第一次循环时，tan(45)=1，所以第一次循环实际上是不需要乘法运算的。第二次运算呢？

Tan(22.5)=0.4142135623731,很不幸，第二次循环乘数是个很不整的小数。是否能对其改造一下呢？答案是肯定的。第二次选择22.5度是因为二分查找法的查找效率最高。如果选用个在22.5到45度之间的值，查找的效率会降低一些。如果稍微降低一点查找的效率能让我们有效的减少乘法的次数，使最终的计算速度提高了，那么这种改进就是值得的。

我们发现tan(26.565051177078)=0.5，如果我们第二次旋转采用26.565051177078度，那么乘数变为0.5，如果我们采用定点数运算的话（没有浮点协处理器时为了加速计算我们会大量的采用定点数算法）乘以0.5就相当于将乘数右移一位。右移运算是很快的，这样第二次循环中的乘法运算也被消除了。

类似的方法，第三次循环中不用11.25度，而采用 14.0362434679265 度。

Tan(14.0362434679265)= 1/4

乘数右移两位就可以了。剩下的都以此类推。

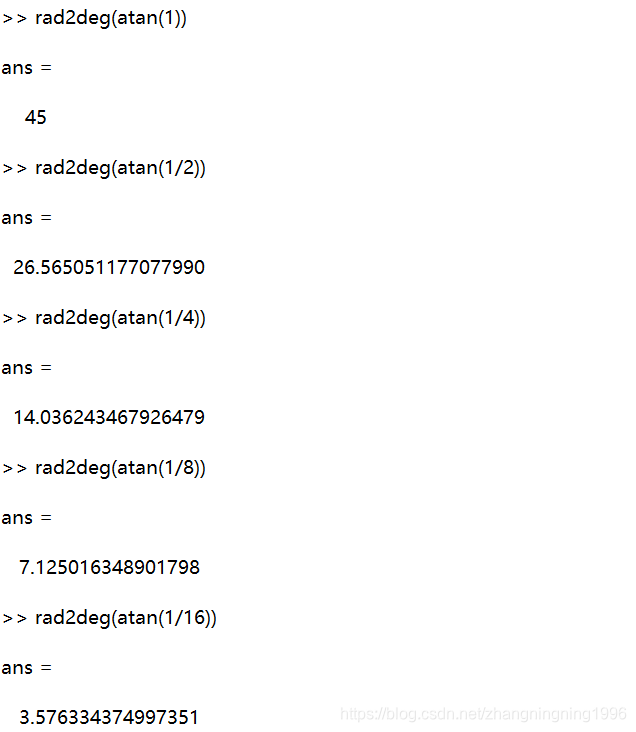
在这里插入图片描述
所以我们给出相应的MATLAB代码：

clc;
clear all;

angle = [45.0, 26.565051177078, 14.0362434679265, 7.1250163489018, 3.57633437499735, ...
                            1.78991060824607, 0.8951737102111, 0.4476141708606, 0.2238105003685, 0.1119056770662, ... 
                            0.0559528918938, 0.027976452617, 0.01398822714227, 0.006994113675353, 0.003497056850704,0.001748528426980];
                     
tangent = [1.0, 1 / 2.0, 1 / 4.0, 1 / 8.0, 1 / 16.0, ...
                              1 / 32.0, 1 / 64.0, 1 / 128.0, 1 / 256.0, 1 / 512.0, ...
                              1 / 1024.0, 1 / 2048.0, 1 / 4096.0, 1 / 8192.0, 1 / 16384.0,1/32768];


 x = 100;
 y = -300;
 z = 0;
 
for i = 1:16
    if(y > 0)
        x_new = x+ y*tangent(i);
        y_new = y - x*tangent(i);
        x = x_new;
        y = y_new;
        z = z + angle(i);
    else
        x_new = x- y*tangent(i);
        y_new = y + x*tangent(i);
        x = x_new;
        y = y_new;
        z = z - angle(i);
    end
end
z

上面的程序由于MATLAB本身不利于移位操作，所以我们也就乘以了相应的数，但这点在FPGA中是相当容易操作的。
运行结果如下：
在这里插入图片描述
到这里 CORDIC 算法的最核心的思想就介绍完了。当然，这里介绍的只是CORDIC算法最基本的内容，实际上，利用CORDIC 算法不光可以计算 atan 函数，其他的像 Sin，Cos，Sinh，Cosh 等一系列的函数都可以计算。

CIRDIC算法向量模式推导步骤三

上面为计算过程中我们将 $c o s (θ)$ 省略，所以为了计算 $\sqrt{x^2+y^2}$ ，所以这个补偿因子到最后肯定会补偿回来。因为每次推导我们都省略了 $c o s (θ)$ ，所以我们最终的真实值 $x_{n1},y_{n1})$ 需要进行的缩放处理如下：
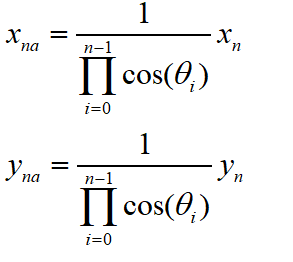
在这里插入图片描述
由前面可知：

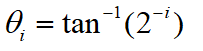
所以：

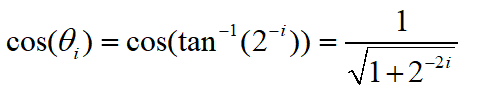
若总的旋转次数为n，则总的模长补偿因子K可表示为:

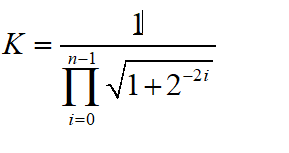
当n趋于无穷大时，K 逼近 0.607252935。
对应的MATLAB程序如下：

clc;
clear all;

angle = [45.0, 26.565051177078, 14.0362434679265, 7.1250163489018, 3.57633437499735, ...
                            1.78991060824607, 0.8951737102111, 0.4476141708606, 0.2238105003685, 0.1119056770662, ... 
                            0.0559528918938, 0.027976452617, 0.01398822714227, 0.006994113675353, 0.003497056850704,0.001748528426980];
                     
tangent = [1.0, 1 / 2.0, 1 / 4.0, 1 / 8.0, 1 / 16.0, ...
                              1 / 32.0, 1 / 64.0, 1 / 128.0, 1 / 256.0, 1 / 512.0, ...
                              1 / 1024.0, 1 / 2048.0, 1 / 4096.0, 1 / 8192.0, 1 / 16384.0,1/32768];


 x = 100;
 y = -300;
 z = 0;
 
for i = 1:16
    if(y > 0)
        x_new = x+ y*tangent(i);
        y_new = y - x*tangent(i);
        x = x_new;
        y = y_new;
        z = z + angle(i);
    else
        x_new = x- y*tangent(i);
        y_new = y + x*tangent(i);
        x = x_new;
        y = y_new;
        z = z - angle(i);
    end
end
K = 1;
for i = 1:16
    K = K*1/sqrt(1+2^-(2*(i-1)));
end
x_new = x_new*K

z

运行结果如下：
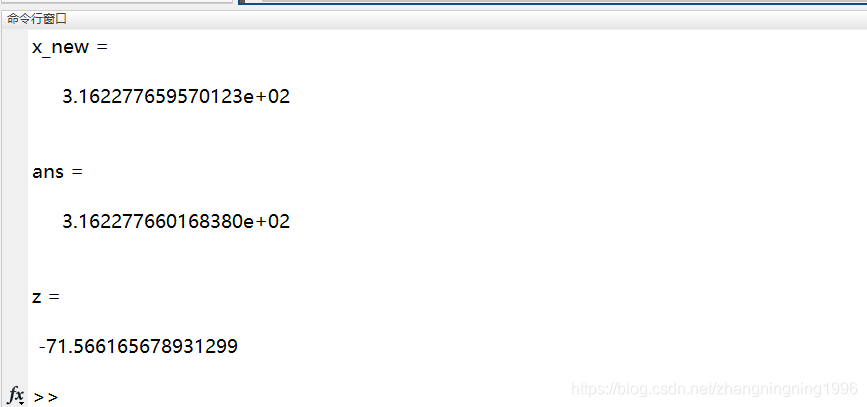
在这里插入图片描述
从上面可以验证我们实验的正确性，并且K值在实际FPGA中也是进行查表而不是上面程序那样计算。

MATLAB实现

上面的MATLAB代码知识为了验证我们的推导过程专门写的代码，这样写的代码没办法与FPGA内部生成的代码一一对应起来，其中最主要的原因也是因为没有对数据进行相应的量化操作，也没有在程序中进行相应的预处理操作。所以接下来给出相应的完整的代码，这部分代码参考了电子发烧友，本来想自己写，但是架不住别人写的代码太好，相应的链接已经在参考文献中给出，需要的同学可以自己学习。

clc;
clear all;
Ninter = 12;%迭代次数
N = 32;
%y: y坐标值(Q（N,N-2))
%x: x坐标值(Q（N,N-2))
%angle:Q(18,15)
%这些量化指标都是为了与FPGA中的一致才进行这样精度的量化
ang = quantizer('mode','fixed','roundmode','nearest','overflowmod','saturate','format',[18,15]);
input = quantizer('mode','fixed','roundmode','floor','overflowmod','saturate','format',[N,N-2]);
amp = quantizer('mode','fixed','roundmode','floor','overflowmod','saturate','format',[N,N-2]);
ampcoe = quantizer('mode','fixed','roundmode','nearest','overflowmod','saturate','format',[18,16]);
amp2 = quantizer('mode','fixed'</