package zuoye13;
import Switch1.S;
import java.util.Arrays;
public class SortTest {
public static void main(String[] args) {
int arr[]={1,2,3,4,56,7,5,4,6,9};
int arr1[]={1,2,3,4,56,7,5,4,6,9};
int arr2[]={1,2,3,4,56,7,5,4,6,9};
int arr3[]={1,2,3,4,56,7,5,4,6,9};
int arr4[]={1,2,3,4,56,7,5,4,6,9};
int arr5[]={1,2,3,4,56,7,5,4,6,9};
int arr6[]={1,2,3,4,56,7,5,4,6,9};
System.out.println("/**********************冒泡排序*********************************************************/");
long sysDate1= System.currentTimeMillis();
for(int i=0;i<100000;i++) {
dubbleSort(arr);
}
long sysDate2=System.currentTimeMillis();
System.out.println(Arrays.toString(arr));
System.out.println(sysDate2-sysDate1);
System.out.println("/********************选择排序***********************************************************/");
//
long selectdate1= System.currentTimeMillis();
for(int i1=0;i1<100000;i1++) {
SelectSort(arr1);
}
long selectdate2=System.currentTimeMillis();
System.out.println(Arrays.toString(arr1));
System.out.println(selectdate2-selectdate1);
System.out.println("/*********************直接插入排序**********************************************************/");
//直接插入排序
long Insertdate1= System.currentTimeMillis();
for(int i1=0;i1<100000;i1++) {
InsertSort(arr2);
}
long Insertdate2=System.currentTimeMillis();
System.out.println(Arrays.toString(arr2));
System.out.println(Insertdate2-Insertdate1);
System.out.println("/********************快速排序***********************************************************/");
//快速排序
long quickdate1= System.currentTimeMillis();
for(int i=0;i<100000;i++) {
InsertSort(arr3);
}
long quickdate2=System.currentTimeMillis();
System.out.println(Arrays.toString(arr3));
System.out.println(quickdate2-quickdate1);
System.out.println("/********************归并排序***********************************************************/");
// 归并排序
long mergedate1= System.currentTimeMillis();
for(int i=0;i<100000;i++) {
mergingSort(arr4);
}
long mergedate2=System.currentTimeMillis();
System.out.println(Arrays.toString(arr4));
System.out.println(mergedate2-mergedate1);
System.out.println("/******************希尔排序*************************************************************/");
//希尔排序
long shelldate1= System.currentTimeMillis();
for(int i=0;i<100000;i++) {
shellSort(arr5);
}
long shelldate2= System.currentTimeMillis();
System.out.println(Arrays.toString(arr5));
System.out.println(shelldate2-shelldate1);
System.out.println("/*********************堆排序**********************************************************/");
// 堆排序
long heapdate1= System.currentTimeMillis();
for(int i=0;i<100000;i++) {
heapSort(arr6);
}
System.out.println(Arrays.toString(arr6));
long heapdate2= System.currentTimeMillis();
System.out.println(heapdate2-heapdate1);
}
/*******************************************************************************/
//冒泡排序
/*
* <li>比较相邻的元素。如果第一个比第二个大,就交换他们两个。</li>
* <li>对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。</li>
* <li>针对所有的元素重复以上的步骤,除了最后一个。</li>
* <li>持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。</li>
*/
public static void dubbleSort(int []arr){
if(arr==null||arr.length==1){
return;
}
int temp;
boolean flag=false; //定义flag,来优化{1,2,3,4,5,7}
for(int i=0;i<arr.length-1;i++){
for(int j=i+1;j<arr.length;j++){
if(arr[i]>arr[j]){
//交换位置
temp= arr[i];
arr[i]= arr[j];
arr[j]=temp;
//每次交换后改变flag的值
flag=true;
}
}
}
if(flag==false){ //如果没发生交换,就直接打印
return;
}
}
/*******************************************************************************/
//选择排序
/*
* <li>在未排序序列中找到最小元素,存放到排序序列的起始位置</li>
* <li>再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾。</li>
* <li>以此类推,直到所有元素均排序完毕。</li>
*/
public static void SelectSort(int []arr){
if(arr==null||arr.length==1){
return;
}
int temp; //交换用的值
for(int i=0;i<arr.length;i++){
int min=i; //用来存每次的最小的角标
//用for找最小值
for(int j=i;j<arr.length;j++){
if(arr[min]>arr[j]){
min=j;
}
}
//min为最小值的角标
temp=arr[min]; //temp每次接受最小值
arr[min]=arr[i];
arr[i]=temp;
}
}
/**********************************************************************************/
//直接插入排序
/*
* <li>从第一个元素开始,该元素可以认为已经被排序</li>
* <li>取出下一个元素,在已经排序的元素序列中从后向前扫描</li>
* <li>如果该元素(已排序)大于新元素,将该元素移到下一位置</li>
* <li>重复步骤3,直到找到已排序的元素小于或者等于新元素的位置</li>
* <li>将新元素插入到该位置中</li>
* <li>重复步骤2</li>
*/
public static void InsertSort(int []arr){
int temp,i,j;
if(arr==null||arr.length==1){
return;
}
for( i=1; i<arr.length; i++) {
temp = arr[i];
for(j = i; j > 0 && temp <arr[j-1]; j--)
arr[j] = arr[j-1];
arr[j] = temp;
}
}
/**********************************************************************************/
//快速排序
/*
* <li>从数列中挑出一个元素,称为“基准”</li>
* <li>重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分割之后,
* 该基准是它的最后位置。这个称为分割(partition)操作。</li>
* <li>递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。</li>
*/
public static void quickSort(int[] numbers, int start, int end) {
//
if (start < end) {
int base = numbers[start]; // 选定的基准值(第一个数值作为基准值)
int temp; // 记录临时中间值
int i = start, j = end;
do {
while ((numbers[i] < base) && (i < end))
i++;
while ((numbers[j] > base) && (j > start))
j--;
if (i <= j) {
temp = numbers[i];
numbers[i] = numbers[j];
numbers[j] = temp;
i++;
j--;
}
} while (i <= j);
if (start < j)
quickSort(numbers, start, j);
if (end > i)
quickSort(numbers, i, end);
}
}
/**********************************************************************************/
//归并排序
/*
* <li>申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列</li>
* <li>设定两个指针,最初位置分别为两个已经排序序列的起始位置</li>
* <li>比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置</li>
* <li>重复步骤3直到某一指针达到序列尾</li>
* <li>将另一序列剩下的所有元素直接复制到合并序列尾</li>
*/
public static void mergingSort(int []a){
sort(a,0,a.length-1);
}
public static void sort(int[] data, int left, int right) {
if(left<right){
//找出中间索引
int center=(left+right)/2;
//对左边数组进行递归
sort(data,left,center);
//对右边数组进行递归
sort(data,center+1,right);
//合并
merge(data,left,center,right);
}
}
public static void merge(int[] data, int left, int center, int right) {
int [] tmpArr=new int[data.length];
int mid=center+1;
//third记录中间数组的索引
int third=left;
int tmp=left;
while(left<=center&&mid<=right){
//从两个数组中取出最小的放入中间数组
if(data[left]<=data[mid]){
tmpArr[third++]=data[left++];
}else{
tmpArr[third++]=data[mid++];
}
}
//剩余部分依次放入中间数组
while(mid<=right){
tmpArr[third++]=data[mid++];
}
while(left<=center){
tmpArr[third++]=data[left++];
}
//将中间数组中的内容复制回原数组
while(tmp<=right){
data[tmp]=tmpArr[tmp++];
}
}
/**********************************************************************************/
//希尔排序
public static void shellSort(int []a){
double d1=a.length;
int temp=0;
while(true){
d1= Math.ceil(d1/2);
int d=(int) d1;
for(int x=0;x<d;x++){
for(int i=x+d;i<a.length;i+=d){
int j=i-d;
temp=a[i];
for(;j>=0&&temp<a[j];j-=d){
a[j+d]=a[j];
}
a[j+d]=temp;
}
}
if(d==1)
break;
}
}
/**********************************************************************************/
//堆排序
/*
1、建堆(逻辑上的)
2、 调整大根堆,堆顶元素和堆中相对最后的元素进行交换
(相对于最后一个元素是待排序数据中最大值)
3、缩小堆
*/
public static void adjust(int []arr,int begin,int end){
//begin为倒数第一个非叶子节点开始
//从第一个非叶子节点往上调
int temp=arr[begin];
for(int i=begin*2+1;i<=end;i=2*i+1){
if(i+1<=end && arr[i]<arr[i+1]){ //&&位运算前后表达式交换后造成数组下标越界
i=i+1; //保存左右中的最大值
}
if(temp<arr[i]) { //大于begin的值,才交换 //temp不能是arr[begin]
arr[begin] = arr[i];
begin = i;
}
else{
break;
}
}
//跳出后,最后一个节点为空的(假设比temp大,往上移动了)
arr[begin]=temp;
}
public static void heapSort(int []arr){
//建立大根堆(多次调整adjust)
// 从倒数第一个非叶子节点开始,到0号下标
for(int i=(arr.length-1-1)/2;i>=0;i--){
adjust(arr,i,arr.length-1);
}
//在第一次后,有堆排序的结构。那么接下来就可以从0号下标开始调整
for(int i=0;i<arr.length;i++) {
int temp =arr[arr.length-1-i];
arr[arr.length-1-i]=arr[0];
arr[0]=temp;
adjust(arr,0,arr.length-1-i-1); //
}
}
}
输出结果:
排序结果和运行100000次的时间
/**********************冒泡排序*********************************************************/
[1, 2, 3, 4, 4, 5, 6, 7, 9, 56]
7
/********************选择排序***********************************************************/
[1, 2, 3, 4, 4, 5, 6, 7, 9, 56]
12
/*********************直接插入排序**********************************************************/
[1, 2, 3, 4, 4, 5, 6, 7, 9, 56]
4
/********************快速排序***********************************************************/
[1, 2, 3, 4, 4, 5, 6, 7, 9, 56]
2
/********************归并排序***********************************************************/
[1, 2, 3, 4, 4, 5, 6, 7, 9, 56]
59
/******************希尔排序*************************************************************/
[1, 2, 3, 4, 4, 5, 6, 7, 9, 56]
13
/*********************堆排序**********************************************************/
[1, 2, 3, 4, 4, 5, 6, 7, 9, 56]
11
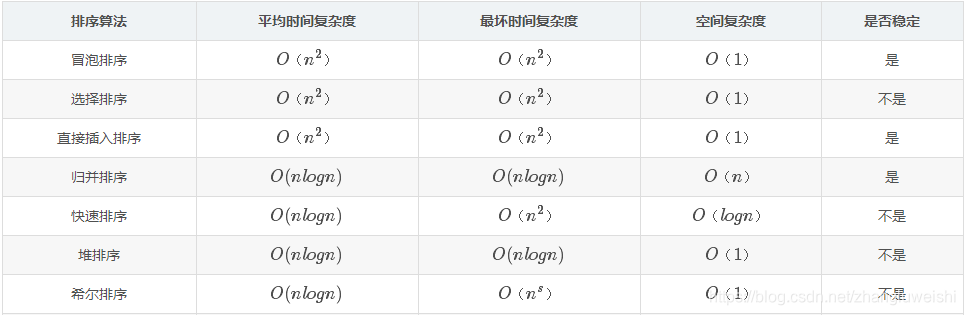
排序算法的空间、时间复杂度、稳定性





















 462
462

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








