Bounding-box regression

最新推荐文章于 2023-12-05 20:54:59 发布

leo_fighting

最新推荐文章于 2023-12-05 20:54:59 发布

阅读量201

点赞数

分类专栏：深度学习 Object Detection

本文链接：https://blog.youkuaiyun.com/zhangliaobet/article/details/99685785

版权

深度学习同时被 2 个专栏收录

9 篇文章

订阅专栏

Object Detection

7 篇文章

订阅专栏

1. 输入：N 个训练对

$\left \{ \left ( P^i,G^i \right ) \right \}_{i=1,...,N}$ ，其中， $P^i = \left ( P^i_x, P^i_y, P^i_w, P^i_h \right )$ 表示的是Proposal的中心点坐标和宽高。

方便叙述，以下公式中上标i均略去显示。

另外， $G = \left ( G_x, G_y, G_w, G_h \right )$ 表示的是Ground-truth 的中心点坐标和宽高。

2.输出：预测的 ground-truth 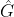$\hat{G}$

边框回归的目标是学习一种映射关系，来完成Proposal Ｐ到 ground-truth G的映射。

首先通过 $d_x\left ( P \right )$ 和 $d_y\left ( P \right )$ 完成中心点的平移，再通过 $d_w\left ( P \right )$ 和 $d_h\left ( P \right )$ 完成尺度的缩放

$\begin{align} \hat{G_x} = P_wd_x(P) + P_x \qquad \\ \hat{G_y} = P_hd_y(P) + P_y \qquad \\ \hat{G_w} = P_wexp(d_w(P)) \qquad \\ \hat{G_h} = P_hexp(d_h(P)) \qquad \end{align}$

每个函数 $d_{\star}(P)(where \;\star\; is \;one\; \;of\; x,y,h,w )$ 可以被表示为Proposal P的 pool5 特征的线性函数，记为 $\phi_{5}(P)$ 。

即有： $d_{\star}(P) = \mathbf{w^T_\star\phi_{5}(P)}$ ，其中 $w_\star$ 是可学习的模型参数向量。

$w_\star$ 可通过优化正则化的最小均方误差损失学习到：

$\mathbf{w_\star} = \underset{\mathbf{\hat{w}_\star}}{argmin\sum_{i}^{N}} \left ( t^i_{\star} - \mathbf{\hat{w}^T_\star\phi_{5}(P)}\right )^2 + \lambda \left \| \mathbf{\hat{w}_\star} \right \|^2$