概率分析和随机算法_雇佣问题

最新推荐文章于 2024-07-01 01:38:33 发布
原创 最新推荐文章于 2024-07-01 01:38:33 发布 · 1k 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

在《概率分析和随机算法_雇佣问题》中，讨论了一个办公室助理雇佣问题。问题涉及到当面试者按随机顺序出现时，预期雇佣成本的计算。最坏情况下的成本是每个面试者都需要支付费用，而最佳情况下只需支付一次费用。通过概率分析，假定应聘者顺序为均匀随机排列，预计的雇佣成本是Ci*n + Ch*lg(n)。文章还提到了两种实现一致性随机排列的方法：排序法和换位法。

The Hiring Problem

问题描述
假设你要雇佣一个新的办公室助理，雇佣代理每天想你推荐一个应聘者（连续推荐n个），你面试这个人，如果这个应聘者比目前的办公室助理更优秀，你就会辞掉当前的办公室助理，然后聘用这个新的。面试一个人需付给雇佣代理一笔费用，聘用办公助理也需要费用。

伪代码描述
最坏情形下，我们雇佣了每一个面试者
在这里插入图片描述
代价模型
在这里插入图片描述
Best Case 第一个最优 Cost = Ci·n+Ch
Worst Case 每次面试结果都是招聘新的 Ci·n+Ch·n
问题的期望是什么即 我们雇佣人数m的期望

概率分析
我们既不能得知应聘者出现的顺序，也不能控制这个顺序，因此我们使用概率分析。概率分析就是在问题的分析中使用概率技术。为了使用概率分析，必须使用关于输入分布的知识或者对其做假设，然后分析算法，计算出一个期望的运行时间。

在这里插入图片描述
计算模型
在这里插入图片描述
在这里插入图片描述
雇佣情况分析
Events: E1, E2, …, En (事件)
Ei = we hire the i-th candidate(第i个受聘用)

指示变量Xi = I(Ei)

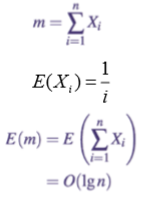
在这里插入图片描述
Assuming that the order in which the candidates are presented is a uniformly random permutation, the expected cost for hiring a new assistant out of n candidates is Θ(Ci⋅n + Ch⋅lg n)

一致性随机排练的生成
工具：随机数生成器 random(a,b)

方法1：排序法排列
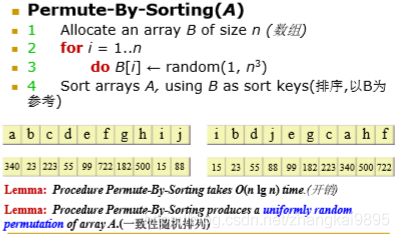
在这里插入图片描述
方法2：换位法排列
在这里插入图片描述

概率分析和随机算法
日积月累
06-06 587
本文以雇佣问题，生日悖论和球与箱子问题入手，着重讲述如何使用概率方法分析随机算法。
随机算法及其在雇佣问题中的应用及C代码示例
笔者从事电信媒体开发多年，愿意将多年的开发经验分享给同行
03-21 789
在计算机科学中，随机算法是指在算法的执行过程中使用随机选择或随机决策的算法。这种算法往往能够在平均情况下提供较好的性能，尽管在最坏情况下可能表现不佳。随机算法广泛应用于图论、排序、优化等领域，并在许多实际问题中取得了显著的效果。
第五章-概率分析和随机算法-5.1-雇用问题
Toby的博客
07-28 392
本文为《算法导论》5.1雇用问题的笔记，欢迎大家参考。
【算法】3 由招聘问题看随机算法
nomasp
05-29 5497
招聘问题我想看我博客的还是学生人群偏多吧，本身很快就要去面试了，在这篇博客的问题中，我们就把自己当作Boss过把瘾。某天，你想雇用一名算法工程师。当然，不可能让你这个Boss亲自去到处练习应聘者，而是选择了中介。雇用中介每天都会给你推荐一个应聘者（PS：还是让自己轻松点，一天只应聘一个人哈）。是个地球人都知道，你必须要给中介付一小笔钱。然后如果你雇用了一个应聘者则需要更多的钱，一来你要解雇现有的算法
算法导论 雇用问题的随机算法 PERMUTE-BY-SORTING（c语言）
almsch03的专栏
11-06 1834
算法导论中雇佣问题的随机算法，这个算法的过程是先取一个数组test_array，表示每个应聘者的id。然后取一个随机数组P，这个数组与test_array等长，随机数的范围是在0-n^3（n表示应聘者的个数）。这样取随机数是为了避免优先级的重复，即有很小的可能性取到相同的优先级。取出的随机数组表示test_array数组成员的优先级，依据此优先级来给test_array排序，这个过程就是PERMU
The on-line hiring problem
Andrewwiggin的博客
03-09 422
在这里插入图片描述 #include<stdio.h> int maxmum(int score[],int k,int n) { int bestscore=-100; for(i=0;i<k;i++) { if(score[i]>bestscore) bestscore=score[i]; } for(i=k;i<n;i++) { ...
随机算法之雇用问题
T的博客
10-02 771
问题描述： 假如你要雇用一个新的办公助理。你找了一个雇用代理，这个雇佣代理每天给你推荐一个应聘者。你面试这个人，决定是否录取他。你需要付的钱分为几部分：一部分给雇用代理,一部分用于雇用应聘者。 最近在学算法导论，这是第五章的内容。随机算法，我百度搜出来的解释是：“一个随机算法是一种算法，它采用了一定程度的随机性作为其逻辑的一部分。该算法通常使用均匀随机位作为辅助输入来指导自己的行为，超过随机位的所...
mysql 概率随机算法_概率分析与随机算法
weixin_32126843的博客
02-05 625
指示随机变量指示随机变量(indicator random variable，IRV)是概率分析中非常重要的一种离散随机变量，其用来表征某事件是否发生。更加具体的，假设事件A发生，变量IRV取值为1，否则取值为0. 数学上表述为： 指示随机变量是采用概率分析问题的一中基本手段。那么为什么要采用这种随机变量呢？首先：指示随机变量非常简单，对于任何概率问题都是可行的，并且该随机变量取值也比较简单。指示...
《算法导论》学习（六）----概率分析和随机算法
weixin_52042488的博客
09-02 1368
随机序列的生成算法 雇佣问题 概率分析 随机算法
【算法与招聘优化】基于概率分析的在线雇用问题研究：随机化算法与k值优化在人才选拔中的应用
最新发布
10-12
文章以概率分析为核心工具，系统讲解了在线雇佣问题的数学建模过程，重点介绍了预面试期参数k的确定方法及其对成功概率的影响，并通过数学推导得出k=n/e时最优的结论。结合随机化算法与Python代码实现，展示了完整的...
第五章 概率分析和随机算法 5.1 雇用问题
weixin_43172803的博客
07-28 704
5.1 雇用问题 一. 雇用问题 1. 问题描述   假设雇用一名新的办公助理，先找一名雇用代理。雇用代理每天推荐一个应聘者，雇用者决定是否雇用。雇用者必须给雇用代理一小笔费用，以便面试应聘者。在面试完每个应聘者后，如果该应聘者比目前的办公助理更合适，就会辞掉当前的办公助理，然后聘用新的。   HIRE-ASSISTANT 过程表示雇用策略。假设应聘办公助理的候选人编号为 111 到 nnn 。该过程中假设雇用者在面试完应聘者 iii 后，决定应聘者 iii 是否是你目前见过的最佳人选。初始化时，该过程创建
算法导论5.1 雇用问题
dianlu7964的博客
08-11 304
第五章围绕概率分析，随机算法，概率与期望展开了一系列有趣的讨论，其中许多有趣概率习题。------------------------------------------------------------------------------------------------------------------------------------------------ 雇佣问题描述...
Randomized algorithms(随机算法)
Melody_Gogo的博客
12-06 1222
随机算法是由一个雇佣问题引出的： 假如你要雇佣一名新的办公室助理，但是你先前的雇佣尝试都失败了，你打算找一个雇佣代理。雇佣代理每天给你推荐一个应聘者。你面试这个人，然后决定是否雇佣他，同时你需要付给雇佣代理一定的费用，以便面试应聘者。除此之外，雇佣一个人也需要花费一大笔钱，因为你必须辞掉目前的办公室助理，同时付给雇佣代理一大笔中介费。 你承诺：任何时候都找最合适的人来担任这项职务，因此你决定在面试完应聘者之后，如果该应聘者比目前的办公室助理更合适，就会辞掉当前的办公室助理，然后聘用新的。 同时你愿意为该策
【算法导论】雇佣问题
grefwfdxz
08-08 2521
首先介绍一点数学知识。 事件 A 的指示器随机变量I{A}I\{A\}I{A}定义为： I{A}={1如果A发生0如果A不发生 I\{A\} = \begin{cases} 1 \quad 如果A发生\\ 0 \quad 如果A不发生 \end{cases} I{A}={1如果A发生0如果A不发生​ 指示器随机变量的期望为： E[I{A}]=Pr{A}E[I\{A\}] = Pr\{A\}E[I{...
如何在面试中找到最优秀的候选人：雇佣问题的随机化算法探索
热门推荐
曾经“等你生日那天”都遥远得像未来，如今却可欢愉的挥手说“下个十年见”
07-01 7万+
本文探讨了雇佣问题及其解决方案中的随机化算法应用。雇佣问题要求在一系列不可回溯的面试中找到最优秀的候选人，传统贪心策略存在局限性。随机化算法通过随机排列和预面试期的引入，有效地提高了找到最佳候选人的概率。通过数学推导和实际模拟，我们验证了随机化算法在这一问题中的有效性，为面试和招聘过程中决策的优化提供了新的思路和方法。
算法导论第三版 第5章习题答案
DavidWang9527的专栏
11-05 5050
2020/11/04 初稿,主要加了Python实现。
算法导论第五章学习笔记
冰枫的随笔
04-27 1704
Probabilistic analysis We must use knowledge of, or make assumptionsabout, the distribution of inputs. The expectation is over this distribution. This technique requires that we can make a reasonable characterization of the input distribution.
求在线雇佣问题中最好雇佣者出现的概率及概率最大时最好雇佣者的位置
weixin_42022175的博客
05-24 1155
目录用蒙特卡罗算法模拟在线雇佣问题问题一 用蒙特卡罗算法模拟在线雇佣问题 问题一 最好的那个人出现的概率最大时 k 的取值和最大概率？ 在面试一个应聘者之后，我们能够给每人一个分数。在面试过j个人之后，我们知道这j个人中的最高分，但是不知道后面的n-j个会不会有最高的。所以我们决定采取下面的方法： 选择一个正整数k<n。面试然后拒绝前k个应聘者，再雇佣其后比前面的应聘者有更高分数的第一个应聘...
算法导论学习笔记——5.1雇佣问题（未完待续）
HDUCheater的博客
02-22 503
5.1雇佣问题 这章内容未编辑完 因为概率论没学，所以真的看不懂这类概率期望的问题QAQ 等到学完后回来完善 纯翻译代码 #include <bits/stdc++.h> using namespace std; typedef long long ll; const int inf = 0x3f3f3f3f; const int maxn=1000000; ll n,i,best,...
随机算法技术
06-17
### 随机算法技术的实现与应用 随机算法是一种利用随机性来解决问题的算法，其核心思想是通过引入随机数或概率分布来处理问题。随机算法在许多领域都有广泛的应用，例如优化问题、排序问题、数据抽取等。以下是随机算法的技术实现及其应用的相关内容。 #### 1. 随机算法的核心原理 随机算法的核心在于使用随机化机制来简化复杂问题的求解过程[^1]。这种机制可以通过生成随机数或随机选择来实现。例如，在遗传算法中，随机化种群、自然选择、交叉和变异等步骤均依赖于随机数生成器[^1]。此外，随机算法还能够通过概率分布描述随机过程的性质。 #### 2. 随机算法的实现方法 在实际开发中，随机算法通常基于编程语言提供的随机数生成库实现。例如，Python 的 `random` 模块提供了丰富的随机抽取方法[^3]。以下是一个简单的随机抽取代码示例： ```python import random # 定义一个列表 data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] # 随机抽取一个元素 random_element = random.choice(data) print("随机抽取的元素:", random_element) # 随机抽取多个元素 random_elements = random.sample(data, 3) print("随机抽取的多个元素:", random_elements) ``` 此外，随机算法还可以结合其他技术实现更复杂的任务。例如，随机油漆优化算法（SPO）是一种基于随机性的优化算法，其 Matlab 实现展示了如何通过随机搜索找到最优解[^4]。 #### 3. 随机算法的应用场景 随机算法在多个领域都有广泛应用。以下是一些典型的例子： - **雇佣问题中的期望计算**：在雇佣问题中，如果应聘者以随机顺序出现，则雇佣新办公室助理的期望次数为 $\ln n$[^2]。这一结果展示了随机算法如何通过概率分析解决实际问题。 - **快速排序的随机化实现**：随机化快速排序通过随机选择基准值来避免最坏情况的发生，从而提高算法的性能[^5]。以下是一个随机化快速排序的 C++ 实现： ```cpp #include <iostream> #include <cstdlib> #include <ctime> using namespace std; int Partition(int* ar, int left, int right) { srand(time(0)); // 初始化随机种子 int randIndex = left + rand() % (right - left + 1); // 随机选择基准值 swap(ar[randIndex], ar[left]); // 将随机选择的基准值放到首位 int tmp = ar[left]; while (left < right) { while (left < right && ar[right] > tmp) --right; ar[left] = ar[right]; while (left < right && ar[left] <= tmp) ++left; ar[right] = ar[left]; } ar[left] = tmp; return left; } void QuickSort(int* ar, int left, int right) { if (left < right) { int pos = Partition(ar, left, right); QuickSort(ar, left, pos - 1); QuickSort(ar, pos + 1, right); } } int main() { int ar[] = {56, 12, 89, 90, 23, 34, 100, 56, 45, 78, 67}; int n = sizeof(ar) / sizeof(ar[0]); for (auto& x : ar) cout << x << " "; cout << endl; QuickSort(ar, 0, n - 1); for (auto& x : ar) cout << x << " "; return 0; } ``` - **数据抽取与验证码生成**：在日常开发中，随机算法常用于数据抽取和验证码生成等任务[^3]。例如，生成一个六位数字验证码可以使用以下 Python 代码： ```python import random def generate_captcha(length=6): captcha = "" for _ in range(length): captcha += str(random.randint(0, 9)) return captcha print("生成的验证码:", generate_captcha()) ``` #### 4. 随机算法的优势与局限性 随机算法的主要优势在于其能够在不确定性和复杂性较高的环境中提供高效解决方案。然而，随机算法也存在一定的局限性，例如结果的不可预测性和对随机数生成器质量的依赖。 --- ###
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值