介绍:
回归:用一条直线对已知数据点进行拟合的过程称作回归。
利用Logistic回归进行分类的主要思想:根据现有数据对分类边界线建立回归公式,以此进行分类。
回归的关键在于寻找最佳拟合参数,使用的是最优化算法。
Logistic回归的一般过程:
1 收集数据---2 准备数据---3 分析数据---4 训练算法(目的是找到最佳的分类回归系数,占用大部分时间)---5 测试算法
---6 使用算法(将数据转换为对应的结构化数值,基于训练得到的回归系数进行简单的回归计算,并判断类别)
5.1 基于Logistic回归和Sigmoid函数的分类
期待的函数:根据所有的输入然后预测出类别。若有两个分类,则输出为0/1.
单位阶跃函数:该函数在跳跃点上从0瞬间跳到1,该过程有时很难处理。

Sigmoid函数:有单位阶跃函数相似的性质,且在数学上更易处理。
计算公式和函数图像如下:


当x为0时,函数值为0.5。随着x值的增大,函数值将逼近于1。随着x的减小,函数值将逼近于0.Logistic回归分类器:在每个特征上都乘以一个回归系数,然后把所有的结果值相加,将这个总和带入到Sigmoid函数中,进而得到一个范围在0-1之间的数值。任何大于0.5的数据被分入1类,小于0.5被归入0类。
z=w0x0+w1x1+w2x2+...+wn
5.2 基于最优化方法的最佳回归系数确定
此处涉及到的最优化方法:梯度上升法,随机梯度上升法,改进的随机梯度上升法
5.2.1 梯度上升法
思想:要找到某个函数的最大值,最好的方法是沿着该函数的梯度方向探寻。
如果梯度记为∇∇,则函数f(x,y)的梯度由下式表示:
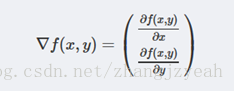
这个梯度意味着沿xx方向移动∂f(x,y)∂x∂f(x,y)∂x,沿yy方向移动∂f(x,y)∂y∂f(x,y)∂y。且函数f(x,y)f(x,y)在待计算的点上有定义且可微。
增加步长(移动量的大小)后,迭代公式为:w:=w+α∇wf(w)
迭代结束条件:比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围。
伪代码:
每个回归系数初始化为1
重复R次:
计算整个数据集的梯度
使用alpha*gradient更新回归系数的向量
返回回归系数
代码
#sigMiod函数
def sigmoid(inX):
return 1 / (1 + exp(-inX))
#梯度上升法算法
def gradAscent(dataMatIn, classLabels):
#将列表形式的特征数据转化为矩阵形式,方便计算:(100,3)
dataMatrix = mat(dataMatIn)
#将列表形式的标签转化为矩阵形式,1行多列。然后通过转置,转化为列向量,方便计算:(100,1)
labelMat = mat(classLabels).transpose()
#print(shape(labelMat))
m, n = shape(dataMatrix)#分别获得特征矩阵的行数和列数
alpha = 0.001 #设置移动步长
maxCycles = 500#设置迭代次数
weights = ones((n,1))#初始化回归系数均为1,n个特征1列
#print(shape(weights))
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights)#计算每个样本乘以回归系数后得到的值,调用sigmoid函数,获得分类值,是一个列向量
#print(dataMatrix * weights)
#print(h)
error = labelMat - h#获得sigmoid分类结果和真实结果间的差值
#print(error)
#更行回归系数,按照差值的方向调整回归系数?不明白
weights = weights + alpha * dataMatrix.transpose() * error
return weights
5.2.2 随机梯度上升
由于梯度上升算法更新回归系数时需要遍历整个数据集(计算整个数据集的分类和更新回归系数),计算复杂度太高。所以随机梯度上升算法(一次仅用一个样本点来更新回归系数)对其进行了改进。
随机梯度上升算法可以在每个新样本到来时对分类器进行增量式更新,因而是一个在线学习算法,一次处理所有数据被称为‘批处理’。
伪代码:
所有回归系数初始化为1
对数据集中每个样本:
计算发样本的梯度
使用alpha * gradient更新回归系数值
返回回归系数值
代码:
#随机梯度上升算法
def stocGradAscent0(dataMatrix, classLabels):
m, n = shape(dataMatrix)#分别获得特征矩阵的行数和列数
alpha = 0.001 #设置移动步长
weights = ones(n)#初始化权重,为numpy.ndarray类型
for i in range(m):
h = sigmoid(sum(dataMatrix[i] * weights))#[a,b]*[c,d]=[ab,cd]
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights
参数变化情况:
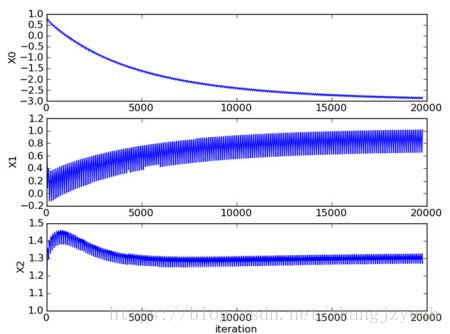
从上图中可以看出,不同系数需要经过不同的迭代次数才能达到稳定的状态,且在大的波动停止之后还有一些小的周启新那个波动,这可能是因为一些为被正确分类样本点数据,在每次迭代时会引发系数的剧烈改变。我们期望算法能避免来回波动,从而收敛到某个值,且收敛速度需要加快。因此下面一部分解决了该问题。
5.2.3 随机梯度上升算法的改进
代码:
'''
函数功能:根据特征,标签获得回归系数
输入:特征数据,标签数据,迭代次数
输出:回归系数
思想:调整每次迭代时的步长,且步长随着迭代次数不断减少,但不会减少到0(确保多次迭代之后新数据仍具有一定的影响)
可避免步长的严格下降:alpha每次减少1/(i+j),i为样本点下标,j为迭代次数。当j<max(i),alpha就不是严格下降的
可通过随机选择样本来更新回归系数,将减少周期性的波动。
可指定迭代次数,默认为150次
'''
def stocGradAscent1(dataMatrix, classLabels, numIter = 150):
m,n = shape(dataMatrix)#获取样本行数和特征个数
weights = ones(n)#初始化回归系数
#进行多次迭代
for j in range(numIter):
dataIndex = list(range(m))#定义0-行数的随机序列,用于对样本进行随机选择
#根据随机的样本,更新回归系数
for i in range(m):
alpha = 4 / (1.0 + j + i) + 0.01#步长在每次迭代时需要调整
randIndex = int(random.uniform(0, len(dataIndex)))#获得随机样本的位置
h = sigmoid(sum(dataMatrix[randIndex] * weights))#计算随机样本的分类结果
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]#更新回归系数
del(dataIndex[randIndex])#删除此样本的位置,避免重复选择
return weights
参数变化情况:
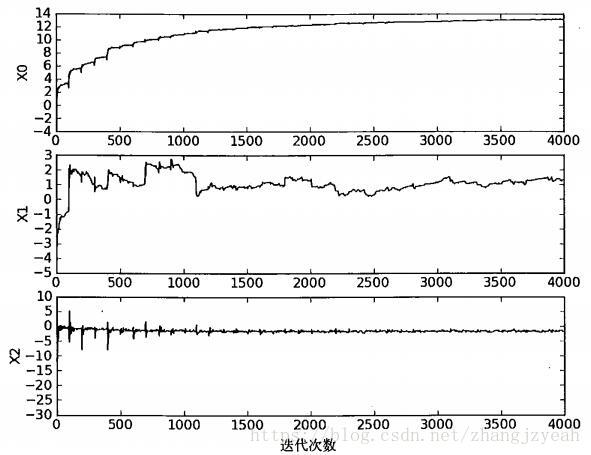
可以看到,收敛速度比固定alpha更快,没有出现周期性波动(随机选择机制?)





 本文介绍了Logistic回归的基础概念和应用,重点讲述了如何使用Sigmoid函数进行分类。通过梯度上升法、随机梯度上升及其改进版来确定最佳回归系数,以实现高效分类。详细阐述了各个算法的原理、伪代码和参数变化情况。
本文介绍了Logistic回归的基础概念和应用,重点讲述了如何使用Sigmoid函数进行分类。通过梯度上升法、随机梯度上升及其改进版来确定最佳回归系数,以实现高效分类。详细阐述了各个算法的原理、伪代码和参数变化情况。
















 1156
1156

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








