移动流行区间法（MEM）的原理和与LSTM、ARIMA等时间序列方法的区别

原创已于 2025-10-31 11:35:05 修改 · 921 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#lstm #人工智能 #rnn

于 2025-10-31 11:00:44 首次发布

原理

移动流行区间法（MEM）是一种基于历史流行病学数据，通过统计模型来定量界定疾病流行阈值、识别流行开始和评估流行强度的监测预警方法。下面这个流程图可以帮助你直观地把握MEM的核心步骤与逻辑：

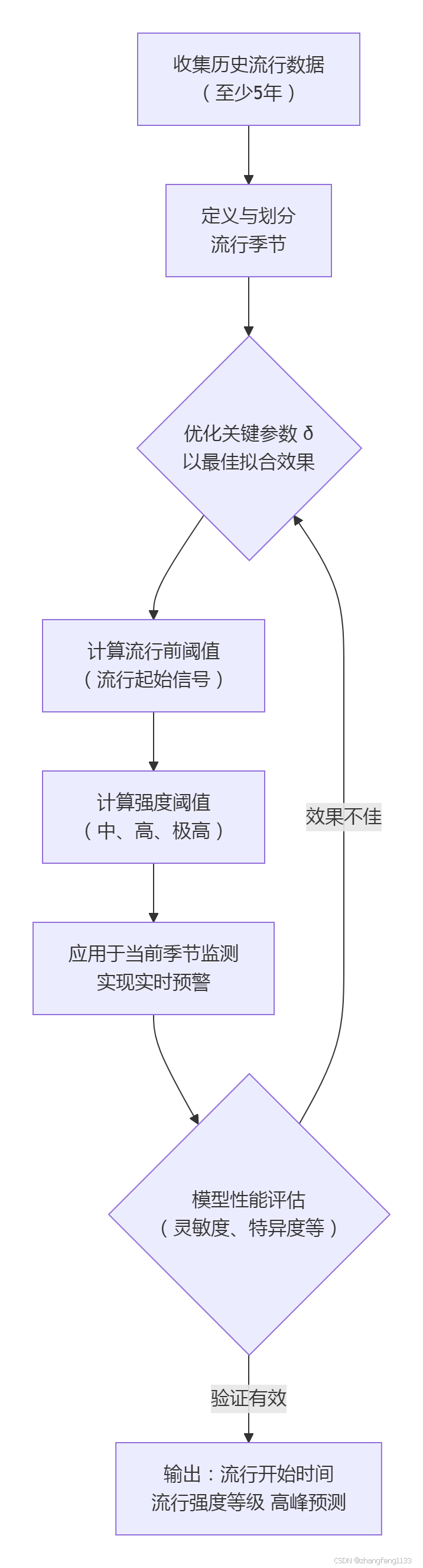
在这里插入图片描述

下面我们来具体看看它的核心思想和关键步骤。

💡 核心思想与关键步骤

MEM的基本思路是，一个疾病的流行在历史上遵循一定的季节性规律。MEM通过分析过去若干年（通常建议至少5年）的周度监测数据（如流感样病例百分比、手足口病周发病率等），来设定一个客观的“阈值”，当当前周期的数据超过这个阈值时，就认为流行开始了。它还能进一步设定不同水平的阈值，用以评估流行的严重程度（如中等、高、极高）。

其具体实施通常包含以下几个关键步骤：

数据准备与流行季定义：首先需要收集足够长时间跨度的历史周数据。然后，需要明确每年流行季的时间范围（例如，流感可能定义为第40周至次年第20周），并将每个流行季划分为流行前期、流行期和流行后期三个阶段。
关键参数δ的优化：参数δ是MEM模型中的一个核心参数，用于确定流行开始和结束的判定标准，通常取值范围在2.0-4.0之间。通过交叉验证，选择使得模型评估指标（如灵敏度、特异度、约登指数等）最优的δ值。
计算流行阈值：
◦ 流行前阈值（流行起始信号）：汇总所有历史流行季中“流行前期”和“流行后期”里发病率最高的若干周次的数据，计算其平均值的单侧95%置信区间上限。当当前监测值超过此阈值，提示流行可能开始。

◦ 强度阈值（中、高、极高）：取每个历史流行季的“流行期”内发病率最高的若干周次的数据，计算其几何平均值的特定百分位数（如40%、90%、97.5%）置信区间上限，分别作为中等、高和极高流行强度的阈值。
模型验证与应用：使用历史数据对建立的MEM模型进行交叉验证，评估其识别流行期的准确性。验证通过的模型即可用于当前季节的实时监测和预警。

🎯 方法特点与优势

MEM方法的主要优势在于：
• 客观透明：基于历史数据和明确的统计标准设定阈值，减少了主观判断的影响。

• 功能综合：不仅能判断流行起始，还能评估流行强度，甚至可用于预测流行高峰（例如，通过计算从超过流行阈值到达到历史高峰的平均周数来预测当前流行季的高峰时间）。

• 灵活性：可通过调整参数δ或对特殊流行模式（如双峰流行）进行数据分割处理，以适应不同地区和疾病的特异性。例如，广东省的研究就针对手足口病存在夏季和秋季两个流行高峰的特点，将流行季拆分为两部分分别建立MEM模型，取得了良好效果。

• 良好的预警性能：在多项应用于流感和手足口病的研究中，MEM模型均显示出较高的灵敏度和特异度（多数在80%甚至90%以上）

移动流行区间法”(Moving Epidemic Method，简称 MEM) 是一种完全基于历史监测数据、无需外部协变量的时间序列建模技术，用于为季节性传染病划定“流行阈值”和分级强度阈值，进而判断当前季节是否进入流行期及其强度等级。其核心思路与操作步骤如下：

原理
将多年同-周(或同-月)的发病率(或阳性率)视为一条“参考曲线”。
对每一年曲线做标准化处理，使曲线下面积(AUC)相等，消除年度间绝对水平差异。
在所有年份的标准化曲线上，对每个时间单位(周)计算分位数(通常取 40%–60% 作为“核心流行带”)，形成一条“流行性区间”。
用这条区间去切割当前季节的观测曲线：首次持续高于上限即判定为“流行开始”，跌回上限以下且保持数周视为“流行结束”。
通过改变分位数可得到不同强度等级(低、中、高、极高)的阈值，实现分级预警。
主要输出
流行阈值(Epidemic threshold)：区分“非流行/流行”的临界值。
强度阈值(Intensity thresholds)：低、中、高、极高等多级警戒线。
时间参数：季节起始周、结束周、峰值周及峰值大小。
应用示例
在西南三省(四川、贵州、云南)流感监测中，MEM 以 2010–2017 年周阳性率建模，得出各省流行阈值分别为 15.49%、12.13%、6.40%，并验证了 2017–2018 季节的实际流行强度。
研究显示四川、贵州呈明显双峰型流行，云南则为单峰；模型约登指数 0.57–0.76，表明判定效果良好，可用于省级实时预警。
优点
仅依赖历史监测数据，无需气温、搜索指数等外部变量，便于基层推广。
可同时给出“是否流行”和“强度等级”双重信息，支持精准响应。
模型参数自动由数据驱动，减少主观设定。
局限与注意事项
需要 ≥3–5 个完整季节的高质量连续数据，初期数据不足时稳定性差。
对报告滞后、检测策略变动敏感，需先做数据同质性校正。
只适用于有明显季节性的疾病；非季节或亚季节性传播场景需改用其他模型。
简言之，移动流行区间法通过“让历史数据自己告诉未来”的方式，为流感等季节性传染病提供了一条简单、透明、可自动运行的预警分界线，已被欧盟 ECDC 及多国流感中心采纳，也可供其他具有季节性规律的传染病参考使用。

移动流行区间法（MEM）的数学核心在于，它基于历史数据，通过统计方法确定一个阈值，当当前监测值超过这个阈值时，就认为疾病流行开始了。其数学模型可以看作是一种特殊的广义线性模型或基于似然的方法，核心是建立发病率的时间序列模型并计算流行病学阈值。

以下是MEM模型中涉及的主要数学公式和概念，采用类似优快云技术博客的格式呈现。

核心思想：最大熵原理与模型构建

MEM的底层思想与最大熵原理有相通之处。该原理认为，在所有满足已知约束条件的概率模型中，熵最大的模型是最优的，因为它没有引入任何未知的偏差。

在MEM的语境下，可以理解为：在已知历史流行季的基线数据（约束条件）下，我们选择的流行阈值模型，应该是对“非流行期”数据最无偏、最不确定（熵最大）的模型，从而确保只有真正显著的升高才会触发预警。

最终得到的模型条件概率分布形式为：
[ P(\text{流行状态} | \text{时间}t, \text{历史数据}) \propto \exp\left(\sum_{i=1}^{n} \lambda_i f_i(t, \text{历史数据})\right) ]
其中， f_i 是特征函数（例如，t周的发病率是否显著高于历史同期）， \lambda_i 是相应的权重参数。这个形式保证了在给定约束下熵最大。

关键参数：δ (delta) 的优化

参数 δ 是MEM模型中的核心参数，它是一个乘数，用于调整计算阈值时所使用的置信区间的宽度，直接影响流行起始和结束判定的灵敏度。其取值范围通常在 2.0 到 4.0 之间。

最优δ值通过交叉验证确定，目标是使模型的综合评估指标最优。常用的评估指标包括：

• 灵敏度（Sensitivity）: \text{Sensitivity} = \frac{TP}{TP + FN}

• 特异度（Specificity）: \text{Specificity} = \frac{TN}{TN + FP}

• 约登指数（Youden’s Index）: J = \text{Sensitivity} + \text{Specificity} - 1

其中，TP（真阳性）、FN（假阴性）、TN（真阴性）、FP（假阳性）是基于历史数据验证的判别结果。优化过程就是寻找使得约登指数或其他预定目标函数最大的δ值。

流行阈值的计算

a) 流行前阈值（流行起始信号）

此阈值用于判断流行是否开始。它基于所有历史流行季中“流行前期”和“流行后期”的数据计算。

计算基线值：从每个历史年份的“流行前期”和“流行后期”中，选取发病率最高的M周（例如，M=3）的数据，计算其平均值。
计算流行前阈值：
$KaTeX parse error: Undefined control sequence: \[ at position 2: \̲[̲ \text{流行病学阈值} …$

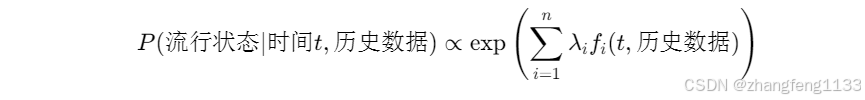
更精确的算法是计算这些基线值平均值的单侧95%置信区间上限（Upper Confidence Limit, UCL），其中δ值决定了置信区间的宽度（例如，δ=2.5对应大约95%置信水平）。

b) 强度阈值（中、高、极高）

这些阈值用于评估流行期间的严重程度。它们基于各历史流行季“流行期”内发病率最高的N周（例如，N=5）的数据计算。

计算几何均值：对每个流行季，计算其流行高峰阶段数据的几何平均数。
$KaTeX parse error: Undefined control sequence: \[ at position 2: \̲[̲ \text{几何平均数} =…$

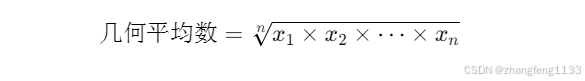
几何平均数受极端值影响小，更适合偏态分布的数据。
计算百分位数：计算所有历史流行季上述几何平均数的特定百分位数（例如，40%、90%、97.5%）。
确定强度阈值：
$KaTeX parse error: Undefined control sequence: \[ at position 2: \̲[̲ \text{中等强度阈值} …$
在实际应用中，同样会使用δ参数调整的UCL方法来确定最终的阈值。
与时间序列模型的联系

MEM可以看作是基于历史时间序列数据建立的一个非线性谱估计模型。其功率谱估值的表达式为：
$ $KaTeX parse error: Undefined control sequence: \[ at position 2: \̲[̲ P(f) = \frac{P…$ $
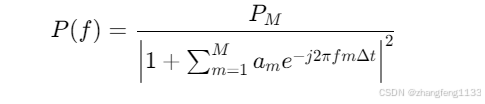
在这里插入图片描述

其中， P_M 是预测误差滤波器的输出功率， a_m 是模型参数，由已知的自相关函数值决定。这个公式反映了MEM与自回归（AR）模型在本质上的等价性，即MEM可以视为一个试图拟合疾病发病率序列内在规律的AR模型。

移动流行区间法（MEM）与LSTM、ARIMA等时间序列方法在核心原理、应用场景和技术特点上存在显著差异。下面我将从多个维度对它们进行系统比较，并使用表格概括主要区别。

比较维度移动流行区间法 (MEM) LSTM (长短期记忆网络) ARIMA (自回归综合移动平均模型)

核心原理基于历史流行曲线设定流行病学阈值，识别流行起始点和强度等级使用门控机制（遗忘门、输入门、输出门）的循环神经网络，学习序列中的长期依赖关系结合自回归(AR)、差分(I)和移动平均(MA) ，对平稳时间序列进行建模和预测

应用场景专用于疾病监测预警，如流感、手足口病的流行期判断和强度分级通用序列建模，如时间序列分类/预测、自然语言处理、语音识别等适用于平稳时间序列预测，如销售量、市场规模等

数据要求依赖历史流行病学数据（如周发病率、病毒阳性率），需一定年份的基线数据需要大量数据进行训练，对数据平稳性要求不高要求数据平稳（均值、方差恒定），非平稳数据需差分处理

模型输出输出流行阈值和强度等级（如中等、高、极高），提供定性预警信号输出具体的预测值（如未来病例数、分类概率），为定量预测输出未来时间点的数值预测，为定量预测

处理长期依赖能力基于季节性规律，能有效捕捉年度或季节性周期的流行模式通过细胞状态和门控机制专门设计用于捕捉长期依赖，理论上可处理非常长的序列对长期依赖的捕捉能力相对有限，更依赖近期数据和明显的周期模式

模型复杂性与解释性模型相对简单，参数较少（如δ值），结果易于流行病学解释模型复杂，参数多，是典型的"黑箱"模型，解释性较差模型结构清晰，参数（p,d,q）有统计意义，解释性介于MEM和LSTM之间

计算效率计算高效，通常基于历史数据直接计算阈值，无需复杂迭代训练计算量大，耗时较长，且难以并行处理长序列参数估计（如最大似然估计）计算量相对适中，优于LSTM但可能不如MEM

💡 方法选择建议

• MEM：当你的目标是对特定疾病的流行态势进行定性预警和等级划分，并且拥有较为规整的历史监测数据时，MEM是直接且高效的工具。它在公共卫生领域的疾病防控决策中能提供直观的参考依据。

• LSTM：适用于数据量巨大、模式复杂且需要捕捉长期依赖关系的预测任务。例如，如果你需要基于多维度、长时间序列的数据进行非常精准的病例数预测，且计算资源充足，LSTM或其变体（如GRU）是强大的选择。

• ARIMA：适用于相对平稳、模式不过于复杂的时间序列预测。当数据具有明显的趋势或季节性，且经过差分等处理后可转化为平稳序列时，ARIMA是一个可靠且解释性较好的基准模型。