林轩田机器学习基石笔记（第8节）——PLA循环停止条件的探讨

引言

第7节我们讨论了如何找到一条线把所有的圈圈叉叉都分在不同的两边，但是其实有一个隐含的大前提，那就是圈圈叉叉的分布必须是线性可分的，如下第1张图。如果是线性不可分那么，如下第2、3张图是无法用PLA算法把圈圈叉叉分开的。

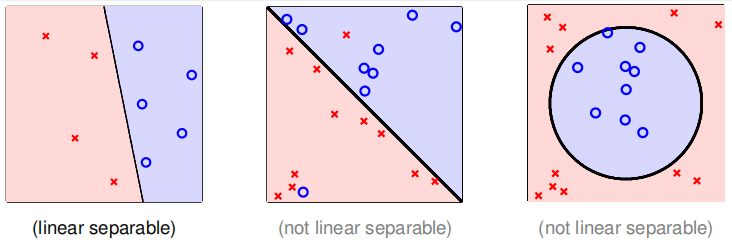
本节课我们就讨论在线性可分的前提之下，PLA循环什么时候才能终止。

初步论证

我们知道，如果$y_{n(t)} \neq sign(W_t^TX_{n(t)})$，那么代表$W$这条向量不符合我们的要求，那么如果现在出现一条这样的线$y_n = sign(W_f^TX_n)$，那么就说明我们已经找到一条合适的线了，这条线把所有的圈圈叉叉都分在了不同的两边。据此，我们可以做一个推论：平面上的任何圈圈或者叉叉的点到这条线的最小距离都大于0，即 min $y_n W_f^TX_n>0$。亦可以推论，任何一个之前犯错误的圈圈或叉叉到这条线的距离也大于0，且大于等于最小距离，即 $y_{n(t)} W_f^TX_{n(t)} \geq$ min $y_n W_f^TX_n>0$。

那现在我们要做一件事情，那就是我们找到的这条线Wt是否接近于我们想要的Wf。这里有一个数学知识，那就是衡量两个向量是否接近，就要把这两个向量做内积，内积越大说明越接近。

那么我们只要证明$W_f^TW_{(t+1)}$大于$W_f^TW_t$就好了！在第7节，我们知道$W_{(t+1)}$其实就是$W(t)+yX$，如下图：

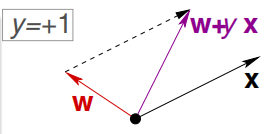
于是有如下推导：
$W_f^TW_{(t+1)} = W_f^T(W_t+y_{n(t)}X_{n(t)})$

又因为$y_{n(t)} W_f^TX_{n(t)} \geq$ min $y_n W_f^TX_n>0$，所以代入以上式子得$W_f^TW_{(t+1)} \geq W_f^TW_t+$min$y_n W_f^TX_n$

又因为 min $y_n W_f^TX_n>0$，所以存在$W_f^TW_{(t+1)} > W_f^TW_t+0$，得证：$W_f^TW_{(t+1)} > W_f^TW_t$

完整流程如下：

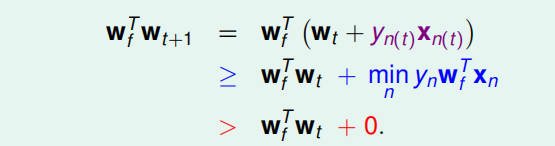
上面的论证还有问题，进一步论证

虽然我们证明了$W_f^TW_{(t+1)} > W_f^TW_t$，说明了$W_t$和$W_f$的内积的确越来越大，说明两者越来越接近。但是这里我们并没有考虑向量长度的问题，如果两者长度很长，内积也会很大，所以接下来我们还要继续证明。

在第7节中，当我们找到一条错误的点X(即$y_{n(t)} \neq sign(W_t^TX_{n(t)})$)，我们就会旋转更新$W$的角度，说明这个点到分割线的距离小于0，即

现在我们试着找到$W_t$和$W_{t+1}$之间的关系，首先我们队$W_{t+1}$的绝对值（即长度）进行平方，根据下图：

我们知道$W_{t+1}=W+yX$，那么可以推断$|W_{t+1}|^2=|W_t+y_{n(t)}X_{n(t)}|^2$，接着式子又可以转化为

$|W_{t+1}|^2=|W_t|^2+2y_{n(t)}W_t^TX_{n(t)}+|y_{n(t)}X_{n(t)}|^2$，又因为$y_{n(t)} W_f^TX_{n(t)} \leq 0$，

所以有$|W_{t+1}|^2 \leq |W_t|^2+0+|y_{n(t)}X_{n(t)}|^2$. 这说明$W_t$的成长与中间的$y_{n(t)} W_f^TX_{n(t)}$没有太大关系，

而是靠$|y_{n(t)}X_{n(t)}|^2$成长。而$|y_{n(t)}X_{n(t)}|^2$表示任意犯错误的点，所以我们只要找到最远的一个点进行讨论，

即$|W_{t+1}|^2 \leq |W_t|^2+$max$|y_{n(t)}X_{n(t)}|^2$。又因为$y_n$是+1或-1，平方后没有差别。所以完整过程如下：

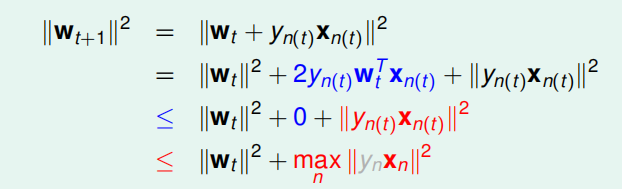
结论

前面我们证明了$W_t$和$W_{t+1}$的内积会越来越大，现在我们又证明了$W_t$每次最多长 max$|y_{n(t)}X_{n(t)}|^2$，

$W_t$会慢慢的长。而两个向量的内积不可能无限的长，最大值只能为1，所以说明循环最终会停下来。他们的关系如下：

即，从$W_0$开始，经过 $T$ 次更新后，对 $W_f$ 和 $W_t$ 进行正规化向量，并进行内积操作，最终的结果大于等于$\sqrt T \cdot constant$，其中$\sqrt T$代表更新次数的根号，$constant$是一个常数。

这里涉及到一个数学概念正规化向量，定义如下：

写到这里我懵逼了，但是不管怎么样这一节就是为了证明一点：PLA算法最终会停下来！

===========================懵逼分割线===========================

欢迎大家加入Q群讨论：463255841

===========================懵逼分割线===========================