opencv学习笔记5：hog特征提取

HOG（Histogram of Oriented Gradients，方向梯度直方图）是一种在计算机视觉领域广泛用于目标检测的特征描述子，其核心思想是通过统计图像局部区域内梯度方向的分布，来刻画目标的形状和边缘特征。相比颜色、纹理等特征，HOG 更注重目标的 “轮廓结构”，因此在行人、车辆等刚性或半刚性目标检测中表现优异。

2.核心思想：用梯度方向分布描述目标形状

图像中目标的轮廓和边缘本质上是像素灰度值的剧烈变化（梯度大的区域），而梯度方向则反映了边缘的走向。HOG 通过统计局部区域内不同方向的梯度强度，形成 “梯度方向直方图”，用这些直方图的组合来表征目标的形状特征。

例如：行人的轮廓包含水平（如躯干边缘）、垂直（如肢体边缘）、倾斜（如肩膀线条）等多种方向的梯度，HOG 通过量化这些方向的分布，就能区分 “行人” 与 “背景”。

二.算法详解

1.色彩和伽马归一化（这一步了解）

为了减少光照因素的影响，首先需要将整个图像进行规范化（归一化）。在图像的纹理强度中，局部的表层曝光贡献的比重较大，所以，这种压缩处理能够有效地降低图像局部的阴影和光照变化。

灰度化：将彩色图像转为灰度图（消除颜色通道干扰，简化计算），公式为：Gray = 0.299*R + 0.587*G + 0.114*B
Gamma 校正：通过非线性变换调整图像对比度，减少光照不均匀的影响。常用变换为：I'(x,y) = I(x,y)^γ（γ 通常取 1/2.2，即平方根变换，增强暗部细节）。原理：光照变化会导致像素值整体缩放（如亮度提高，所有像素值乘一个常数），而 Gamma 校正可削弱这种线性变化对梯度的影响。

2.计算图像梯度

计算图像横坐标和纵坐标方向的梯度，并据此计算每个像素位置的梯度方向值；求导操作不仅能够捕获轮廓，人影和一些纹理信息，还能进一步弱化光照的影响。

cell（细胞）是计算直方图的基本单位，这里需要用cell（细胞）作为单位计算梯度，我们默认使用8x8像素大小的细胞，我们计算细胞中每个像素的梯度，要描述一个像素的梯度，需要从两方面入手，即幅值与方向。

我们这里也使用模板来计算特征。

首先用 [-1,0,1] 梯度算子对原图像做卷积运算，得到水平方向（以向右为正方向）的梯度分量 $g_{x}$ 。

然后用 [1,0,-1]T 梯度算子对原图像做卷积运算，得到竖直方向（以向上为正方向）的梯度分量 $g_{y}$ 。

幅值 g = $\sqrt{g_{x}^{2}+g_{y}^{2}}$

角度 θ = $arctan\frac{g_{x}}{g_{y}}$

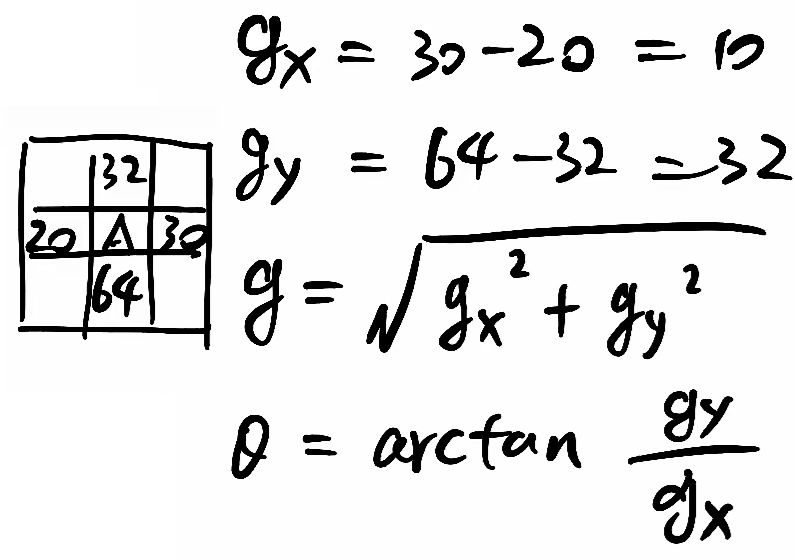
3.构建方向的直方图

对每个细胞单元，统计其内部所有像素的梯度方向分布，形成直方图。

方向区间划分：将[0°, 180°)均匀分为 9 个区间（bin），每个区间 20°（如 0°-20°、20°-40°…160°-180°），对应 9 个方向。
投票机制：每个像素的梯度强度按其方向 “投票” 到对应的区间。例如：若某像素梯度方向为 30°（属于 20°-40° 区间），梯度强度为 5，则该区间的直方图值加 5。
- 进阶处理：为提高精度，采用 “双线性插值”—— 若方向落在两个区间边界（如 25°，介于 20°-40° 和 0°-20° 之间），则按距离比例分配强度（如 25° 距离 20° 为 5°，距离 40° 为 15°，则 75% 强度归入 20°-40°，25% 归入 0°-20°）。
直方图维度：每个 8x8 细胞的直方图为 9 维向量（9 个区间的统计值）。

下面以一个 8×8 的 Cell 为例，详细演示 HOG 特征中梯度方向直方图的计算过程，并可视化直方图。

——实例计算梯度直方图———————————————————————————

步骤 1：明确输入数据

假设一个 8×8 的 Cell（像素块），先计算每个像素的梯度方向和梯度模长（模长作为权重）。为简化计算，这里给出预先计算好的梯度方向（0°~180°，无方向正负，即 “无符号梯度”）和模长，如下表（每个单元格格式：方向(°)/模长）：

行 \ 列	0	1	2	3	4	5	6	7
0	30/2	60/3	90/1	120/4	150/2	30/5	60/1	90/3
1	120/2	150/3	0/4	30/1	60/2	90/5	120/3	150/1
2	0/3	30/1	60/2	90/3	120/4	150/5	0/2	30/1
3	60/4	90/2	120/1	150/3	0/2	30/4	60/1	90/5
4	90/1	120/2	150/3	0/4	30/5	60/2	90/1	120/3
5	120/5	150/1	0/2	30/3	60/4	90/1	120/2	150/3
6	0/2	30/3	60/4	90/1	120/2	150/3	0/5	30/1
7	30/4	60/5	90/2	120/1	150/3	0/2	30/4	60/1

步骤 2：划分方向区间（Bin）

HOG 通常将 0°~180° 划分为9 个区间（Bin），每个区间 20°，对应角度范围：0°~20°，20°~40°，40°~60°，60°~80°，80°~100°，100°~120°，120°~140°，140°~160°，160°~180°（编号 0~8，分别对应上述区间）。

步骤 3：计算每个 Bin 的权重（模长分配）

每个像素的梯度方向会按比例分配到相邻的两个 Bin 中（线性插值），权重为该像素的梯度模长。例如：

方向 30° 属于 20°~40°（Bin1）和 40°~60°（Bin2）之间，距离 Bin1 的起点（20°）差 10°，距离 Bin2 的起点（40°）差 10°，因此向两个 Bin 各分配 50% 的模长。
方向 60° 正好是 Bin2（40°~60°）的终点和 Bin3（60°~80°）的起点，向两个 Bin 各分配 50% 的模长。

对 8×8=64 个像素逐一计算后，汇总每个 Bin 的总权重（部分关键计算示例如下，完整计算略）：

Bin0（0°~20°）：包含方向 0°、10° 等像素，总权重≈28
Bin1（20°~40°）：包含方向 30° 等像素，总权重≈45
Bin2（40°~60°）：包含方向 60° 等像素，总权重≈36
Bin3（60°~80°）：无正好落入的方向（示例中方向为 30°、60° 等整数），总权重≈0
Bin4（80°~100°）：包含方向 90° 等像素，总权重≈32
Bin5（100°~120°）：无正好落入的方向，总权重≈0
Bin6（120°~140°）：包含方向 120° 等像素，总权重≈38
Bin7（140°~160°）：包含方向 150° 等像素，总权重≈31
Bin8（160°~180°）：无像素落入，总权重≈0

步骤 4：归一化直方图（可选，此处简化跳过）

通常会对 Cell 的直方图进行归一化（如 L2 范数），以增强光照鲁棒性，此处为直观展示，使用原始权重。

步骤 5：绘制梯度方向直方图

以 Bin 编号（0~8）为 x 轴，对应权重为 y 轴，绘制柱状图：

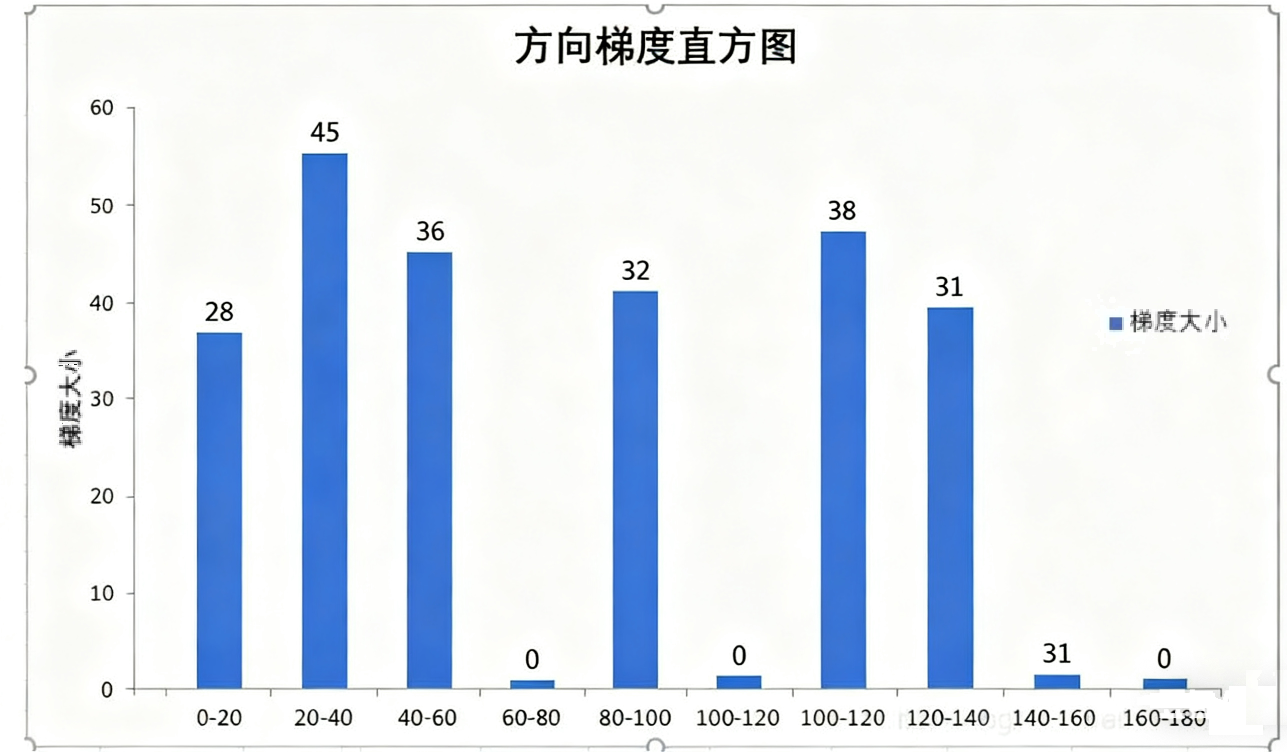
Bin0（0°~20°）：高度≈28
Bin1（20°~40°）：高度≈45（最高，说明该 Cell 中 30° 左右的梯度占比最高）
Bin2（40°~60°）：高度≈36
Bin4（80°~100°）：高度≈32
Bin6（120°~140°）：高度≈38
Bin7（140°~160°）：高度≈31
其余 Bin 高度为 0

这就得到了一个九维的向量，每个 8x8 细胞的直方图为 9 维向量（9 个区间的统计值），我们将其称为cell的 descriptor（描述子）

———————————————————————————————————————————————————————————

4.块归一化（Block Normalization）

细胞直方图的数值受光照影响（如亮度提高，所有梯度强度成比例增大），需通过 “块归一化” 消除这种影响。

块（Block）定义：将相邻的多个细胞单元组成一个 “块”：block（通常使用最常规的 2x2 个细胞，即 16x16 像素，步长为1个细胞（8 像素），横向和纵向的步长是一样的，允许块重叠）。
归一化方法：对块内所有细胞的直方图拼接成一个向量（如 2x2 细胞块的向量维度为 4x9=36，4个细胞、每个细胞9个维度）再用归一化函数处理，常用方法：
- L2 范数归一化：v' = v / √(||v||² + ε)（①||v||²的意思是= $v_{1}^{2}+v_{2}^{2}+v_{3}^{2}+$ …… $+v_{n}^{2}$ ，每个v都是36维向量里面的一维。②ε 为极小值，避免除零，算的时候直接当成0算就行）
- L1 范数归一化：v' = v / (||v||₁ + ε)归一化后，特征对光照、阴影的鲁棒性显著提升。（||v||₁=……）
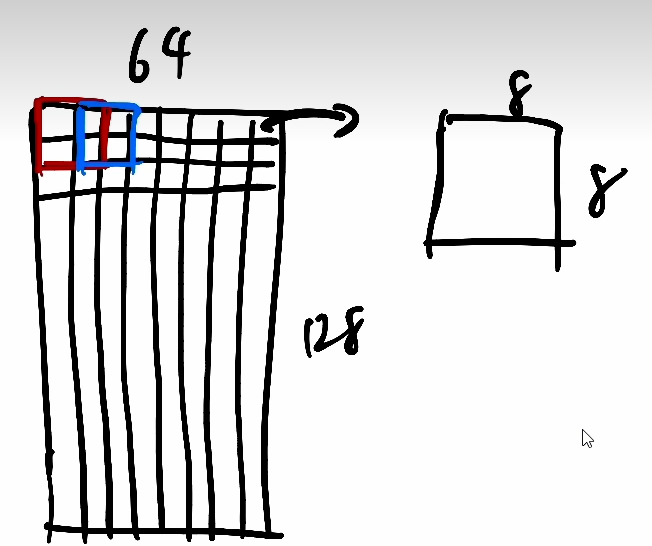
块滚动模式：步长为1个细胞（8 像素），如下图，从左上角开始先归一化红色块，然后计算下一个块：后移1个步长（即1个细胞/8 像素），找到蓝色块，这就是第二个块，以此类推，横向和纵向的步长是一样的。

为什么要块归一化？

假设光照增强，所有梯度模长翻倍，原始向量变为v = [2, 4, 6, 8, 10]：

L2 归一化后仍为 [0.135, 0.270, 0.405, 0.540, 0.674]
L1 归一化后仍为 [0.067, 0.133, 0.200, 0.267, 0.333]

可见，归一化后向量不受整体缩放影响，仅保留各元素的 “比例关系”，从而消除光照变化的干扰，让特征更鲁棒。

5、整合 HOG 特征向量

将所有块的归一化特征向量按顺序拼接，形成整幅图像的 HOG 特征。

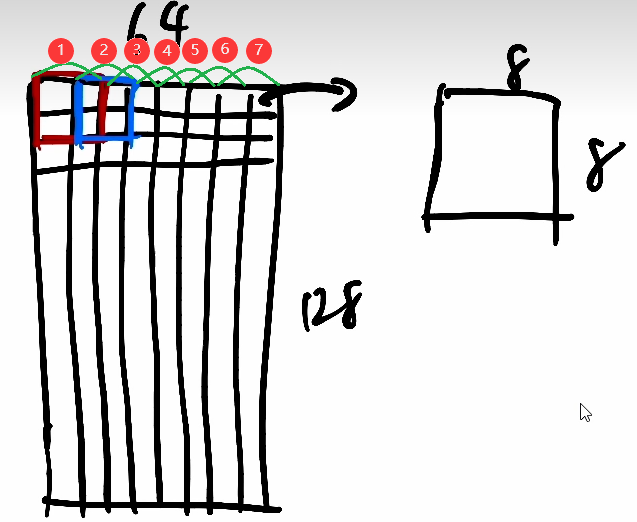
特征维度计算：假设图像大小为 128x64（行人检测常用尺寸），细胞 8x8，块 2x2 细胞（步长 8 像素），则：
- 水平方向块数：(64-16)/8 + 1 = 7（算一行多少块，因为每次挪一个细胞的步长，下图都可以直接数出来7个）
- 垂直方向块数：(128-16)/8 + 1 = 15
- 总块数：7x15=105，总特征维度：105x36=3780。

三.函数调用

创建 HOG 描述符：cv2.HOGDescriptor(参数)
- 用于创建 HOG 描述符对象，需要传入 HOG 的参数（窗口大小、块大小、块步长、细胞大小、方向直方图的区间数），定义特征提取的规则。
提取 HOG 特征：hog.compute(灰度图像)
- 这是实际计算 HOG 特征的函数，输入灰度图像，返回提取到的 HOG 特征向量（一维数组）。

import cv2

# 读取图像并转为灰度图
image = cv2.imread("test.jpg")
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 定义HOG参数
win_size = (64, 64)    # 检测窗口大小
block_size = (16, 16)  # 块大小（2x2细胞）
block_stride = (8, 8)  # 块步长（1个细胞）
cell_size = (8, 8)     # 细胞大小
nbins = 9              # 方向直方图的区间数

# 创建HOG描述符并计算特征
hog = cv2.HOGDescriptor(win_size, block_size, block_stride, cell_size, nbins)
hog_features = hog.compute(gray)  # 核心调用函数

print("HOG特征维度：", hog_features.shape)  # 输出特征维度