本文详细解析了B+树的Node节点存储结构，介绍了如何创建根节点、进行精准和范围搜索，以及插入新节点和处理节点分裂的过程。核心内容包括B+树的基本原理和关键操作实现。
代码地址：GitHub - zhangqingqing24630/MySQL-
此项目来源于何人听我楚狂声
目录
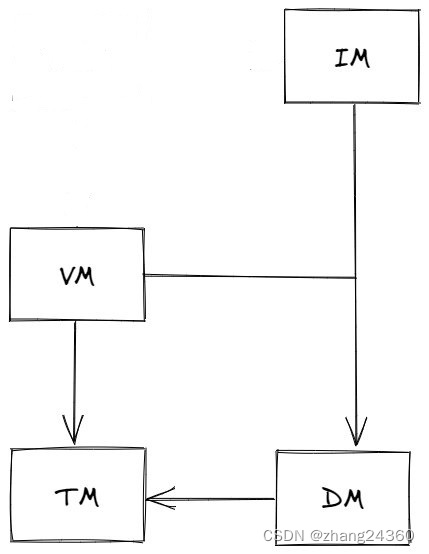
IM，即 Index Manager，索引管理器，为数据库提供了基于 B+ 树的聚簇索引
在依赖关系图中可以看到，IM 直接基于 DM，而没有基于 VM。要建立索引的数据同时被直接插入数据库文件中，而不需要经过版本管理。
Node节点
存储结构
二叉树由一个个 Node 组成，每个 Node 都存储在一条 DataItem 中的Data部分。结构如下：
Node结构如下：
二叉树由一个个 Node 组成，每个 Node 都存储在一条 DataItem 中
[LeafFlag][KeyNumber][SiblingUid]
占1个字节 2 8
[Son0][Key0][Son1][Key1]...[SonN][KeyN]
8 8 8
其中 LeafFlag 标记了该节点是否是个叶子节点；KeyNumber 为该节点中 key 的个数；
SiblingUid 是其兄弟节点存储在 DM 中的 UID。
后续是穿插的子节点（SonN）和 KeyN。
最后的一个 KeyN 始终为 MAX_VALUE其中 LeafFlag 标记了该节点是否是个叶子节点；
KeyNumber 为该节点中 key 的个数；
SiblingUid 是其兄弟节点存储在 DM 中的 UID。
后续是穿插的子节点SonN（索引的UID）和 KeyN（索引）。最后的一个 KeyN 始终为 MAX_VALUE，以此方便查找。
Node节点建立
Node 类持有了其 B+ 树结构的引用，DataItem 的引用和 SubArray 的引用，用于方便快速修改数据和释放数据。
每一个Node的大小是固定的，计算为NODE_SIZE。
BALANCE_NUMBER表示当一个Node所含子节点的个数=BALANCE_NUMBER*2时，会出现节点分裂。
public class Node {
static final int IS_LEAF_OFFSET = 0;
static final int NO_KEYS_OFFSET = IS_LEAF_OFFSET+1;
static final int SIBLING_OFFSET = NO_KEYS_OFFSET+2;
static final int NODE_HEADER_SIZE = SIBLING_OFFSET+8;
static final int BALANCE_NUMBER = 2;//32
//一个Node的大小
//一个key,Son都占8个字节
static final int NODE_SIZE = NODE_HEADER_SIZE + (2*8)*(BALANCE_NUMBER*2+2);
BPlusTree tree;
DataItem dataItem;
SubArray raw;
long uid;
...
}根节点建立
于是生成一个根节点的参数可以写成如下：
left 原来的根节点uid right，新的分裂出来的节点的uid Key新的分裂出来的节点的第一个索引
这种方法通常用于已有的根节点的基础上，建立新的根节点，把原来的根节点设置为新节点的第一个子节点
static byte[] newRootRaw(long left, long right, long key) {
//KeyNumber可以不同，但是每个Node的大小都相同
SubArray raw = new SubArray(new byte[NODE_SIZE], 0, NODE_SIZE);
//初始两个子节点为 left 和 right, 初始键值为 key。
setRawIsLeaf(raw, false);//该节点不是叶子节点
setRawNoKeys(raw, 2);//该节点有2个子节点
setRawSibling(raw, 0);//根节点无邻节点
//left||key || right||Long.MAX_VALUE
setRawKthSon(raw, left, 0);//left为第0个子节点的uid
setRawKthKey(raw, key, 0);//key值
setRawKthSon(raw, right, 1);
setRawKthKey(raw, Long.MAX_VALUE, 1);
}类似的，生成一个空的根节点数据，这种方法常用于建立B+树的第一个根节点时。
static byte[] newNilRootRaw() {
SubArray raw = new SubArray(new byte[NODE_SIZE], 0, NODE_SIZE);
setRawIsLeaf(raw, true);
setRawNoKeys(raw, 0);
setRawSibling(raw, 0);
return raw.raw;
}实现方法
精准搜索
searchNext 寻找对应 key 的 UID, 如果找不到, 则返回邻节点的 UID
定义一个搜索到的节点
class SearchNextRes {
long uid;//如果命中，返回命中节点的uid
long siblingUid;//如果没有命中，返回邻节点继续查询
}searchNext 在当前节点寻找对应 key 的 UID, 如果找不到, 则返回邻节点的 UID
//searchNext 在当前节点寻找对应 key 的 UID, 如果找不到, 则返回兄弟节点的 UID
public SearchNextRes searchNext(long key) {
dataItem.rLock();
try {
SearchNextRes res = new SearchNextRes();
int noKeys = getRawNoKeys(raw);//该节点有几个key
//System.out.println("no"+noKeys);
for(int i = 0; i < noKeys; i ++) {
//第i个节点的key
System.out.println("遍历到第几个子节点"+i);
long ik = getRawKthKey(raw, i);
System.out.println("该子节点的索引是ik="+ik);
if(key < ik) {//找到了
// 寻找对应 key 的 UID
res.uid = getRawKthSon(raw, i);
res.siblingUid = 0;
return res;
}
}
//如果找不到, 则返回兄弟节点的 UID
res.uid = 0;
res.siblingUid = getRawSibling(raw);
return res;
} finally {
dataItem.rUnLock();
}
}范围搜索
LeafSearchRange 方法在当前节点进行范围查找，范围是 [leftKey, rightKey]，这里约定如果 rightKey 大于等于该节点的最大的 key, 则还同时返回兄弟节点的 UID，方便继续搜索下一个节点。
class LeafSearchRangeRes {
List<Long> uids;//如果命中，返回范围内所有的uid
long siblingUid;//如果没有命中，返回下一个邻节点
}public LeafSearchRangeRes leafSearchRange(long leftKey, long rightKey) {
dataItem.rLock();
try {
int noKeys = getRawNoKeys(raw);//该节点有多少个子节点
int kth = 0;
while(kth < noKeys) {
//第k+1个子节点的key
long ik = getRawKthKey(raw, kth);
//找到了满足范围的第一个kth
if(ik >= leftKey) {
break;
}
kth ++;
}
List<Long> uids = new ArrayList<>();
while(kth < noKeys) {
long ik = getRawKthKey(raw, kth);
if(ik <= rightKey) {
uids.add(getRawKthSon(raw, kth));
kth ++;
//没有满足范围的索引
} else {
break;
}
}
long siblingUid = 0;
//该节点搜索完毕，则还同时返回兄弟节点的 UID，方便继续搜索下一个节点。
if(kth == noKeys) {
siblingUid = getRawSibling(raw);
}
LeafSearchRangeRes res = new LeafSearchRangeRes();
res.uids = uids;
res.siblingUid = siblingUid;
return res;
} finally {
dataItem.rUnLock();
}
}插入新的子节点
找到了待插入的位置，再插入uid|key，注意了，这里当待插入的位置是叶子节点和非叶子节点时，插法不同
1 如果要插入的是叶子节点，kth之后的节点右移，把key插入到kth位置
2 如果要插入的不是叶子节点，kth+1之后的节点右移，新插入节点的uid和原kth位置的key放到kth+1上，原kth位置的uid和待插入的key放到原kth位置
//找到了待插入的叶子节点Node，再插入uid|key
private boolean insert(long uid, long key) {
//该节点现有几个子节点
int noKeys = getRawNoKeys(raw);
int kth = 0;
System.out.println("no"+noKeys);
while(kth < noKeys) {
long ik = getRawKthKey(raw, kth);
System.out.println("ik="+ik);
if(ik < key) {
kth ++;
} else {
break;
}
}
//应该插入到raw的kth位置
//要插入节点要插在当前节点的最后位置，且当前节点已经有邻节点，返回插入失败，下一步在邻节点进行插入
if(kth == noKeys && getRawSibling(raw) != 0) return false;
//如果找到插入位置为kth，且该节点是叶子节点，在当前节点的kth位置插一个key|son
if(getRawIfLeaf(raw)) {
//从kth开始所有节点往右移动，新的节点插入到kth位置
shiftRawKth(raw, kth);
setRawKthKey(raw, key, kth);
setRawKthSon(raw, uid, kth);
setRawNoKeys(raw, noKeys+1);
} else {
System.out.println("插入操作不是叶子节点");
//思路如果找到插入位置为kth，但该节点不是叶子节点
//kth位置的索引移到kth+1上，kth位置放入新插入节点的索引
//kth+1位置的uid改成新插入节点的uid
//例如 把8插入到节点上
// [7 MAX_VALUE]
//[1 2] [5 7 9]
//变成
// [7 MAX_VALUE]此时，7存放的是[1 2]的uid，MAX_VALUE存放的是[5 7]的uid
//[1 2] [5 7] [8 9]
//private boolean insert(long uid, long key)这里uid是[8 9]的uid，key是8
//如果按照第一个if
//[7 8 MAX_VALUE]
//[1 2] [8 9] [5 7]
//如果按照else
//[7 8 MAX_VALUE]
//[1 2] [5 7] [8 9]
long kk = getRawKthKey(raw, kth);//kk=MAX_VALUE
System.out.println(key);
setRawKthKey(raw, key, kth);//key=8,kth=1
shiftRawKth(raw, kth+1);
setRawKthKey(raw, kk, kth+1);
setRawKthSon(raw, uid, kth+1);
setRawNoKeys(raw, noKeys+1);
}
return true;
}分裂Node节点
当节点的子节点装满时，需要分裂一个邻节点出来
private boolean needSplit() {
return BALANCE_NUMBER*2 == getRawNoKeys(raw);
}判断分裂方法 每当插入一个节点后，都会检查是否需要分裂节点。 1 如果插入不成功，把邻节点的uid赋值给siblingUid； 2 如果插入成功，但是需要分裂，把新分裂出来的节点的uid和索引赋值给newSon, newKey； 3 如果插入成功，不需要分裂，不做处理
class InsertAndSplitRes {
long siblingUid, newSon, newKey;
}分裂方法 1 在插入新的子节点后，节点已满的情况下，无法继续插入，此时，生成一个邻节点nodeRaw插入到原节点raw和原节点raw的邻节点之间， 2 把原节点raw后一半的数据拷贝到邻节点noderaw 3 此时，raw节点nodeRaw节点各有原来一半的数据，将nodeRaw节点设置为raw节点的邻节点 返回nodeRaw节点的uid和索引
private SplitRes split() throws Exception {
SubArray nodeRaw = new SubArray(new byte[NODE_SIZE], 0, NODE_SIZE);
setRawIsLeaf(nodeRaw, getRawIfLeaf(raw));
setRawNoKeys(nodeRaw, BALANCE_NUMBER);
setRawSibling(nodeRaw, getRawSibling(raw));
//从BALANCE_NUMBER（复制后一半的数据）开始把raw复制到noderaw里面，
copyRawFromKth(raw, nodeRaw, BALANCE_NUMBER);
//插入nodeRaw的uid
long son = tree.dm.insert(TransactionManagerImpl.SUPER_XID, nodeRaw.raw);
setRawNoKeys(raw, BALANCE_NUMBER);
setRawSibling(raw, son);
SplitRes res = new SplitRes();
//返回存储邻节点的uid和开头索引
res.newSon = son;
res.newKey = getRawKthKey(nodeRaw, 0);
//System.out.println(res.newKey);
return res;
}完整的插入并检查节点是否需要分裂的代码如下：
//如果分裂，返回分裂出的节点的信息
public InsertAndSplitRes insertAndSplit(long uid, long key) throws Exception {
boolean success = false;
Exception err = null;
InsertAndSplitRes res = new InsertAndSplitRes();
dataItem.before();
try {
success = insert(uid, key);
if(!success) {
//新插入的节点在当前节点的最后，且当前节点已经有邻节点
//插入不成功，返回邻节点
res.siblingUid = getRawSibling(raw);
return res;
}
//在插入新节点后raw节点已满的情况下，无法继续插入，
// 生成一个邻节点插入到raw和raw的邻节点之间，且邻节点会分担一半的数据
//返回存储邻节点的uid和开头索引
System.out.println("needSplit "+needSplit());
if(needSplit()) {
try {
SplitRes r = split();
res.newSon = r.newSon;
res.newKey = r.newKey;
return res;
} catch(Exception e) {
err = e;
throw e;
}
} else {
return res;
}
} finally {
if(err == null && success) {
dataItem.after(TransactionManagerImpl.SUPER_XID);
} else {
dataItem.unBefore();
}
}
}B+树
根节点
由于 B+ 树在插入删除时，会动态调整，根节点不是固定节点，于是设置一个 bootDataItem，该 DataItem 中存储了根节点的 UID。
public class BPlusTree {
DataItem bootDataItem;
//返回根节点的uid
private long rootUid() {
bootLock.lock();
try {
SubArray sa = bootDataItem.data();
return Parser.parseLong(Arrays.copyOfRange(sa.raw, sa.start, sa.start+8));
} finally {
bootLock.unlock();
}
}
}动态调整根节点如下，可以注意到，IM 在操作 DM 时，使用的事务都是 SUPER_XID，表示永远处于可提交状态
//left 原来的根节点uid
// right，新的分裂出来的节点的uid
// rightKey新的分裂出来的节点的第一个索引
private void updateRootUid(long left, long right, long rightKey) throws Exception {
//System.out.println("key"+rightKey);
bootLock.lock();
try {
//生成一个根节点
byte[] rootRaw = Node.newRootRaw(left, right, rightKey);
//返回要插入的根节点的uid
long newRootUid = dm.insert(TransactionManagerImpl.SUPER_XID, rootRaw);
bootDataItem.before();
SubArray diRaw = bootDataItem.data();
//替换uid为新的uid
System.arraycopy(Parser.long2Byte(newRootUid), 0, diRaw.raw, diRaw.start, 8);
bootDataItem.after(TransactionManagerImpl.SUPER_XID);
} finally {
bootLock.unlock();
}
}节点插入
同理，在一个完整的B+树节点插入时，需要从根节点搜索，直到寻找需要插入的叶子节点位置进行插入。如果根节点已满，需要生成一个新的根节点，动态调整根节点信息
//从根节点开始查找，插入一个新节点
public void insert(long key, long uid) throws Exception {
long rootUid = rootUid();
//从rootUid节点（一直在变,但永远是bootItem里的值）开始找到要插入的叶子节点位置插入
InsertRes res = insert(rootUid, uid, key);
assert res != null;
//原节点已满，分裂出一个新的节点，则生成一个根节点，根节点的key保存原节点和新节点的key|uid。
if(res.newNode != 0) {
System.out.println("根节点已满，需要生成一个新的根节点");
updateRootUid(rootUid, res.newNode, res.newKey);
}
}//从nodeUid节点开始找到要插入的位置插入
//如果nodeUid是叶子节点，直接插入
//如果nodeUid不是叶子节点，在下一层找到叶子节点再插入
private InsertRes insert(long nodeUid, long uid, long key) throws Exception {
//从哪个节点开始遍历插入的位置
Node node = Node.loadNode(this, nodeUid);
boolean isLeaf = node.isLeaf();
node.release();
InsertRes res = null;
System.out.println("找到的节点是不是叶子节点"+isLeaf);
//如果nodeUid是叶子节点
if(isLeaf) {
//往nodeUid大节点处存key|uid信息
//如果分裂，返回分裂出的节点的信息
res = insertAndSplit(nodeUid, uid, key);
} else {
//（同层查找）在当前节点查找，找不到就返回邻节点查找，返回找到的key的uid或者邻节点的uid
long next = searchNext(nodeUid, key);
//如果不是叶子节点，继续在下一层搜索直到找到对应的叶子节点位置，当叶子节点满时，返回新分裂出的节点位置。
InsertRes ir = insert(next, uid, key);
//把分裂节点插入到一个非叶子节点上
if(ir.newNode != 0) {
//若分裂出节点，把分裂节点的key|uid添加到对应的父节点中。
//如果原来的父节点已满，就会重新分裂出一个父节点，会返回分裂出的父节点。
res = insertAndSplit(nodeUid, ir.newNode, ir.newKey);
} else {
res = new InsertRes();
}
}
return res;
}范围查询
与Node节点类似，不过要先一直定位到对应的叶子节点的位置，再按照Node节点的查询方法进行查询
public List<Long> searchRange(long leftKey, long rightKey) throws Exception {
long rootUid = rootUid();
//从uid为rootUid的节点开始寻找索引为leftKey的数据的叶子节点的uid
long leafUid = searchLeaf(rootUid, leftKey);
List<Long> uids = new ArrayList<>();
while(true) {
Node leaf = Node.loadNode(this, leafUid);
LeafSearchRangeRes res = leaf.leafSearchRange(leftKey, rightKey);
leaf.release();
uids.addAll(res.uids);
if(res.siblingUid == 0) {
break;
} else {
leafUid = res.siblingUid;
}
}
return uids;
}//从uid为nodeUid的节点开始寻找索引为key的数据的uid(直到找到叶子节点)
private long searchLeaf(long nodeUid, long key) throws Exception {
Node node = Node.loadNode(this, nodeUid);
boolean isLeaf = node.isLeaf();
node.release();
if(isLeaf) {
//叶子节点
return nodeUid;
} else {
//找到索引为key的uid，继续往下搜索，直到搜到叶子节点
long next = searchNext(nodeUid, key);
return searchLeaf(next, key);
}
}IM 不用提供删除索引的能力。当上层模块通过 VM 删除某个 Entry，实际的操作是设置其 XMAX。如果不去删除对应索引的话，当后续再次尝试读取该 Entry 时，是可以通过索引寻找到的，但是由于设置了 XMAX，寻找不到合适的版本而返回一个找不到内容的错误。
测试代码
public class test {
public static void main(String[] args) throws Exception {
TransactionManagerImpl tm=TransactionManager.create("cun/tm");
DataManager dm=DataManager.create("cun/dm",1 << 20,tm);
//1 生成一个空的根节点，存入到一个dataItem中，会返回一个存放dataItem的rootuid
//再把rootuid存入，返回存放rootuid的uid
long uid=BPlusTree.create(dm);
System.out.println("存放rootuid的是"+uid);
//2 以该空节点为根节点建立B+树
//通过uid找到根节点的rootuid（在变），从而定位到根节点
BPlusTree bt=BPlusTree.load(uid,dm);
for(int i=1;i<=4;i++){
System.out.println(i);
bt.insert(2*i,i*2);
}
//当一个Node的子节点满时，生成一个新的邻节点，并重新设置根节点
//此时的根节点就不是叶子节点了
for(int i=5;i<=6;i++){
System.out.println(i);
bt.insert(2*i,i*3);
}
System.out.println(bt.searchRange(10,12));
}
}其B+树建立大致如下
[2 4 6 8]
变为
[6 MAX_VALUE]
[2 4] [6 8]
变为
[6 MAX_VALUE]
[2 4] [6 8 10 12]
变为
[6 MAX_VALUE]
[2 4] [6 8] [10 12]
变为
[6 10 MAX_VALUE]
[2 4] [6 8] [10 12]
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
