word2vec理解及pytorch实现

word2vec是Google研究团队的成果之一，它作为一种主流的获取分布式词向量的工具，在自然语言处理、数据挖掘等领域有着广泛的应用。本文首先会介绍一些预备知识，比如softmax、ngram、subsampling、neg-sampling等，之后来讲解word2vec的原理，并着手使用pytorch搭建word2vec模型。

word2vec优点

word2vec词向量与传统的one-hot词向量相比，主要有以下两个优势

1.低维稠密

一般来说分布式词向量的维度设置成100-500就足够使用，而one-hot类型的词向量维度与词表的大小成正比，是一种高维稀疏的表示方法，这种表示方法导致其在计算上效率比较低。

2.蕴含语义信息

one-hot这种表示方式使得每一个词映射到高维空间中都是互相正交的，也就是说one-hot向量空间中词与词之间没有任何关联关系，这显然与实际情况不符合，因为实际中词与词之间有近义、反义等多种关系。Word2vec虽然学习不到反义这种高层次语义信息，但它巧妙的运用了一种思想：“具有相同上下文的词语包含相似的语义”，使得语义相近的词在映射到欧式空间后中具有较高的余弦相似度。
$$sim(apple,banana)=\frac{ve{c}_{apple}\cdot ve{c}_{banana}}{|ve{c}_{apple}|\cdot |ve{c}_{banana}|}$$

图1

Skip-gram模型

1.训练样本

怎么把“具有相同上下文的词语包含相似的语义”这种思想融入模型是很关键的一步，在模型中，两个词是否出现在一起是通过判断这两个词在上下文中是否出现在一个窗口内。例如，原始样本“The quick brown fox jumps over the lazy dog.”在送入模型前会经过图2所示处理（这里为了绘图简单假设窗口为2，一般窗口是设置成5）。

如图所示，skip-gram模型的输入是当前词，输出是当前词的上下文，虽然我们训练模型的时候喂的是一个个分词好的句子，但内部其实是使用一个个word pair来训练。同样是之前的case“The quick brown fox jumps over the lazy dog.”，假如窗口改为5，则（The，quick）这个word pair会成为一个训练样本。

假如两个词具有相同的输出，则可反推出作为输入的两个词之间具有较高相似性，接下来就是如何使用模型来实现上述目标。

图2

2.skip-gram

skip-gram模型与自编码器（Autoencoder）类似，唯一的区别在于自编码器的输出等于输入，而skip-gram模型的输出是输入的上下文。那么，作为训练样本的word pair应该以什么样的方式输入给模型？ 答案是one-hot向量，为了得到one-hot向量，必须首先知道训练语料中包含了多少词。因此，在训练之前会首先对语料进行统计，得到词表。假设词表长度为10000，词向量为300维，则skip-gram模型可表示为图3。

图3

如图3所示，假设输入的word pair为（ants, able），则模型拟合的目标是$MaxP(able|ants)$，同时也需要满足$MinP(otherwords|ants)$，这里利用的是对数似然函数作为目标函数。上述表述中可表示为$P(able|ants)$：
$$P(able|ants)=softmax(X_{ants1\times 10000}\cdot W_{10000\times 300})$$
$$softmax(X)=\frac{exp(X_{1\times 300}\cdot W_{300\times 1})}{{\sum }_{i=1}^{10000}exp(X_{1\times 300}^i\cdot W_{300\times 1})}$$
根据$P(able|ants)$和$P(otherwords|ants)$，可构建似然函数：
$$L(W)=P(able|ants{)}^{y=able}\cdot P(otherwords|ants{)}^{y=otherwords}$$
则：
l o g   L ( W ) = { y = t a r g e t   w o r d } { l o g   P ( a b l e ∣ a n t s ) + l o g   P ( o t h e r   w o r d s ∣ a n t s ) } = ∑ i 10000 { y = t a r g e t   w o r d } l o g P ( w o r d i ∣ a n t s ) log \ L(W) = \{y=target \ word \} \{log \ P(able|ants) + log \ P(other \ words |ants) \} \\ = \sum_{i}^{10000} \{ y=target \ word \}logP(word_i|ants) log L(W)={y=target word}{log P(able∣ants)+log P(other words∣ants)}=i∑10000​{y=target word}logP(wordi​∣ants)
将$P(wor{d}_i|ants)$代入有：
l o g L ( W ) = ∑ i 10000 { y = t a r g e t   w o r d } l o g e x p ( X 1 × 300 ⋅ W 300 × 1 ) ∑ i = 1 10000 e x p ( X 1 × 300 i ⋅ W 300 × 1 ) logL(W)=\sum_i^{10000}\{ y=target \ word\}log \frac {exp(X_{1 \times 300}·W_{300 \times 1})} {\sum_{i=1}^{10000}exp(X_{1 \times 300}^i·W_{300 \times 1})} logL(W)=i∑10000​{y=target word}log∑i=110000​exp(X1×300i​⋅W300×1​)exp(X1×300​⋅W300×1​)​

式中{*}表示如果表达式*为true，则{*}=1，否则{*}=0。接下来要做的是最大化似然函数，也即：
$$MaxlogL(W)$$
要实现上述目标，可利用梯度上升法，首先对参数求偏导：
∂ l o g L ( W ) ∂ w i = x i ( { y = t a r g e t   w o r d } − P ( t a r g e t   w o r d ∣ x i ; W ) ) \frac{\partial logL(W)}{\partial w_i}=x_i(\{ y=target \ word \} - P(target \ word|x_i;W)) ∂wi​∂logL(W)​=xi​({y=target word}−P(target word∣xi​;W))
接下来根据学习率对进行更新：
$$w_i=w_i+\eta \cdot \frac{\partial logL(W)}{\partial w_i}$$
隐藏层的参数矩阵$W_{10000\times 300}$就包含了所有词的词向量，该矩阵的行为词表长度，列为词向量维度，矩阵中的每一行表示一个词的词向量。由于输入层$X_{ants1\times 10000}$是one-hot向量，与隐藏层$W_{10000\times 300}$点乘后其实是选中了该矩阵中的一行，如图5所示，这一行表示的是ants的词向量，而输出层其实是以ants的词向量为特征，以ants的上下文词作为类别来训练softmax分类器。

负采样 negative sample

以图3所示的模型为例，对每一个训练样本需要更新的参数个数有三百万（准确的说是三百万零三百，由于输入是one-hot，隐藏层每次只需要更新输入词语的词向量），这还是假设词表只有一万的情况下，实际情况会有五十万甚至更多，这时候参数就达到了亿级。训练过程中要对每个参数计算偏导，然后进行更新，这需要很大的计算资源。

负采样是加快训练速度的一种方法，这里的负可以理解为负样本。针对训练样本（ants, able），able这个词是正样本，词表中除able外的所有词都是负样本。负采样是对负样本进行采样，不进行负采样时，对每一个训练样本模型需要拟合一个正样本和九千九百九十九个负样本。加入负采样后，只需要从这九千九百九十九个负样本中挑出来几个进行拟合，大大节省了计算资源。那么应该挑几个负样本，根据什么进行挑呢？Google给出的建议是挑5-20个，怎么挑是根据词在语料中出现的概率，概率越大越有可能被选中，具体计算公式为：
$$P(word)=\frac{f(word{)}^{\frac{3}{4}}}{{\sum }_{i=1}^{10000}(f(wor{d}_i{)}^{\frac{3}{4}})}$$
其中f(word)表示word出现的概率。

那么如何使用负采样数据呢？下面会对使用负采样后的优化目标进行推导。
考虑一对单词和上下文的组合$(w,c)$。我们用$p(D=1|w,c)$表示$(w,c)$是真实上下文对的概率。相应地，$p(D=0|w,c)=1-p(D=1|w,c)$将是$(w,c)$不是真实上下文对的概率。假设存在控制分布的参数$\theta ：p(D=1|w,c;\theta )$。

根据论文，我们假设单词和上下文来自不同的词汇表，因此，单词dog相关联的向量将与上下文dog相关联的向量不同。做出这种假设的一个可能的解释如下：考虑单词dog和上下文dog共享相同向量$v$的情况。单词几乎不会出现在自身的上下文中，因此模型应该为$p(dog|dog)$分配一个低概率，这需要为$v\cdot v$分配一个低值，这是不可取的。
我们现在的目标是找到参数，以最大化所有单词上下文对确实是真实的概率，即：
$$\begin{gathered} arg\underset{\theta }{\max }\prod _{(w,c)\in D}p(D=1|w,c;\theta ) \\ =arg\underset{\theta }{\max }log\prod _{(w,c)\in D}p(D=1|w,c;\theta ) \\ =arg\underset{\theta }{\max }\sum _{(w,c)\in D}logp(D=1|w,c;\theta ) \end{gathered}$$
$p(D=1|w,c;\theta )$可以用softmax定义：
$$p(D=1|w,c;\theta )=\frac{1}{1+e^{-v_c\cdot v_w}}$$
优化目标是：
$$arg\underset{\theta }{\max }\sum _{(w,c)\in D}\frac{1}{1+e^{-v_c\cdot v_w}}$$
我们需要一种机制，通过禁用某些$(w,c)$组合来阻止所有向量具有相同的值。负采样就满足这种情况，负样本对不是真实数据，因此其$p(D=1|w,c;\theta )$是很低的，设负样本集合为D’，优化目标为：
$$\begin{gathered} arg\underset{\theta }{\max }\prod _{(w,c)\in D}p(D=1|w,c;\theta )\prod _{(w,c)\in D^{\prime }}p(D=0|w,c;\theta ) \\ =arg\underset{\theta }{\max }log\prod _{(w,c)\in D}p(D=1|w,c;\theta )\prod _{(w,c)\in D^{\prime }}(1-p(D=1|w,c;\theta )) \\ =arg\underset{\theta }{\max }\sum _{(w,c)\in D}logp(D=1|w,c;\theta )+\sum _{(w,c)\in D^{\prime }}log(1-p(D=1|w,c;\theta )) \\ =arg\underset{\theta }{\max }\sum _{(w,c)\in D}log\frac{1}{1+e^{-v_c\cdot v_w}}+\sum _{(w,c)\in D^{\prime }}log(1-\frac{1}{1+e^{-v_c\cdot v_w}}) \\ =arg\underset{\theta }{\max }\sum _{(w,c)\in D}log\frac{1}{1+e^{-v_c\cdot v_w}}+\sum _{(w,c)\in D^{\prime }}log\frac{1}{1+e^{v_c\cdot v_w}} \end{gathered}$$

令$\sigma =\frac{1}{1+e^{-x}}$，可得：

$$\begin{gathered} arg\underset{\theta }{\max }\sum _{(w,c)\in D}log\frac{1}{1+e^{-v_c\cdot v_w}}+\sum _{(w,c)\in D^{\prime }}log\frac{1}{1+e^{v_c\cdot v_w}} \\ =arg\underset{\theta }{\max }\sum _{(w,c)\in D}log\sigma (v_c\cdot v_w)+\sum _{(w,c)\in D^{\prime }}log\sigma (-v_c\cdot v_w) \end{gathered}$$
我们可看到这个就是原文中的优化目标。

欠采样 subsample

图2中的例子中“the”这种词在任何场景中都可能出现，它们并不包含多少语义，而且出现的频率特别高，如果不加处理会影响词向量的效果。欠采样就是为了应对这种现象，它的主要思想是对每个词都计算一个采样概率，根据概率值来判断一个词是否应该保留。概率计算方法为：
$$P(word)=\left(\sqrt{\frac{f(word)}{0.001}}+1\right)\cdot \frac{0.001}{f(word)}$$
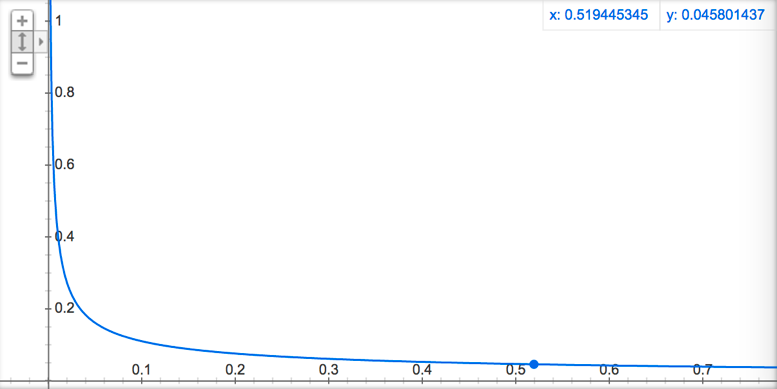
其中f(*)表示*出现的概率，0.001为默认值，具体函数走势如图4所示，可以看出，词语出现的概率越高，其被采样到的概率就越低。这里有一点IDF的味道，不同的是IDF是为了降低词的特征权重，欠采样是为了降低词的采样概率。

图4

pytorch实现

待续