常见排序算法简介

最新推荐文章于 2025-09-22 20:39:32 发布

原创最新推荐文章于 2025-09-22 20:39:32 发布 · 707 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#排序 #快速排序 #希尔排序 #堆排序

数据结构和算法专栏收录该内容

4 篇文章

订阅专栏

选择排序
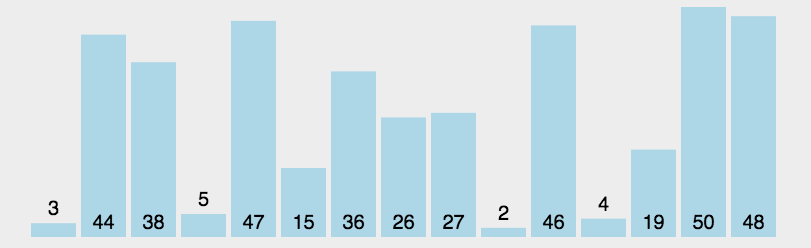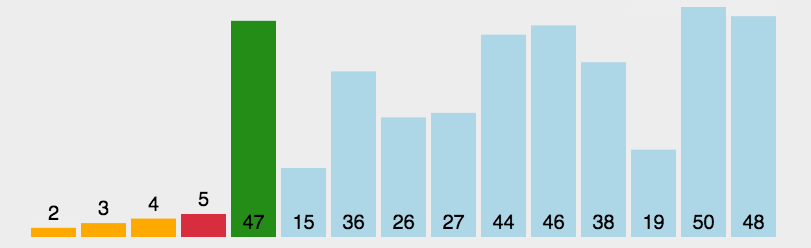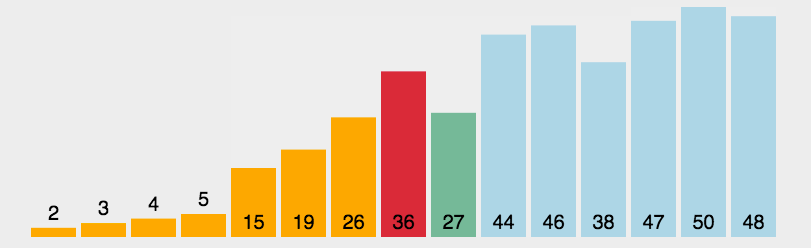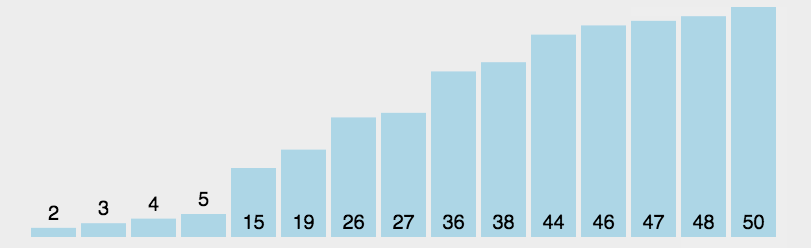
每次从待排序的序列中选出一个最小的数，放到已排好序的序列末尾

func SelectionSort(s []int) []int {
	for i := 0; i < len(s) - 1; i++ {
		minPos := i
		for j := i+1; j < len(s); j++ {
			if s[minPos] > s[j] {
				minPos = j
			}
		}
		if minPos != i {
			s[i], s[minPos] = s[minPos], s[i]
		}
	}
	return s
}

时间复杂度：O(n^2)

冒泡排序
对待排序的序列相邻的两个数依次两两比较，把较大的数放到后面，每一轮下来最大的数就会跑到序列最末端，再对剩下的数继续这样操作，较大的数往下沉，较小的数往上浮

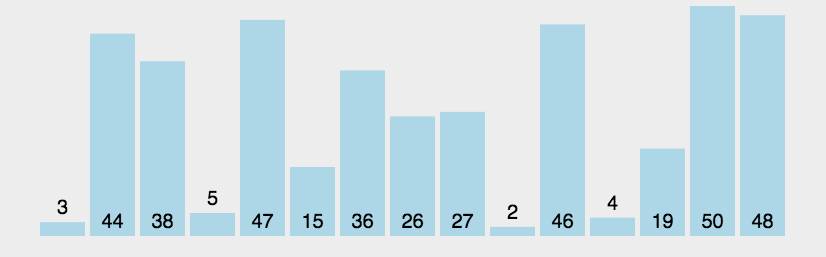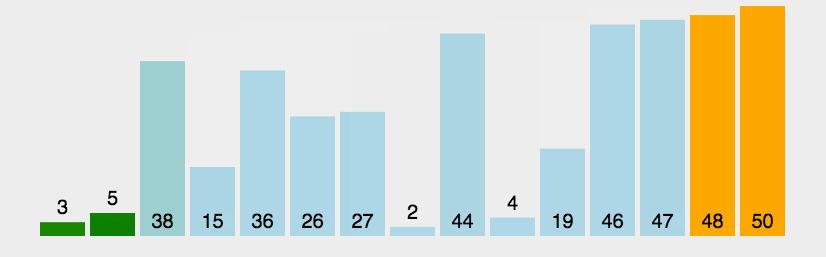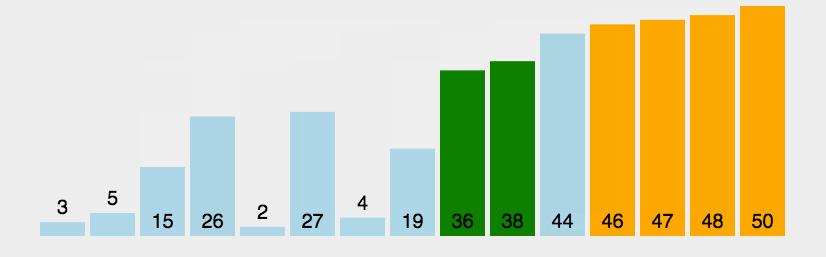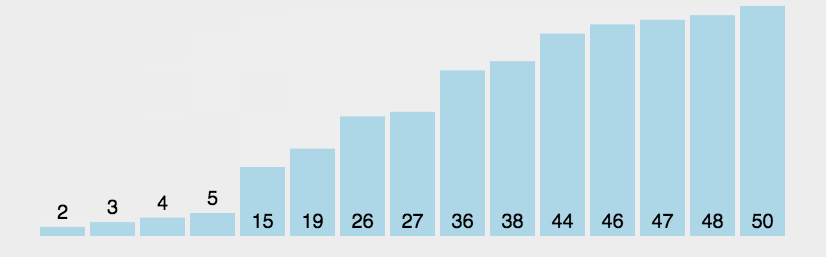
func BubbleSort(s []int) []int {
	for i := 0; i < len(s) - 1; i++ {
		for j := 0; j < len(s) - 1 - i; j++ {
			if s[j] > s[j+1] {
				s[j], s[j+1] = s[j+1], s[j]
			}
		}
	}
	return s
}

时间复杂度：O(n^2)

插入排序
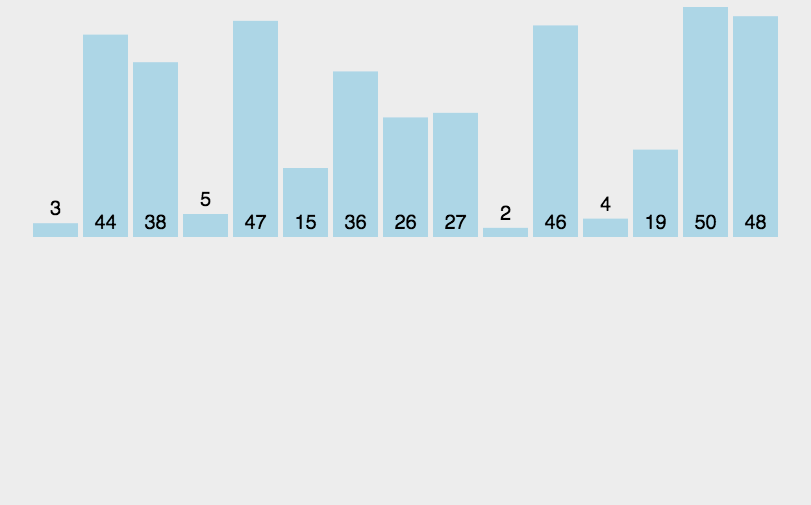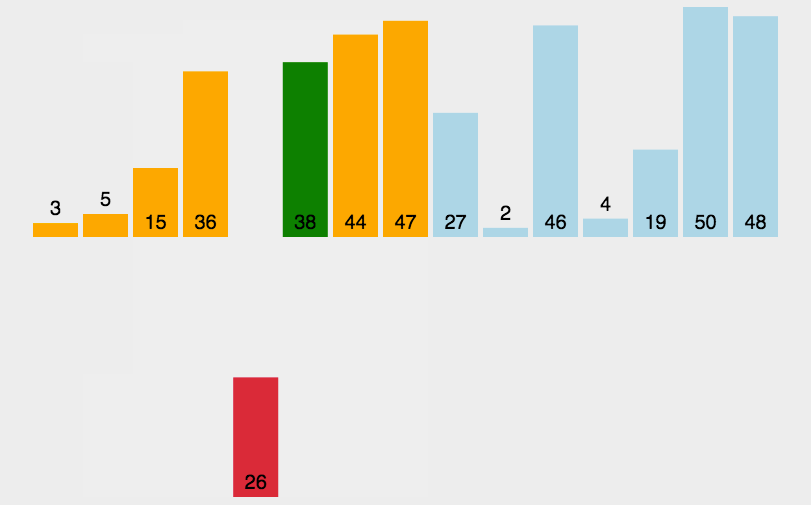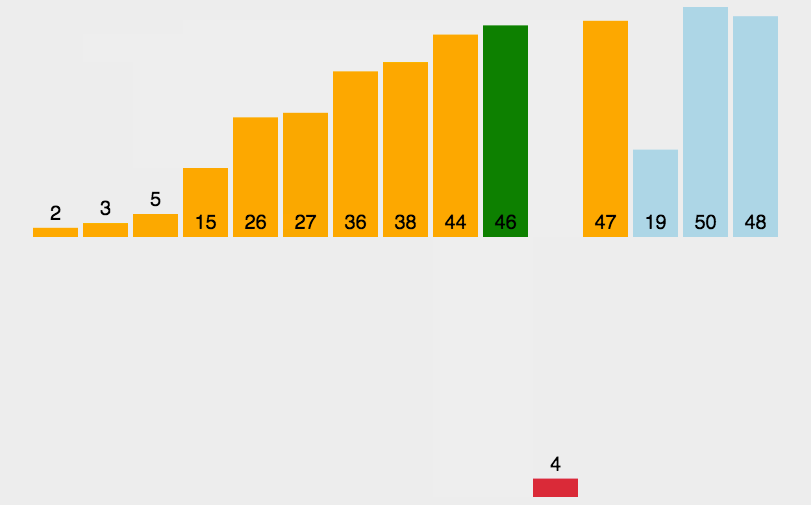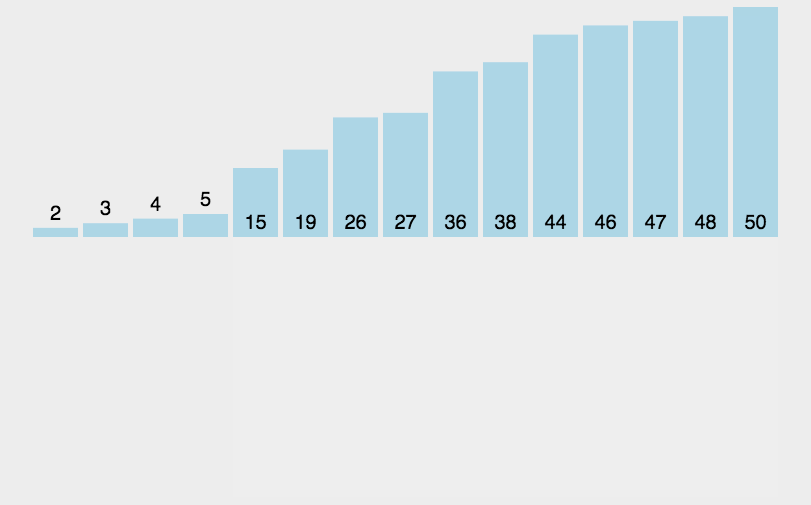
从未排好序的序列中依次选择一个数，在已排好序的序列中找到这个数应该所在的位置，然后插入该位置。

func InsertSort(s []int) []int {
	for i := 1; i < len(s); i++ {
		for j := i; j > 0; j-- {
			if s[j] < s[j-1] {
				s[j], s[j-1] = s[j-1], s[j]
			} else {
				break
			}
		}
	}
	return s
}

可以进一步精简代码

func InsertSort(s []int) []int {
	for i := 1; i < len(s); i++ {
		for j := i; j > 0 && s[j] < s[j-1]; j-- {
			s[j], s[j-1] = s[j-1], s[j]
		}
	}
	return s
}

时间复杂度：O(n^2)

希尔排序
第一种突破 O(n^2) 时间复杂度的排序，一种经过优化的插入排序，它是基于这样一种原理：一个序列越有序，则插入排序的性能越高，比如对于一个原本就是有序的序列，插入排序的时间复杂度能达到O(n)，希尔排序按下标的跨度将数组分成若干小组，对每个小组分别使用插入排序，然后减小跨度重复上述操作，当跨度减为1时就只有一个包含全部数的分组，再使用插入排序完成排序。
比如一组数是: 8, 9, 1, 7, 2, 3, 5, 4, 6, 0

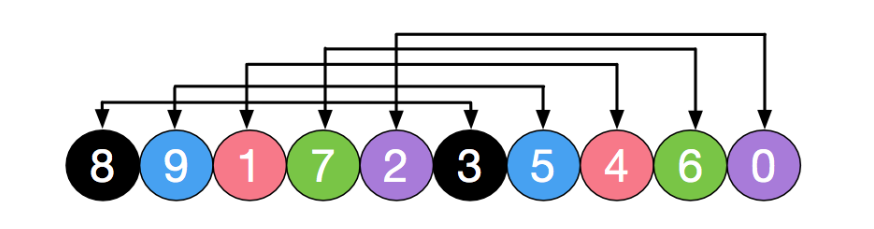
第一次使用数组长度的一半5作为下标步长进行分组，分成了 [8, 3], [9, 5], [1, 4], [7, 6], [2, 0]，对这五组数分别使用插入排序进行排序

第二次使用 5 / 2 = 2 作为步长再进行分组，分成两组分别进行插入排序

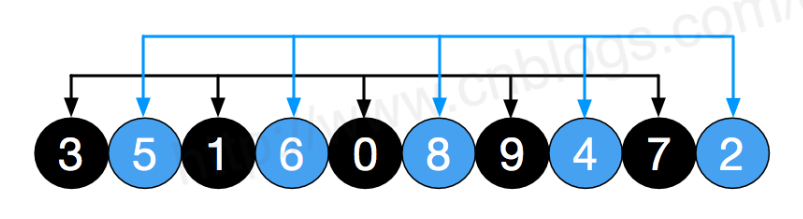
排好序后如下

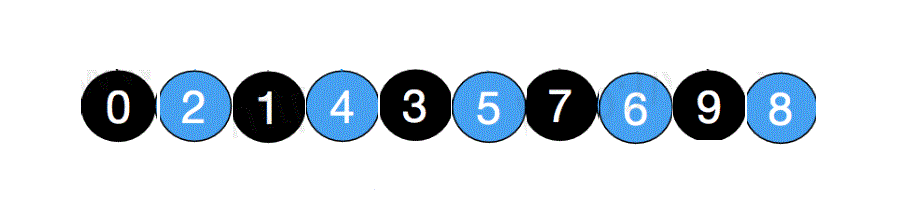
第三步使用步长为1进行分组，其实就是全部数作为一组，再进行插入排序，然后排序就完成了。

func ShellSort(s []int) []int {
	for step := len(s) / 2; step > 0; step /= 2 {
		for i := 0; i < step; i++ {
			for j := i + step; j < len(s); j += step {
				for k := j; k >= step && s[k] < s[k-step]; k -= step {
					s[k], s[k-step] = s[k-step], s[k]
				}
			}
		}
	}
	return s
}

对每个分组进行排序，可以一组一组的排，排完第一组再排第二组，也可以先排所有分组的前两个数，然后再排所有分组的第三个数，第四个数。。。因此可以优化为：

func ShellSort(s []int) []int {
	for step := len(s) / 2; step > 0; step /= 2 {
		for j := step; j < len(s); j ++ {
			for k := j; k >= step && s[k] < s[k-step]; k -= step {
				s[k], s[k-step] = s[k-step], s[k]
			}
		}
	}
	return s
}

时间复杂度：O(n^1.3) ~ O(n^2)
希尔排序和插入排序实测性能对比

func InsertSort(s []int) []int {
	cnt := 0
	for i := 1; i < len(s); i++ {
		for j := i; j > 0 && s[j] < s[j-1]; j-- {
			s[j], s[j-1] = s[j-1], s[j]
			cnt ++
		}
	}
	fmt.Println("InsertSort 循环次数：", cnt)
	return s
}

func ShellSort(s []int) []int {
	cnt := 0
	for step := len(s) / 2; step > 0; step /= 2 {
		for j := step; j < len(s); j ++ {
			for k := j; k >= step && s[k] < s[k-step]; k -= step {
				s[k], s[k-step] = s[k-step], s[k]
				cnt ++
			}
		}
	}
	fmt.Println("ShellSort 循环次数：", cnt)
	return s
}

func main() {
	rand.Seed(time.Now().UnixNano())
	s1, s2 := make([]int, 10000), make([]int, 10000)
	for i := 0; i< 10000; i++ {
		r := rand.Intn(900000)
		s1[i], s2[i] = r, r
	}
	InsertSort(s1)
	ShellSort(s2)
}

InsertSort 循环次数： 25147593
ShellSort 循环次数： 154287

快速排序
在实际应用中广泛使用的排序算法，比如PHP中的sort类函数基本使用快排

Golang中的排序结合了多种排序方法，当然快排是必不可少的

这种排序方式主要原理是从数组中随机选一个数（称做pivot），比如第一个数，然后把数组中比他小的数移动到它的左边，比它大的数移动到它的右边，然后对左右两边的数再重复进行这样的操作，直到整个数组排好序。

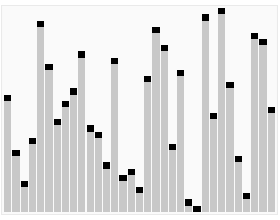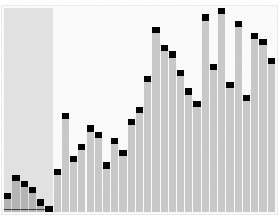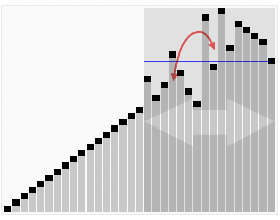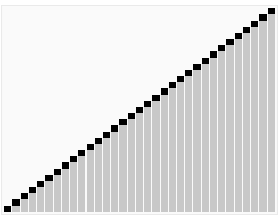
在这里插入图片描述
关键的问题是怎么把数组中比它小的数移到它的左边，比它大的数移到它的右边。
一种简单朴素的想法，遇到比pivot小的数，把pivot到当前这个较小的数之间的数整体往后移动一位，最后把这个较小的数放到pivot之前这个空位上。

func Partition(s []int) int {
	if len(s) == 0 {
		return 0
	}
	pivotPos := 0
	for i := 1; i < len(s); i++ {
		if s[i] < s[pivotPos] {
			tmp := s[i]
			copy(s[pivotPos+1:i+1], s[pivotPos:i])
			s[pivotPos] = tmp
			pivotPos++
		}
	}
	return pivotPos
}

func main() {
	s := []int{20, 34, 1, 16, -3, 133, 16, 59, 21, 4}
	fmt.Println(Partition(s), s)
}

5 [1 16 -3 16 4 20 34 133 59 21]

实现没问题，但是需要大量移动元素，性能显然不好，大佬们想出了更好的方式

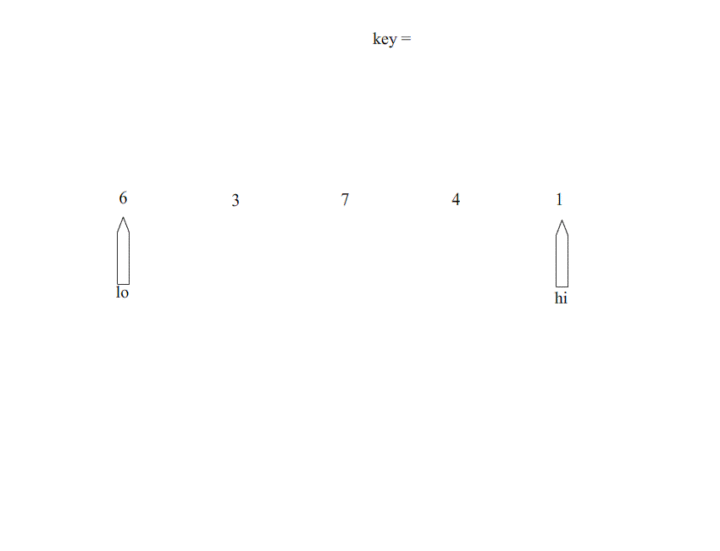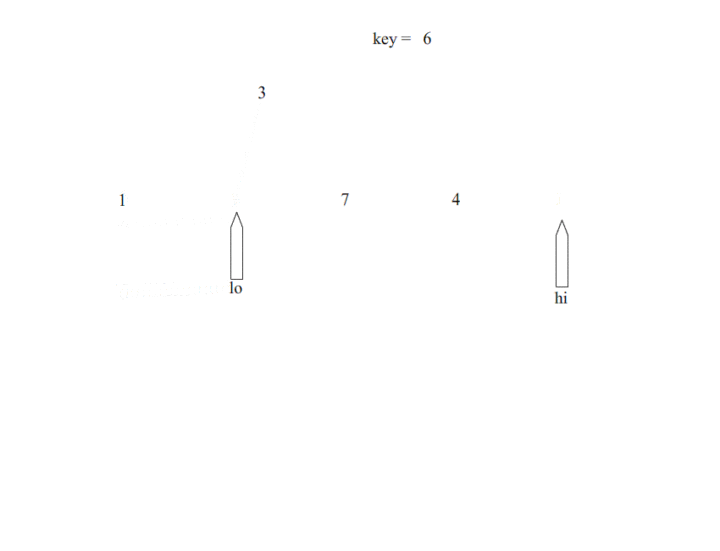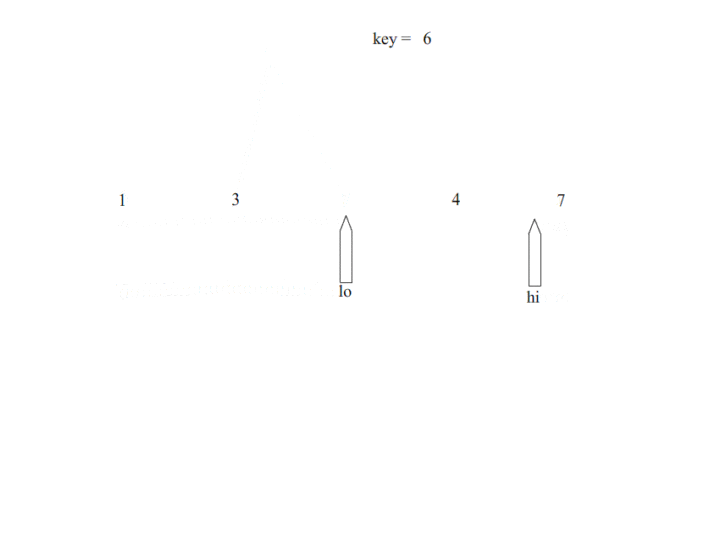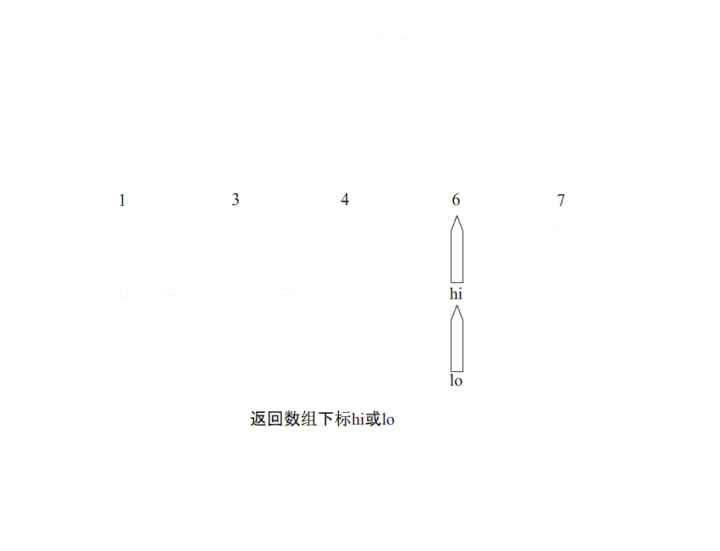
在这里插入图片描述
在数组的起始位置和结束位置分别放置一个指针，遇到一个比pivot小的数，左指针位置+1，遇到一个比pivot大的数，右指针位置-1，当左右指针重合的时候，就是pivot应该所在的位置。

func Partition(s []int) int {
	if len(s) <= 1 {
		return len(s) - 1
	}
	low, high := 0, len(s) - 1
	pivot, slot := s[0], 0
	for low < high {
		if low == slot {
			if s[high] >= pivot {
				high --
			} else {
				s[slot] = s[high]
				low ++
				slot = high
			}
		} else {
			if s[low] <= pivot {
				low ++
			} else {
				s[slot] = s[low]
				high --
				slot = low
			}
		}
	}
	s[low] = pivot
	return low
}

另外一种方式，遍历数组，每找到一个比pivot小的数，pivot的位置pos就应该向后移一位，同时要保证pos之前的数都小于pivot，最后把pos这个位置上的值置为 pivot即可

func Partition(s []int) {
	pivot, ShouldPos, hole := s[0], 0, 0
	for i := 1; i < len(s); i++ {
		if s[i] < pivot {
			s[i], s[ShouldPos] = s[ShouldPos], s[i]
			if ShouldPos == hole {
				hole = i
			}
			ShouldPos++
		}
	}
	s[hole], s[ShouldPos] = s[ShouldPos], pivot
}

这个还可以优化

func Partition(s []int) {
	ShouldPos := 0
	for i := 1; i < len(s); i++ {
		if s[i] < s[0] {
			ShouldPos++
			if i != ShouldPos {
				s[i], s[ShouldPos] = s[ShouldPos], s[i]
			}
		}
	}
	s[0], s[ShouldPos] = s[ShouldPos], s[0]
}

上面任何一个方法加个递归就是快排的实现

func Partition(s []int) {
	ShouldPos := 0
	for i := 1; i < len(s); i++ {
		if s[i] < s[0] {
			ShouldPos++
			if i != ShouldPos {
				s[i], s[ShouldPos] = s[ShouldPos], s[i]
			}
		}
	}
	s[0], s[ShouldPos] = s[ShouldPos], s[0]

    // 对pivot左右部分的子数组递归上述操作
	if ShouldPos > 0 {
		Partition(s[:ShouldPos])
	}
	if ShouldPos < len(s) - 1 {
		Partition(s[ShouldPos+1:])
	}
}

平均时间复杂度：O(n log n)，最坏时间复杂度：O(n^2)
由于pivot的选取影响到快排的性能，一种优化的pivot选取的方式是
s[low], s[(low + high) / 2], s[high] 三者中选中间的那个值作为pivot。

归并排序
把数组从中间一分为二，然后对一分为二的两个子数组继续一分为二，一直分直到不能再分为止，即一个子数组中只有一个元素，这时再反向的归并有序子数组，最终得到排好序的数组。

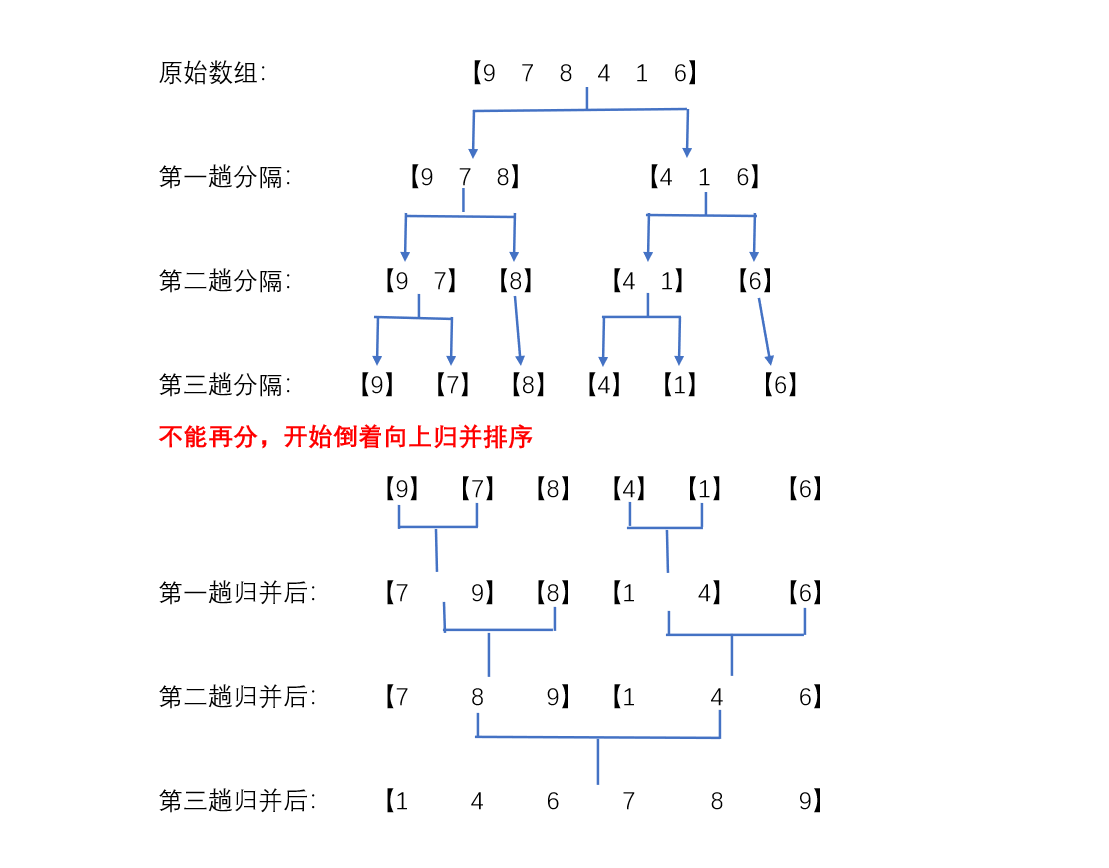
归并排序有两个点，一是切割，二是归并有序子数组
归并两个有序数组

func Merge(s1, s2 []int) []int{
	merged := make([]int, len(s1) + len(s2))
	i, j, idx := 0, 0, 0
	for i < len(s1) && j < len(s2) {
		if s1[i] <= s2[j] {
			merged[idx] = s1[i]
			i++
		} else {
			merged[idx] = s2[j]
			j++
		}
		idx++
	}
	copy(merged[idx:], s1[i:])
	copy(merged[idx:], s2[j:])
	return merged
}

递归的一分为二，得到归并排序

func MergedSort(s []int) []int {
	if len(s) <= 1 {
		return s
	}
	s1 := s[:len(s) / 2]
	s2 := s[len(s) / 2:]
	s = Merge(MergedSort(s1), MergedSort(s2))
	return s
}

最差时间复杂度：O(nlog n)

堆排序
顾名思义，用堆这种数据结构进行排序，堆是一个近似完全二叉树的结构，并同时满足堆的性质：即任意子结点的键值总是不小于（或者不大于）它的父节点，根节点总是树中的最大值（称为最大堆或大顶堆）或最小值（称为最小堆或小顶堆）

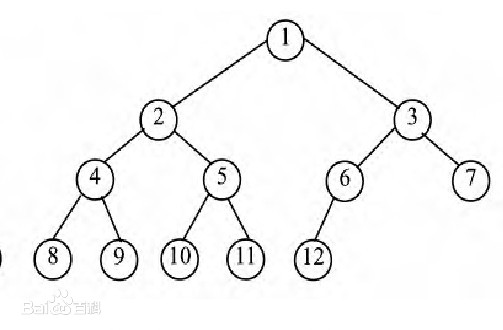
在这里插入图片描述
一般表达二叉树都是使用类似链表的方式，每个节点拥有两根指针，分别指向左子树和右子树，但对于堆来说，它是一个完全二叉树，可以巧妙的使用数组来存储

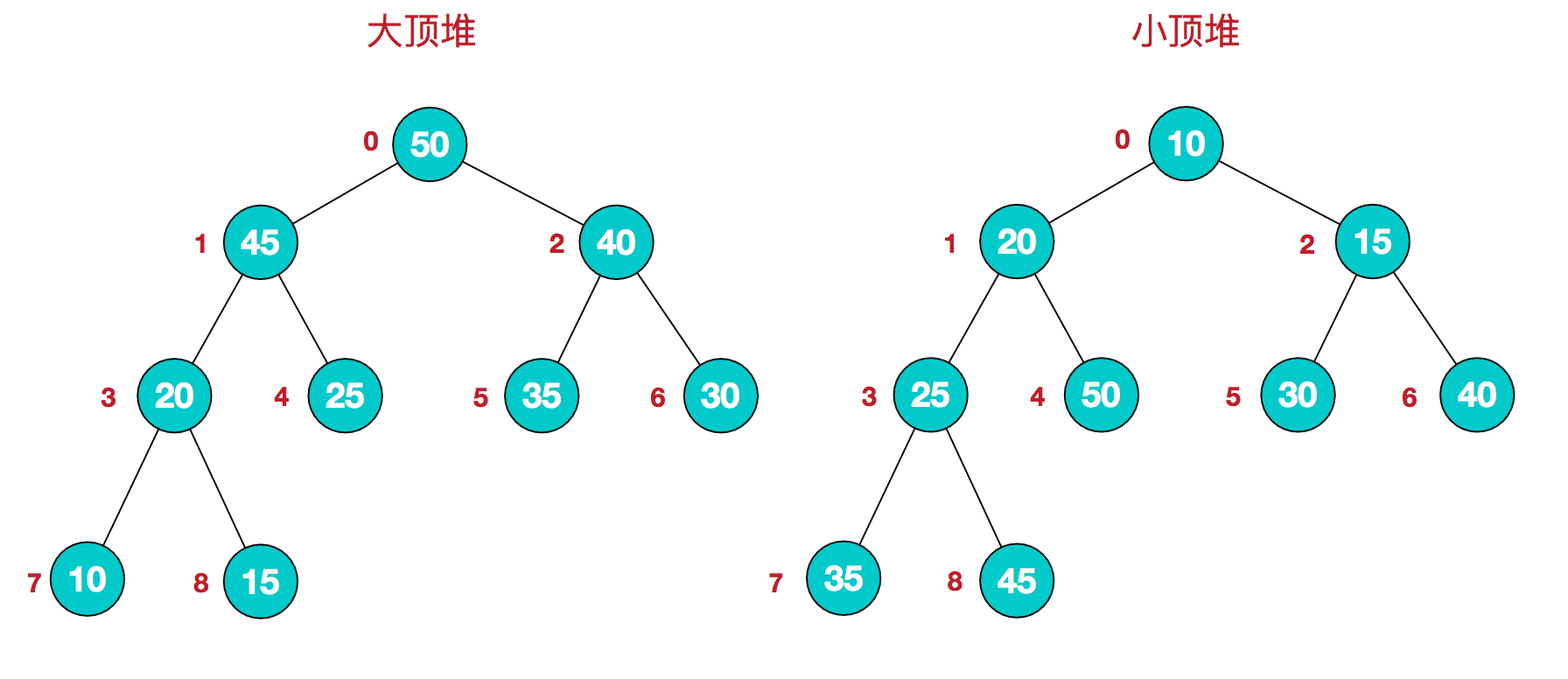
在这里插入图片描述
按层给堆中的每个节点编号，用这个编号作为数组的下标来存储这棵二叉树

在这里插入图片描述
这个数组会满足这样一个特性，任意一个下标为i的元素，它的左子节点在数组中的下标为 2i + 1, 右子节点的下标为2i + 2，它的父节点在数组中的下标为 (i - 1) / 2，比如上图中的 arr[3] = 20，他的父节点是arr[1]=45，它的左子节点是 arr[7]=10，它的右子节点是arr[8]=15。

堆的一般操作有三种：返回堆顶的元素并把它从堆中移除，向堆中新增一个元素，把一个无序数组初始化成一个堆，接下来以大顶堆为例一一介绍（小顶堆类似）

向堆中新增一个元素
首先把这个元素放到数组的末尾，然后用这个元素与它的父节点进行比较，如果比父节点小，则直接满足大顶堆的性质，不需要调整，如果比父节点小，则把它与父节点交换位置，交换位置后，它的父节点要比爷节点（父节点的父节点）小的特性可能就被破坏了，这时，重复对它的父节点进行这样的调整，依此类推，直到满足大顶堆的性质或者到达根节点为止，这种把元素从堆底向上升的调整称为siftup。

type MaxHeap []int

func (heap *MaxHeap) SiftUp(idx int) {
	hp := *heap
	for {
		pIdx := (idx - 1) / 2
		// 到达根节点
		if pIdx < 0 {
			break
		}
		// 当前节点小于父节点，调整完毕
		if hp[idx] <= hp[pIdx] {
			break
		}
		// 比父节点大，与父节点交换位置
		hp[idx], hp[pIdx] = hp[pIdx], hp[idx]
		// 继续看交换后的父节点是不是需要调整
		idx = pIdx
	}
}

func (heap *MaxHeap) Insert(val int) {
	*heap = append(*heap, val)
	if len(*heap) == 1 {
		return
	}
	// 把最尾一个元素进行上升调整
	heap.SiftUp(len(*heap) - 1)
}

简单测试：

func main() {
	heap := &MaxHeap{10, 6, 2}
	heap.Insert(7)
	fmt.Println(*heap)
	heap.Insert(10)
	fmt.Println(*heap)
	heap.Insert(9)
	fmt.Println(*heap)
}

输出：

[10 7 2 6]
[10 10 2 6 7]
[10 10 9 6 7 2]

返回堆顶的元素并把它从堆中移除
把堆中最尾部的元素移到堆顶，然后从堆顶不停向下调整，拿当前节点与它的左右子节点进行比较，如果当前节点不是三者中的最大值，则把当前节点与三者中的最大值进行交换，交换之后继续检查交换后的子节点是否满足堆的性质，重复此步骤直到到达堆的最后一层，这种元素从堆顶向下降的调整称之为siftdown

func (heap *MaxHeap) SiftDown(parentIdx int) {
	hp := *heap
	for {
		childIdx := parentIdx * 2 + 1
		fmt.Println("childIdx:", childIdx)
		// 没有子节点，到达二叉树的最后一层
		if childIdx > len(hp) - 1 {
			break
		}
		// 取左右子节点中较大的值与父节点进行比较
		if childIdx + 1 <= len(hp) - 1 && hp[childIdx] < hp[childIdx+1] {
			childIdx++
		}
		// 左右子节点都不大于父节点，调整结束
		if hp[childIdx] <= hp[parentIdx] {
			break
		}
		// 交换父子节点，继续向下判断
		hp[childIdx], hp[parentIdx] = hp[parentIdx], hp[childIdx]
		parentIdx = childIdx
	}
}

func (heap *MaxHeap) PopTop() (int, error) {
	hp := *heap
	if len(hp) == 0 {
		return 0, errors.New("empty heap")
	}
	max := hp[0]
	if len(hp) > 1 {
		// 把最后一个元素移到堆顶
		hp[0] = hp[len(hp)-1]
	}
	// 释放最后一个元素的空间
	*heap = hp[:len(hp)-1]
	// 从堆顶开始进行下降调整
	heap.SiftDown(0)
	return max, nil
}

测试：

func main() {
	heap := &MaxHeap{10, 10, 9, 6, 7, 2}
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
}

输出

10
10
9
7
6
2
0 empty heap

把一个无序数组调整成一个堆
从这个堆中的倒数第一个父节点（即数组最后一个元素的父节点）开始从右向左，从下到上依次调整各个节点，即执行SiftDown操作，直至根节点为止。

func NewMaxHeap(data []int) *MaxHeap {
	// copy slice
	hp := MaxHeap(append([]int(nil), data...))
	if len(hp) <= 1 {
		return &hp
	}
	// 从数组倒数第一个元素的父节点开始做下降调整 (len(hp) - 1 - 1) / 2
	pIdx := (len(hp) - 2) / 2
	for i := pIdx; i >= 0; i-- {
		hp.SiftDown(i)
	}
	return &hp
}

测试代码：

func main() {
	heap := NewMaxHeap([]int{299, 9, 2, 10, 10, 223, 6, 7, 188})
	fmt.Println("调整后的heap：", *heap)
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
	fmt.Println(heap.PopTop())
}

输出：

调整后的heap： [299 188 223 10 10 2 6 7 9]
299
223
188
10
10
9
7
6
2
0 empty heap

介绍完了堆，回到最开始的堆排序，方法是从数组构造一个最顶堆，每次把堆顶的元素与堆尾的元素进行交换，最大的元素就到了数组的末尾，这样这个数组末尾的元素相当于是排好序了，接下来把待排序的数重新调整成一个最顶堆，然后重复交换最顶堆的元素与堆尾的元素，依次类推，最终就完成了排序。

func HeapSort(s []int) []int {
	heap := NewMaxHeap(s)
	hp := *heap
	for len(hp) > 1 {
		// 把堆顶的元素与堆尾的元素交换
		hp[0], hp[len(hp)-1] = hp[len(hp)-1], hp[0]
		// 数组末尾的元素已经排好序，从堆中移除
		hp = hp[:len(hp)-1]
		tmpHeap := MaxHeap(hp)
		// 做下降调整
		tmpHeap.SiftDown(0)
	}
	return *heap
}

测试：

func main() {
	s := []int{299, 9, 2, 10, 10, 223, 6, 7, 188, -4, 299}
	fmt.Println("排序前：", s)
	fmt.Println("排序后：", HeapSort(s))
}

输出：

排序前： [299 9 2 10 10 223 6 7 188 -4 299]
排序后： [-4 2 6 7 9 10 10 188 223 299 299]