# 递归法获取最大值
class GetMax:
# 求arr中的最大值
def get_max(self, arr):
return self.process(arr, 0, len(arr)-1)
# arr[l...r]范围上求最大值
def process(self, arr, l, r):
# arr[l...r]范围上只有一个数,直接返回
if l == r:
return arr[l]
mid = l + ((r-l) >> 1) # 中点
left_max = self.process(arr, l, mid)
right_max = self.process(arr, mid+1, r)
return max(left_max, right_max)
递归用到了系统栈,如下图。系统栈会记录下一些必要的信息放入系统栈中,返回结果时会将结果返回到栈顶,然后继续执行。
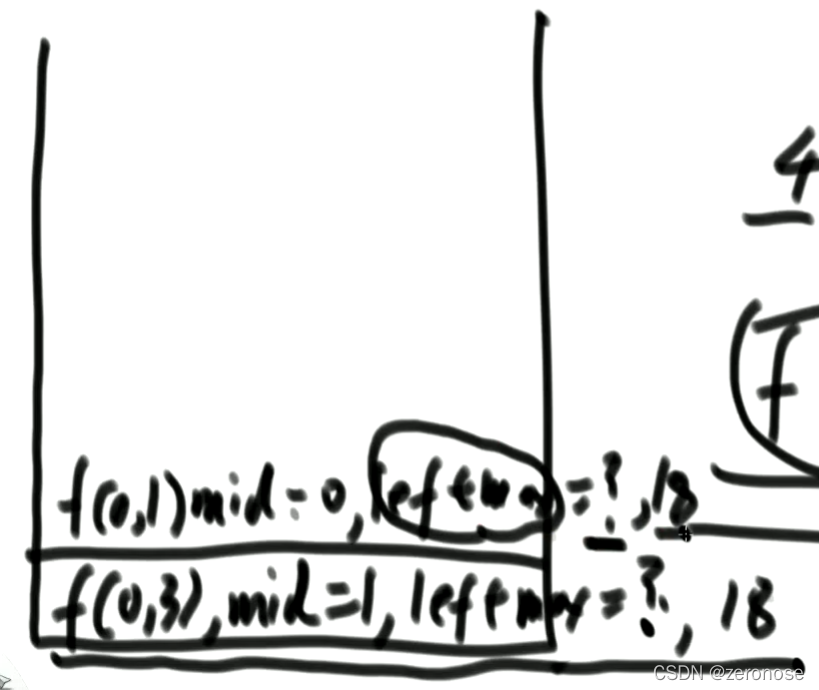
有一种递归是可以直接计算时间复杂度的,如图
只要满足下面公式,其中以上面代码为例,则,a为有几个子过程,此时也就是求left_max 和right_max ,则a=2;b为子过程的范围,也就是N/2 则此时b= 2, d为除子过程外剩下的时间复杂度,此时为常数时间复杂度,也就是O(1)则d=0
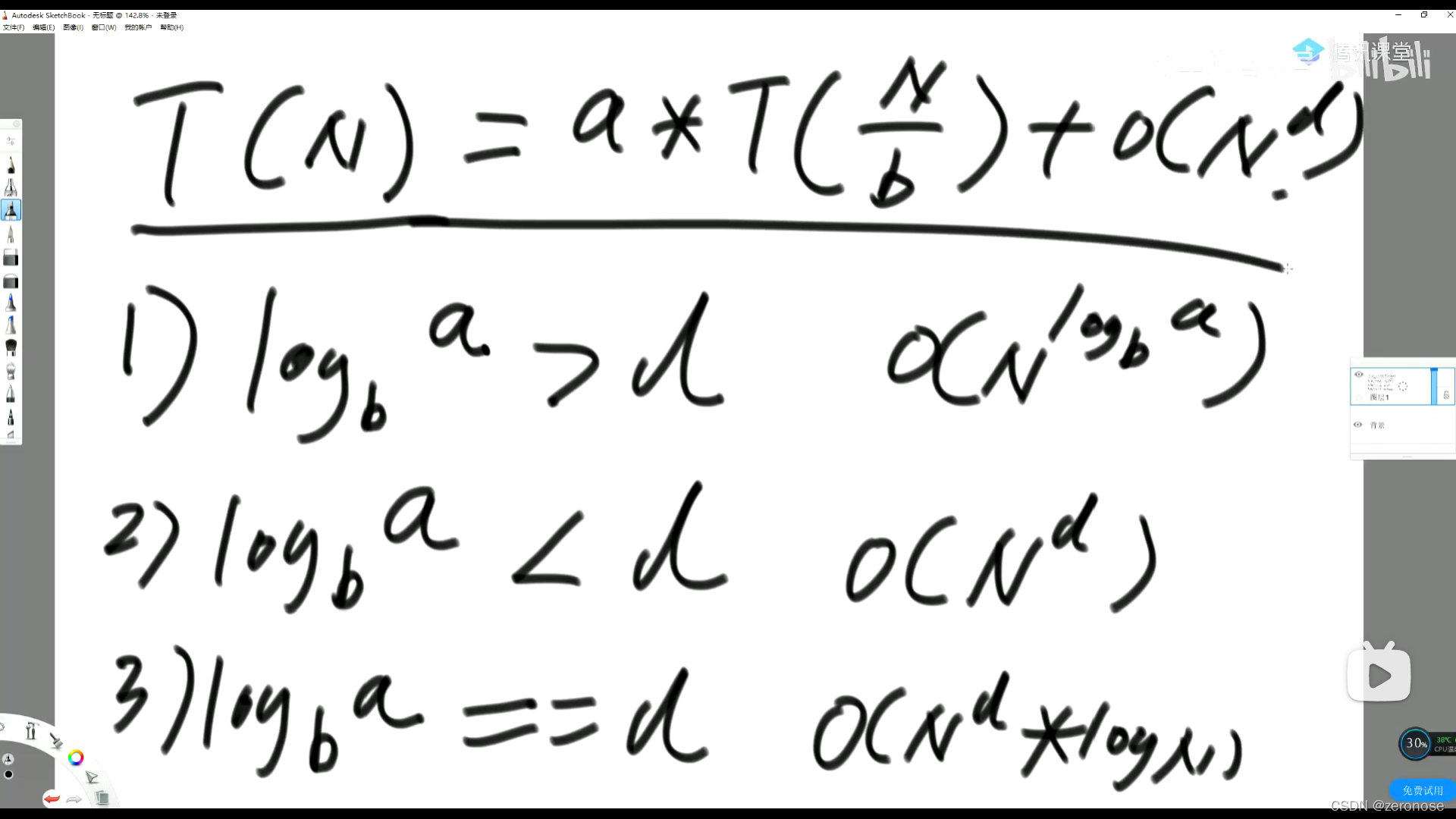





 本文介绍了如何使用递归法获取数组中的最大值,通过类`GetMax`展示了实现过程,包括`get_max`和`process`两个方法。递归过程中,系统栈保存必要的信息,当子问题规模减半时,时间复杂度为O(N/2),最终整个算法的时间复杂度为O(N)。文章还探讨了递归的时间复杂度计算,强调了递归的效率。
本文介绍了如何使用递归法获取数组中的最大值,通过类`GetMax`展示了实现过程,包括`get_max`和`process`两个方法。递归过程中,系统栈保存必要的信息,当子问题规模减半时,时间复杂度为O(N/2),最终整个算法的时间复杂度为O(N)。文章还探讨了递归的时间复杂度计算,强调了递归的效率。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








