自主移动机器人实验项目示例

最新推荐文章于 2025-10-29 11:27:30 发布

原创最新推荐文章于 2025-10-29 11:27:30 发布 · 378 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#移动机器人 #贝叶斯滤波 #扩展卡尔曼滤波 #粒子滤波 #多智能体

第8章实验室实践项目示例

8.1 引言

本章包含多个示例，用于展示本书所介绍的方法在自主移动机器人领域中解决不同问题的应用。本章还包含若干实际示例，进一步演示了这些方法在轮式移动机器人上的较为复杂的应用。每个示例都针对一个特定问题和/或特定的问题解决方法。每个示例的结构如下：首先描述问题，然后详细介绍一种可能的解法，最后展示一些实验结果。这些示例的呈现方式使得感兴趣的读者能够在仿真环境中实现所提出的算法，也可在实际轮式移动系统上实现。因此，实验设计时考虑了所提出的方法可以在一些常见的教育和研究用轮式移动机器人上实现。尽管每个示例都推荐了相应的机器人平台用于算法实现，但也可以考虑其他机器人平台。示例中用于获取真实世界实验结果的轮式移动机器人包括：真空清洁移动机器人iRobot Roomba、配备SICK激光测距仪的研究用移动机器人Pioneer 3‐AT、乐高Mindstorms EV3套件，以及通常用于FIRA微型机器人世界杯足球锦标赛的足球机器人。

这些示例旨在引导读者解决自主移动机器人实现过程中遇到的不同问题。这些示例应激励读者在仿真环境和/或真实的移动机器人上实现所提出的解。由于大多数示例可应用于各种经济实惠的移动机器人，因此这些示例应为读者提供足够的知识，以在相同的机器人平台上重复实验，或对示例进行修改特定的定制移动机器人。这些示例可作为各类自主移动机器人课程实验实践准备的基础。

8.2 基于贝叶斯滤波器的路径与交叉路口网络中的定位

8.2.1 引言

本演示练习展示了如何在已知环境地图中应用贝叶斯滤波器对轮式移动系统进行定位。该练习还涵盖了循线、地图构建以及地图内导航的一些基本原理。假设环境地图由绘制在地面上的线路表示，这些线路代表移动系统可行驶的路径。线路的交点表示十字路口，移动系统可在这些路口选择不同的路径。为简化起见，每个十字路口仅允许两条线路相交，且每对十字路口之间应保持一定的最小距离。

本练习的目标是开发一种能够在相互连接的线路网络（地图）中实现定位并能在地图中的任意位置之间导航的移动系统。相关算法应在配备红外反射传感器的两轮差速驱动移动平台上实现，该传感器用于检测地面上绘制的线路。在本练习的后续部分中，我们将以 Roomba移动系统作为实现平台，但也可使用其他任何具备循线和路口检测能力的移动系统。尽管这只是一个练习，但该问题的适当解法在真实环境中具有实际应用价值，例如在自动化仓库和配送中心中，轮式移动平台被用来在不同站点之间转移对象（包裹）。

该练习由多个部分组成，每个部分开发一个子系统，这些子系统是实现完整定位解所必需的。第一部分致力于实现循线与十字路口选择的控制算法。第二部分涉及里程计算法的实现。第三部分介绍了一种地图构建方法，最后一部分介绍了在地图中进行定位的方法。

8.2.2 循线

第一个任务包括实现用于循线和路口检测的控制算法。在本例中，我们考虑使用红外

示意图0

用于线路检测的光传感器。请思考你认为还有哪些其他传感器也可用于线路检测，以及如何使用。

练习。 首先，编写一个简单的程序，以实现从光传感器读取数据。然后，在地面的不同颜色以及距离地面不同距离的情况下读取传感器数值。根据传感器读数，尝试回答以下问题：在何种情况下可以使用光传感器检测白色背景上的黑线？该传感器是否可用于同时检测地面空洞以及黑白地面？

练习。 编写一个基于光传感器的循线程序。实现循线控制算法需要多少个传感器？使用一个、两个或多个光传感器时，有哪些可能的排列方式可用于实现循线控制算法？你认为哪种设置最具鲁棒性？根据移动系统上光传感器的布局，选择最合适的循线控制算法并加以实现。尝试实现一个简单的开关控制算法以及某种版本的 PID控制器。解释所实现的控制算法相对于其他可能解的优缺点。

练习. 将循线算法扩展以包含路口检测和路径选择算法。当移动系统到达十字路口时，应停止。根据指令（前进、左转、右转、后退），移动系统应选择相应的路径。实现一个用于在十字路口选择四条不同路径的算法。

练习。 根据可用的传感器，实现一些安全机制，以确保移动系统在环境中的安全运行。

iRobot Roomba（500系列）移动系统的底部装有四个光传感器，通常用于检测地面的孔洞（悬崖）。前部两个光传感器可用于线路检测，侧面传感器可用于十字路口检测。图8.1展示了红外传感器如何用于线路跟踪（前方传感器）和十字路口检测（侧面传感器）。

8.2.3 里程计

通过观察车轮旋转，可以使用称为里程计的方法来跟踪移动平台在环境中的位置。假设车轮的旋转由带有计数器 γ的编码器测量。假设当车轮沿前进方向旋转时，编码器计数器的值增加，而当车轮反向旋转时，计数器的值减少。

示意图1

当轮子朝相反方向旋转时，计数器递减。计数值的时间差 γ(k )= γ(k) − γ(k − 1)与轮子的相对旋转成正比。根据左 γL(k)和右 γR(k)编码器的计数值时间差，可分别计算出左 ϕL(k)和右 ϕR(k)轮子的相对旋转：

ϕL(k) ∝γL(k) ϕR(k) ∝γR(k) (8.1)

移动系统位姿(x(k),y(k), ϕ(k))可通过轮式移动系统的正向运动学模型的一阶差分欧拉积分法的离散解进行近似：

x(k+ 1)= x(k)+d(k) cos ϕ(k) y(k+ 1)= y(k)+d(k) sin ϕ(k) ϕ(k+ 1)= ϕ(k)+ϕ(k) (8.2)

移动系统的相对距离 d(k) 和相对旋转 ϕ(k) 可以通过车轮的相对旋转来确定：

d(k)= r 2(ϕR(k)+ϕL(k))

ϕ(k)= r L(ϕR(k) −ϕL(k)) (8.3)

其中L是轮距，r是车轮半径。

练习。 实现里程计算法。读取左轮和右轮的编码器值，实现里程计算法，并

练习。 校准里程计模型参数。提出一种基于使用外部测量设备在两个不同时间点测量移动系统位姿的校准程序。如有必要，需考虑编码器计数器溢出。确定不引起车轮打滑的移动系统最大允许切向速度和角速度。

练习。 根据精度评估已实现的里程计算法的性能。该里程计模型（8.2）是通过对一阶差分进行离散欧拉积分得到的。尝试使用一种更精确的离散里程计模型，重新实现里程计算法，并比较结果。

练习。 里程计能够估计移动系统的位姿；因此，当移动系统绕垂直旋转轴旋转时，也能够利用它来估计旋转角度。由于假设十字路口的四条路径以90度角相交，因此可以在路径选择算法中使用里程计。如有需要，可利用里程计提供的旋转测量结果，改进上一节中实现的路径选择算法。

在图8.2 中展示了通过里程计获得的路径的一个示例。

8.2.4 地图构建

本节介绍了一种用于地图构建的半自动监督方法。地面上绘制的线条在多个交叉路口相交，例如图8.3所示。为简便起见，我们假设所有交叉路口均连接四条路径，并且所有路径的两端均连接至交叉路口。相邻交叉路口之间的路径形状可假设为任意形状。我们将所有

K个十字路口标记为集合 K={Ki}i=1,2,…,K，将所有P条直连路径标

记为集合P={pi}i=1,2,…,P。每条路径被赋予一个主导方向：若路径

pi的方向是从十字路口Kj到Kl，则路径 ¯pi的方向为相反方向，即

从十字路口Kl到Kj。非主导路径¯被归入集合 P={¯pi}i=1,2,…,P。

以图8.3为例，共有K= 3个十字路口，标记为集合 K={A, B, C}，以及P= 6条直连路径，标记为集合 P={a, b, c, d, e, f}。因此，交叉路口和路径的空间表示可以表示为一个图，如图8.3右侧所示。

示意图2

当将地图的空间表示重绘为图形式时，连接（路径）到节点（十字路口）的顺序应与真实地图中的顺序保持一致。

为了能够在移动系统从任意路径进入十字路口时确定哪条路径位于左、右和直行方向，这是必需的。另一种方法是将十字路口中路径的顺序保存在表格中，如表8.1所示，其中列出了路径的位置

表8.1 节点（交叉路口）中的连接（路径）

Node	A	B	C
连接	a, f, ¯e, ¯a	b，d	f¯, ¯b

表8.2 连接（路径）的终点节点（交叉路口）

连接	a	b	c	d	e	f
节点	A, A	B, B	C, C	B, C	C, A	A, B

可以根据路径的有序列表确定十字路口。所有直接连接的终止节点也可以用表格形式表示（表8.2），其中节点的顺序对于区分主导和非主导路径方向非常重要。因此，整个地图可以表示为图或等效表格的形式；这些数据结构在计算机内存中易于实现。

当前以图（或表格）形式表示的地图中，交叉路口（节点）之间的空间关系以及路径（连接）的形状都丢失了。由于我们假设所有交叉路口的形状相同（四条路径相互垂直），因此当知道交叉路口之间所有直接路径的形状后，就可以重建整个地图。所有直接路径的形状可以通过里程计过程记录（图8.4）。尽管里程计过程存在一些明显的缺点，但它足以确定

示意图3

两个节点之间路径的近似形状。因此，如果至少部分路径的形状存在足够差异，则应能够基于已存储的地图数据（地图的图表示以及所有直接路径的形状）来确定移动系统在地图中的位置。环境地图通过一组交叉路口K、一组路径 P以及通过里程计过程记录的路径形状来表示。在地图构建过程中，所有这些信息都需要写入适当的数据结构并保存在非易失性存储区域中。

练习。 为所有交叉路口分配节点标签，并使用连接标签标记所有路径。绘制地图的图形表示，并以表格形式呈现该图。选择合适的数据结构来表示地图的图形表示，并将地图插入代码中。所选数据结构应能够存储具有不同数量交叉路口和路径的地图。

练习。 使用里程计记录所有直接路径的形状（图8.5）：将移动系统放置在起始路口的路径起点，让移动系统沿线行驶直到下一个（终点）十字路口，保存所记录的路径形状，并对所有其他路径重复此操作。环境地图应保存到非易失性存储区域（例如，作为文本文件保存在硬盘上）。

练习。 编写一个程序，将地图构建过程自动化到适当程度。

8.2.5 定位

本节介绍了一种在上一节构建的地图中进行定位的算法。定位的目标是确定移动系统当前所行驶的路径、行驶方向（从起始节点到终止节点）以及距离起始节点或终止节点的距离。

假设移动系统通过循线沿路径行进，并在交叉路口随机选择下一条路径。通过将当前里程计数据与地图中存储的里程计数据进行比较，移动系统应能够在地图内实现定位。定位的基本概念如下：将交叉路口之间路径的当前里程计数据与地图中存储的所有里程计数据进行比较，基于预定义的拟合优度，计算所有路径的概率。

一旦某条路径的概率明显大于所有其他路径的概率，移动系统的位置即被视为已知（具有一定概率）。

定位问题可以通过贝叶斯滤波器的框架来解决。为了实现简单起见，假设定位算法仅在移动系统到达一个新的交叉路口时执行一次，即在选择下一条路径之前。因此，如果已知移动系统是从哪条路径到达该十字路口的，则其位置是已知的。由于每条路径都有两个方向，我们需要考虑所有直接路径在两个方向上的概率。对于每条路径¯xk ∈ P⋃P，需要计算以下置信函数：

belp(xk)= ∑ xk−1 ∈ P⋃ P¯ p(xk|xk−1, uk)bel(xk−1) (8.4)

bel(xk)= 1 ηkp (zk|xk)belp(xk) (8.5)

其中ηk=∑xk∈ P⋃ P¯ p(zk|xk)belp(xk)。

假设在到达第一个十字路口时首先执行定位算法。在初始步骤中，移动系统的位置未知；因此，所有路径的概率均相同。移动系统根据给定的控制动作（前进、左转、右转或后退）以任意方向离开十字路口。路径选择控制算法被认为以一定概率选择目标路径。

十字路口中的所有出口路径可以用标签s1, s2, s3,和s4标记，如图 8.6所示。需要确定当当前路径为路径之一{s}1, ¯s2, ¯s3,和 ¯s4时，选择路径s1在所有可能的控制动作下的概率。例如，对于控制动作前进，其概率可能如下：

p(Xk= s1|Xk−1= ¯s1, Uk=f orward)= 0.05 p(Xk= s1|Xk−1= ¯s2, Uk=f orward)= 0.1 p(Xk= s1|Xk−1= ¯s3, Uk=f orward)= 0.75 p(Xk= s1|Xk−1= ¯s4, Uk=f orward)= 0.1 (8.6)

练习。 根据路径选择算法的鲁棒性，确定当当前路径是路径X k−1 ∈{¯s1, ¯s2, ¯s3, ¯s4}之一时，针对所有可能的控制动作Uk ∈{前进,左,右,后退}，选择路径Xk= s1的概率p(xk|xk−1,uk)。

示意图4

由于交叉路口是对称的，因此假设以下关系成立：

对于所有出口路径，可以将其对应的入口路径写成表格形式，这在实现定位算法时非常方便（见表8.3）。

移动系统随后离开十字路口，沿线路行进并记录里程计数据，直到检测到下一个十字路口。当移动系统到达下一个十字路口时，将上一个与当前十字路口之间记录的里程计数据与地图中已存储的所有里程计数据进行比较，以确定概率p(zk|xk) 的某个距离度量

表8.3 图8.3示例中所有出口路径的入口路径Fig. 8.3

s1	a	b	c	d	e	f	a¯	b¯	c¯	d¯	e¯	f¯
¯s1	¯a	¯b	¯c	¯d	¯e	f¯	a	b	c	d	e	f
¯s2	a	b	c	¯b	¯c	¯a	e	f	d	¯e	f¯	¯d
¯s3	e	f	d	b	c	a	f¯	¯d	¯e	¯c	¯a	¯b
¯s4	f¯	¯d	¯e	f	d	e	¯a	¯b	¯c	c	a	b

比较里程计数据的形状需要定义。因此，最可能路径是距离值最小的路径。

练习. 定义一种距离度量方法，用于比较通过里程计获得的路径。需考虑移动系统可能并非以恒定速度沿路径行驶的情况。通过实验评估所选距离度量的性能。

在图8.7 中展示了路径比较度量定义的一种思路。可以定义不同的距离度量，例如：SASE= 1 m∑ m i=1 √(xi − xo,i)2+(yi − yo,i)2或 SSSE=1m√∑ m 度量也在图8.8中展示）。

现在可以更新公式(8.5)中的置信函数。置信分布的演化过程如图8.9所示。在初始步骤中，所有路径的概率相等（图8.9A）。当移动系统行驶过两个路口之间的第一条路径后，基于测量数据计算各路径的概率（图8.9B），并更新置信函数（图8.9C）。经过若干步骤后，当移动系统经过多个路口时，根据置信函数得出的最可能路径应为实际路径。

练习。 实现基于贝叶斯滤波器的定位算法。

练习扩展定位功能，以报告移动系统在路径上的位置相对于起始路口的相对距离。

练习。 尝试改进定位算法，使得路径置信分布在交叉路口以及路径跟踪过程中都能得到更新。

练习. 实现一种从地图内任意位置到目标终点位置的路径规划算法。实现控制移动系统沿地图行驶至目标终点位置的控制算法

示意图5

示意图6 初始置信分布，(B) 第一次测量的概率分布，以及( C) 第一次更新后的置信分布和(D) 多次更新后。)

8.3 基于扩展卡尔曼滤波器的室内全球定位系统与里程计融合定位

8.3.1 引言

移动机器人通常需要能够在环境中进行定位，以自主执行某些期望的任务。为了使移动系统具备定位能力，必须为其配备适当的传感器，该传感器能够确定移动系统相对于外部（全局）坐标系的位置。

这可以通过多种方式实现。本练习考虑一种从外部测量系统获取位置的定位方法。在室外环境中，可以使用全球导航卫星系统（ GNSS）来确定全球位置，该系统如今在全球范围内都可用（精度可能有所不同）。由于GNSS无法在室内环境中工作，因此已开发出一些特殊的室内定位系统。其中一些系统基于测量多个静态传输点之间的无线网络信号强度或飞行时间，而另一些则使用基于图像的物体跟踪技术。全球定位系统通常仅测量位置，而不测量被跟踪物体的姿态。然而，对于自主导航的实现，轮式移动系统必须清楚其位置和姿态。

8.3.2 实验设置

本练习涵盖如何基于里程计数据以及移动系统在环境中的位置测量来估计轮式移动机器人在空间中的位姿。所考虑的实验设置（图 8.10）包括一个配备有轮编码器和测量单元的轮式移动系统，该测量单元能够确定安装在移动系统顶部的标签相对于环境中位置固定且已知的锚节点的位置。将使用差速驱动的移动机器人（第2.2.1节）；然而，所提出的方法也可用于其他任何类型的轮式移动驱动系统。

该实验设置包含一个在每个轮子上都装有旋转编码器的轮式移动系统。

示意图7

根据编码器读数，可以采用里程计方法来估计移动系统位姿。

由于通过里程计获得的位姿容易产生漂移，因此必须利用外部位置测量对位姿估计进行校正。移动系统的位置通过室内定位系统获取，但该测量系统的精度有限。这是一个传感器融合问题，针对给定的设置，可以在扩展卡尔曼滤波器（EKF）的框架下解决。一旦定位算法被实现并调整完毕，就可以将移动系统扩展为能够在环境内的目标位置之间进行自主导航。

8.3.3 扩展卡尔曼滤波器

此处考虑使用扩展卡尔曼滤波器（EKF）来解决移动系统定位问题。 EKF（第6.5.2节）是传统卡尔曼滤波器在非线性系统中的扩展，通过对协方差矩阵进行线性近似实现。该算法具有两步结构：基于当前动作对状态进行预测（公式6.38），以及在新的系统输出测量可用时对预测的状态进行校正（公式6.39）。为了实现EKF，必须提供系统的模型和噪声模型。系统的非线性模型（6.37）必须

在当前估计状态附近线性化，以获得矩阵（6.40）–（6.42）。实现扩展卡尔曼滤波器最具挑战性的部分是对系统运动学和噪声进行适当的建模，这些噪声由各种过程产生。噪声通常依赖于时间或状态，难以测量和估计。

预测步骤

让我们建立一个考虑系统不确定性的运动学里程计模型。机器人的车轮配备了编码器 γL和 γR，分别用于跟踪左轮和右轮的姿态。假设左轮和右轮的相对编码器读数 γ{L,R}(k)= γ{L,R}(k) −γ{L,R}(k − 1)与车轮角速度 ω{L,R}(k) ∝ γ{L,R}(k)成正比。假设每个轮子的旋转编码器读数 γL和 γR受到加性白噪声wT(k)=[wγL(k)wγL(k)]的干扰。区分用希腊字母 ω表示的角速度和用字母w表示的噪声。该噪声被认为不仅包含测量噪声，还包括由各种来源引起的噪声影响，如车轮打滑。因此，假设编码器读数 γˆ{L,R}(k)与真实的编码器值 γ{L,R}(k)之间的关系如下：

[ γˆL(k) γˆR(k)]=[γL(k) γR(k)]+[wγL(k) wγR(k)] (8.8)

假设噪声的分布为均值为零的正态（高斯）分布，w(k)∼N(0,Q)。

对于扩展卡尔曼滤波器的应用，噪声分布不必为正态分布，但噪声应是无偏的。假设噪声协方差矩阵Q为对角矩阵，因为假设轮子噪声之间不存在交叉相关性：

Q=[σ 2 γL 0 0 σ 2 γR] (8.9)

根据相对编码器读数 γˆ{L,R}(k)，可以确定轮式移动系统的相对纵向 ˆ行驶距离 d(k) 和相对旋转 ϕˆ(k)：

ˆd(k)= rα γˆR(k)+ γˆL(k) 2 ϕˆ(k)= rα γˆR(k) − γˆL(k) L (8.10)

差速驱动的离散运动学模型（公式2.3）可以写成以下形式：

xˆ(k+ 1)= xˆ(k)+ˆd(k) cos ϕˆ(k) yˆ(k+ 1)= yˆ(k)+ˆd(k) sin ϕˆ(k) ϕˆ(k+ 1)= ϕˆ(k)+ ϕˆ(k) (8.11)

由于车轮受到噪声干扰，使用递归估计方法（公式8.11）估计的轮式移动系统位姿容易产生漂移。

练习。 将公式(8.8)和(8.10)合并为公式(8.11)。将公式(8.10)中的项γ{L,R}(k)代入公式(8.8)，并将公式(8.11)中的项 d(k)和 ϕ(k)代入公式(8.10)。

练习基于公式(8.10)和(8.11)，实现里程计算法。有关实际实现建议和注意事项，请参考第8.2.3节中的描述并完成其中的练习。设计并描述一种对里程计算法参数进行校准的流程。第8.2.3节

里程计算法中的参数（T、r、L和α ）均可测量。然而，实现里程计算法只需知道参数Trα和L。这两个参数可通过适当的校准程序获得。例如，可使移动系统沿圆弧运动，若已知该圆弧的长度和相对旋转，则可根据两个方程（8.10）求得参数Trα和L。

无噪声的轮式里程计运动学模型（公式8.11）可用于对移动系统位姿进行预测，因此可应用于扩展卡尔曼滤波器的预测步骤中。

在扩展卡尔曼滤波器的预测步骤中，基于前一时间步的状态估计（使用非线性系统模型，本例中为无噪声的公式8.11）来预测系统的新的状态（移动系统位姿），同时还要计算新的协方差矩阵（通过对系统在前一估计值附近的线性化得到）。

练习。 使用模型（8.10），推导雅可比矩阵（6.40）和（6.41），并计算在扩展卡尔曼滤波器算法的预测步骤（6.38）计算中所需的矩阵F(k)QF T (k)。

扩展卡尔曼滤波器预测步骤中所需的雅可比矩阵由公式(6.40)、(6.41) 确定，如下所示：

A(k)= ⎡⎣1 0 −TrαγD(k)+γL(k) 2 sin ϕ(k) 0 1 2 cos ϕ(k) 0 0 1 ⎤⎦

F(k)= Trα 2L ⎡⎣L cos ϕ(k) L cos ϕ(k) L sin ϕ(k) L sin ϕ(k) −2 2 ⎤⎦ (8.12)

考虑到输入噪声协方差矩阵（8.9），式（6.38）中出现的矩阵FQFT为

F(k)QF T(k)= T2r2α2(σ 2 γR+σ 2 γL) 4 ⎡⎣ cos2 ϕ(k) cos ϕ(k) sin ϕ(k) 0 cos ϕ(k) sin ϕ(k) sin2 ϕ(k) 0 0 0 4 L2 ⎤⎦ + T2r2α2(σ 2 γR − σ 2 γL) 2L ⎡⎣ 0 0 cos ϕ(k) 0 0 sin ϕ(k) cos ϕ(k) sin ϕ(k) 0 ⎤⎦ (8.13)

考虑到公式（8.9）中所有对角元素的方差彼此相等，因此公式（8.13）的最后一项为零。

示意图8 相图 y(x)，(B) 相图 ϕ(x) 和 (C) 相图 ϕ(y)。底部行：状态的时间演化及一个标准差的误差方差范围：(D) 信号 x(t)，(E) 信号y(t) 和 (F) 信号 ϕ(t)。)

图8.11显示了仿真结果，其中对机器人施加了恒定输入速度。在图 8.11的底部行显示了状态预测的时间演化及一倍状态误差协方差边界标准差。图8.11 的顶行显示了预测路径（广义机器人坐标的二维投影）以及最终状态的投影状态误差协方差矩阵的等高线。顶行中的图表还显示了在多次重复模型仿真并添加模拟噪声后得到的最终状态的预测云。注意最终状态云与估计的误差协方差矩阵（椭圆）之间的不同形状。

练习. 在仿真环境中和实际移动系统上实现扩展卡尔曼滤波器的预测步骤。在仿真环境中评估状态预测性能，绘制系统位姿，并绘制协方差元素随时间的变化函数，如图8.11所示。

练习。 假设将白噪声独立地添加到信号ˆd和 ϕ，而不是信号 γL和 γR，即 d= d+wd和 ϕˆ= ϕ+ wϕ。计算新的状态误差协方差方程，并修改状态预测算法。注意，在这种情况下，协方差矩阵Q中的数值具有不同的含义。

校正步骤

一旦获得系统输出状态的新测量值，就可以在校正步骤（6.39）中更新当前状态估计。为了能够更新系统状态，需要确定一个系统输出模型。

h(k)=[cos ϕ(k) −sin ϕ(k) cos ϕ(k)][ssxy] +[xy]+[vvxy] (8.14)

测量噪声v=[vx vy]可以建模为具有零均值和高斯分布的白噪声，v ∈N练(0习,R。)。根据测量模型（8.14），计算式（6.42）中定义的雅可比矩阵C(k{v16}。考虑噪声协方差矩阵R的三种形式：正定对称矩阵、具有正元素的对角矩阵，以及所有元素均为正且相等的对角矩阵。对于你的问题，哪种形式的协方差矩阵最合适？如果噪声协方差矩阵是在移动机器人局部坐标系中给出，而不是在全局坐标系中给出，该模型将如何变化？

雅可比矩阵C(k)由非线性测量模型（8.14）确定，如下所示：

C(k)=[1 0 −sx sin ϕ(k) − sy cos ϕ(k) 0 1 sx cos ϕ(k) − sy sin ϕ(k)] (8.15)

通常我们可以假设一个对角测量噪声协方差矩阵：

R(k)=[σ v2x 0 0 σ v2y] (8.16)

其中σ v2x和 σ v2y分别为沿x和y方向的测量噪声方差，通常二者相等。

如果噪声信号vx(k)和vy(k)之间存在显著相关性，则应采用噪声协方差矩阵R的一般形式。在特殊情况下，当传感器安装在移动系统的旋转中心时（sx= 0和sy= 0），模型（8.14）得以简化，雅可比矩阵C(k)的最后一列变为零，因此所有测量雅可比矩阵均变为恒定单位矩阵。

练习。 根据式(6.39)所述，实现EKF的校正步骤，并通过评估位置传感器特性来确定测量噪声协方差矩阵的值。

精确的噪声建模是实现扩展卡尔曼滤波器中最关键的部分之一。

假设每个轮子上的噪声方差依赖于轮速，因此满足以下关系σ 2 ω{L,R}( k)= δω2 {L,R}(k)，从而得到[1]：

Q(k)=[δω2 L(k) 0 0 δω2 R(k)] (8.17)

在此噪声模型中，参数 δ 定义了相对于轮速的噪声比例。

**练习。

第8章实验室实践项目示例

8.3 基于扩展卡尔曼滤波器的室内全球定位系统与里程计融合定位

8.3.3 扩展卡尔曼滤波器

校正步骤

练习。 修改EKF算法以使用噪声模型（8.17）。根据系统噪声特性调整模型参数。评估改进后EKF算法的性能。

估计路径的一个示例如图8.12所示。尽管初始位姿估计有误，定位算法仍收敛到真实的移动机器人位姿。该滤波器还能估计移动机器人航向，而航向无法直接从全球定位系统获得。虽然航向可以通过位置测量值的微分来确定，但在存在噪声的情况下，若无适当的信号预滤波，这种方法极不可靠，而预滤波会引入滞后。因此，如本例所示，更推荐采用卡尔曼滤波方法。

练习。 作为附加练习，实现一个简单的控制算法，使机器人能够在环境中自主导航至任意目标。使用额外的接近传感器来检测障碍物，并尝试实现一个避障算法。

示意图9

8.4 基于粒子滤波的彩色瓷砖图案定位

8.4.1 引言

定位是轮式自主机器人中最基本的问题之一。该问题通常在贝叶斯滤波器的框架下解决。在各种滤波方法（卡尔曼滤波器、扩展卡尔曼滤波器、无迹卡尔曼滤波器等）中，粒子滤波器[2]正受到越来越多的关注。本练习将展示如何使用粒子滤波器来解决轮式移动机器人在由彩色瓷砖构成的平面上的定位问题。

8.4.2 实验设置

该轮式移动机器人配备了轮编码器和颜色传感器，可检测机器人下方表面的颜色（图8.13）。假设该移动机器人采用差速驱动，轴长为L，轮半径为r。颜色传感器在机器人上的安装位置相对于机器人的旋转中心在纵向和横向方向分别偏移了sx和sy。地面由大小相同的正方形彩色瓷砖铺成，覆盖了一个M ∈ N乘以N ∈ N块瓷砖的矩形区域。移动机器人只能在由墙壁边界围成的瓷砖区域内移动。

瓷砖共有C ∈ N种不同颜色。地面上彩色瓷砖的布局（即地图）是已知的。图8.14 展示了一个

示意图10

示意图11

尺寸为 180× 100 cm2,的环境，其中M= 10，N= 18，以及L= 6。该考虑的设置可以使用乐高Mindstorms EV3套件中提供的元件构建，本示例中也使用该套件获取一些真实世界的数据。

练习。 准备一个带有彩色瓷砖的平面，移动机器人可以在其上移动。创建一个可以放置方形瓷砖的矩形网格。用墙壁边界围住该矩形区域，以防止移动机器人离开工作区域。选择一组多种可区分颜色用于彩色瓷砖，并将这些颜色随机分布在平面上的网格中（图8.14）。彩色瓷砖可以打印或涂绘在地面上，也可以使用方形彩色贴纸。

练习组装一个机械可工作的移动机器人，使其能够在平坦环境中移动；建议使用差速驱动。将颜色传感器安装在距离地面适当的位置，以可靠地检测地面上方块的颜色。移动机器人的设计示例如图8.13所示。

8.4.3 手动控制

本练习涉及定位算法的实现。因此，只需手动操作移动机器人即可，但一旦实现了定位算法并对其进行评估后，还可以开发一些自动行驶控制算法。

练习。 为了在表面上驱动移动机器人，请编写一个简单的程序，通过键盘或其他操作员输入设备对移动机器人进行远程控制。基于轮编码器提供的反馈实现轮速控制。设计控制算法时，应允许设置机器人期望的切向和角参考速度，而不是仅设置车轮的期望参考速度。对于EV3电机，电机速度控制已经实现，只需启用即可。

8.4.4 轮式里程计

轮式里程计是一种基本的定位方法，可在已知初始位姿的情况下用于估计移动机器人位姿。众所周知，由于车轮打滑，该方法容易产生漂移，但在短距离内的误差通常相对较小。如果有位置的附加信息可用，则可以消除漂移；本文考虑使用颜色传感器。基于轮式移动机器人的内部运动学模型的估计运动通常用于每个基于贝叶斯滤波的定位算法（包括粒子滤波器）的预测步骤中。轮式里程计通常基于增量编码器测量实现（乐高Mindstorms EV3套件中的电机均配备有编码器）。为了

为了微调里程计算法的参数（轮半径和轴长）以适应特定的轮式移动系统设计，通常需要采用适当的校准方法。

练习基于轮编码器读数实现里程计。务必正确校准并评估里程计精度。请遵循第8.2.3节中给出的里程计实现说明和提示。

8.4.5 颜色传感器校准

里程计漂移可以通过轮式移动机器人下方地砖颜色的读数来消除，因为假设已知彩色瓷砖的布局（环境地图）。为了检测表面颜色，需要使用颜色传感器（Mindstorms EV3套件包含一个颜色传感器）。假设单次颜色传感器测量被编码为RGB三元组，即RGB颜色空间中红色、绿色和蓝色分量的值。该颜色传感器需要能够区分构成地面表面的C种不同颜色的方块。为此，原始传感器读数（RGB值）需要被分类到C个颜色类别之一（可额外定义一个类别用于其他任何颜色）。颜色传感器需要针对其在移动机器人上的具体安装方式以及地面表面进行校准。通常，在HSV（色调‐饱和度‐明度）色彩空间中实现鲁棒的颜色分类比在RGB颜色空间中更简单。因此需要使用 RGB到HSV颜色转换（公式5.87）。图8.15 显示了六种不同颜色瓷砖的颜色读数在HSV色彩空间中明显可分。

练习编写一个读取颜色传感器数据的程序。使用公式(5.87)将获得的原始RGB值转换为HSV色彩空间。对相同颜色进行多次测量，并将所有颜色的读数用类似图8.15所示的图表示。评估传感器读数对光照变化和相对于地面表面的小位姿扰动的敏感性。根据传感器读数在必要时重新调整传感器的位置。也可添加一个保护罩，以防止外部光照变化对传感器的影响。基于收集到的颜色测量数据，实现一种颜色聚类算法。可以确定一组规则，用于实现颜色的聚类，即这些规则应定义聚类边界。确保规则的设定使得聚类边界足够宽，以便在不同光照条件下仍能检测到颜色，但又足够窄，以防止在颜色过渡时发生误分类。

示意图12

8.4.6 粒子滤波器

颜色传感器测量值和里程计数据提供了关于轮式移动机器人全局位姿的部分信息。可以使用粒子滤波器来融合来自不同来源的信息，以获得对机器人位姿更准确的状态估计。单独的颜色传感器无法直接提供移动机器人航向的信息，但在粒子滤波器的框架下，它可以用于消除里程计漂移并实现全局定位，即无需预先知道移动机器人的初始位姿。粒子滤波器的基本思想是用一组粒子来近似状态估计的概率分布。在此情况下，粒子代表了对轮式移动机器人位姿的假设。该算法包括多个步骤：粒子初始化、预测、重要性重采样以及基于粒子分布评估最可能的轮式移动机器人位姿。算法的各个步骤如图8.16 所示（工作区域比图8.14 中的小，以便提高可见性）。

练习. 尽管不是必需的，但编写一个程序将所有传感器数据（里程计和颜色测量）及控制动作记录到文件中。这可以简化粒子滤波器的开发，因为算法可以在离线状态下进行开发。相同的数据可在算法测试、调试和调优过程中多次使用。为此目的，简单的逗号分隔文件格式已足够。然后驱动机器人

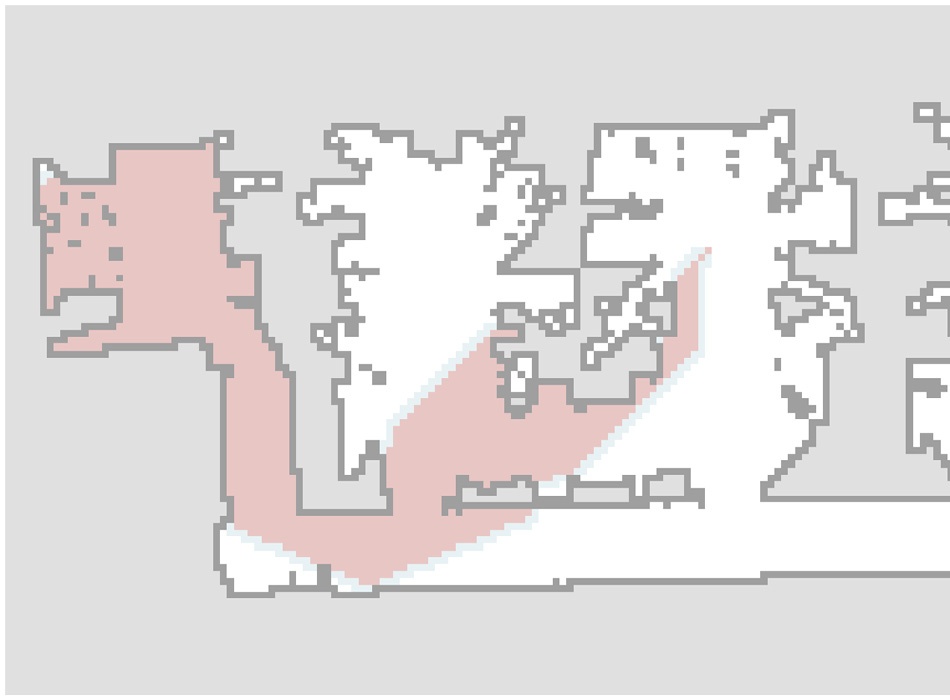示意图13 粒子初始化，(B) 预测步骤，(C) 重要性重采样，(D) 最可能机器人位姿的评估，(E) 第二次迭代，(F) 第三次迭代，(G) 第四次迭代，以及 (H) 更多次迭代之后的结果。实线多边形表示真实机器人位姿（彩色圆圈为当前传感器读数），虚线多边形为估计的机器人位姿，黑色箭头为粒子。)

在操场周围收集传感器数据。编写一个程序以实现加载已存储的数据。

在粒子滤波器初始种群N ∈ N的初始步骤中，需要确定粒子。在特定情况下，每个粒子代表关于轮式机器人位姿的一个假设，即第i个粒子表示可能的机器人位置和航向qiT=[xi, yi, ϕi]。粒子应根据轮式机器人位姿的初始概率分布进行分布。当初始机器人位姿未知时，可以使用均匀分布，即粒子应在整个状态空间内均匀分布。图8.16A 显示了粒子的初始均匀分布。

练习。 实现粒子滤波器的初始化步骤。

轮式移动机器人随后可以进行移动。该算法的第一步是粒子的预测。每个粒子根据假设的移动机器人位姿变化进行更新。这通常依据基于里程计数据的估计的位姿变化d(k)和ϕ(k)，这

对于第i个粒子，更新方程如下（采用差速驱动运动学模型的简单欧拉积分）：

xi(k+ 1)= xi(k)+d(k) cos(ϕi(k)) yi(k+ 1)= yi(k)+d(k) sin(ϕi(k)) ϕi(k+ 1)= ϕi(k)+ϕ(k) (8.18)

可以向每个粒子的预测位姿估计添加具有适当分布的随机生成的噪声，以建模扰动，例如车轮打滑。在粒子预测之后，粒子的预测分布如图8.16B所示。

练习实现粒子滤波器的预测步骤。观察移动机器人行驶时对粒子的评估。评估添加到预测粒子状态中的不同随机噪声水平的影响。

然后测量移动机器人下方地砖的颜色。为简化起见，假设颜色传感器位于移动机器人的旋转中心（sx= 0和s y= 0）。通过将测量的颜色与各个粒子下方的地砖颜色进行比较，利用传感器测量结果来确定每个粒子的重要性。与测量结果一致的粒子将获得较高的重要性评分，而其他粒子则获得较低的评分。特定粒子的评分可根据其到最近同色地砖的距离来确定，该颜色需与传感器测得的颜色相同。

练习。 使用测得的传感器数据来确定每个粒子的重要性。

每个粒子的重要性被用于粒子重采样步骤中。粒子以随机采样的方式被选择，其中从一组粒子中选择特定粒子的概率与其重要性评分成正比。因此，具有较重要性评分的粒子预期会被更多次选中。重采样步骤后粒子的更新后分布如图8.16C.所示

练习. 根据确定的重要性分数实现粒子重采样。

最后一步是对粒子进行评估，以根据粒子的分布来估计轮式移动机器人的位姿。这可以通过多种方式实现，例如所有粒子的（加权）平均值或基于粒子的概率。估计位姿如图8.16D所示。

练习。 评估粒子的分布，以确定轮式移动机器人的当前估计。

移动机器人随后再次移动，在下一个时间步，算法进入下一个预测步骤。图8.16E–G 显示了经过三次更多粒子滤波迭代后的估计位姿，而图8.16H 显示了再经过多次迭代后的估计位姿。在演示的案例中，仅当颜色测量值发生变化时才更新粒子滤波器。有关粒子滤波器算法的更多细节，请参见第6.6节。

练习评估粒子滤波器的性能并试验算法参数。在发生机器人劫持（在估计算法暂停时重新定位机器人）以及存在严重车轮打滑的情况下，评估该算法的性能。

练习. 作为一项附加任务，在定位功能正常工作后，实现一个简单的控制算法，使移动机器人能够在环境中自主驾驶前往任意目标。添加额外的传感器以实现对障碍物（场地边界）的检测。

8.5 线路编队中车辆的控制

8.5.1 引言

未来的智能交通系统离不开自主轮式车辆。一个重要应用是在高速公路上实现自动化车队，以所谓的虚拟列车编队自主行驶。车队中的车辆应以所需的最小安全距离精确且安全地跟随其领航车辆。这将提高高速公路的车辆密度，避免交通拥堵，并提高安全性。

在本练习中，将设计一种移动机器人线性编队行驶的控制算法。为了实现自动化的编队行驶，需要精确的传感器系统来测量全局信息（如GPS）或相对信息（如距离和方位角），或两者兼有。在此，我们将实现一种仅依赖相对传感器——激光测距仪(LRF)的分布式控制策略。假设每辆车辆都配备有LRF，用于测量其领航车辆的距离和方位角。该信息随后被用于记录并跟踪领导者车辆的路径。领导者车辆的路径通过跟随者的里程计和激光雷达测量（距离D 和方位角 α）在跟随者的局部坐标系中记录

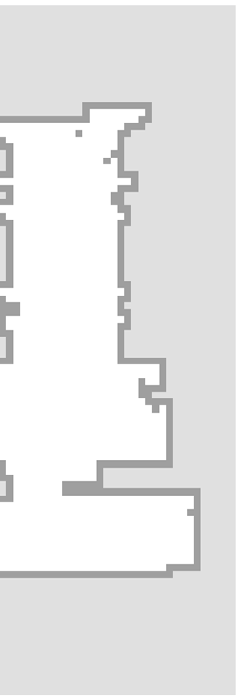
示意图14

如图8.17所示。跟随车辆随后使用第3.3节中介绍的轨迹跟踪控制方法，跟踪其领航车辆的估计路径。众所周知，基于里程计的机器人定位容易受到不同误差的累积（例如车轮打滑、传感器和执行器噪声等）影响，因此仅适用于短期定位。如图所示，在线性编队控制中，使用里程计产生的后续绝对位姿误差并不重要，因为车辆之间关键的是相对位置（D和 α）。该相对位置由激光雷达（LRF）精确测量，而仅使用短期的里程计定位来估计跟随者在未来短时间内需要行驶的领航者路径部分。更多相关信息可参见[3]。

该练习包含三个部分，其中开发的子系统将随后集成到车辆编队控制的实现中。第一部分涉及基于里程计的定位，第二部分描述领航车辆路径估计。在第三部分中，采用轨迹跟踪控制来完成编队控制任务。

8.5.2 基于里程计的定位

里程计是最简单的定位方法，其中通过在机器人已知速度下对机器人运动学模型进行积分来获得位姿估计。如果差分机器人速度在离散时间点发生变化

t= kTS, k= 0, 1, 2,…其中Ts为采样间隔，则下一个机器人位姿（在(k+1)）由当前位姿（k）和当前速度获得（见第2.2.1节）。

x(k+ 1)= x(k)+ v(k)Ts cos(ϕ(k)) y(k+ 1)= y(k)+ v(k)Ts sin(ϕ(k)) ϕ(k+ 1)= ϕ(k)+ω(k)Ts (8.19)

练习。 实现使用里程计的差速驱动机器人的定位，其中机器人初始位姿不重要，因此初始位姿可设为原点。通过将机器人的估计路径与已知的真实路径进行比较来验证定位效果。

8.5.3 估计参考轨迹

已知通过里程计获得的机器人在全局坐标中的当前位姿，机器人还可以根据它们之间的已知相对位置来确定领航机器人的位置。该相对位置由激光雷达测量得到，包含距离D(k) 和到领航机器人的方位角 α(k)。主要思想是记录领航机器人的位置，估计其轨迹，然后跟随机器人可将此轨迹作为参考并跟踪该轨迹。

领航机器人位置（xL(k)，yL(k)， ϕL(k)）按如下方式估计：

xL(k)= x(k)+ D(k) cos(ϕ(k)+ α(k)) yL(k)= y(k)+ D(k) sin(ϕ(k)+ α(k)) (8.20)

如果需要获取领航机器人在某个时间t = kTs 的位置，则使用插值：

xL(t)= xL(kTs)+ t− kTs Ts (xL(k+ 1) Ts − xL(kTs)) yL(t)= yL(kTs)+ t− kTs Ts(yL(k+ 1) Ts − yL(kTs)) (8.21)

练习。 根据已知的跟随车辆位置以及到领航机器人的测量距离和方位角，估计领航车辆的路径。为了验证代码的正确性，可以让领航车辆沿某条路径行驶（手动或通过某个控制器自动控制），然后比较真实路径与估计的机器人路径的形状。注意，由于未知因素，估计的领航机器人坐标原点可能与真实的领航机器人位姿不一致

示意图15 , yref(t0)周围的六个点进行估计。)

（例如，设为零）在基于里程计的定位中跟随者的初始位姿。然而，估计的领导者轨迹的形状必须与真实轨迹相同。

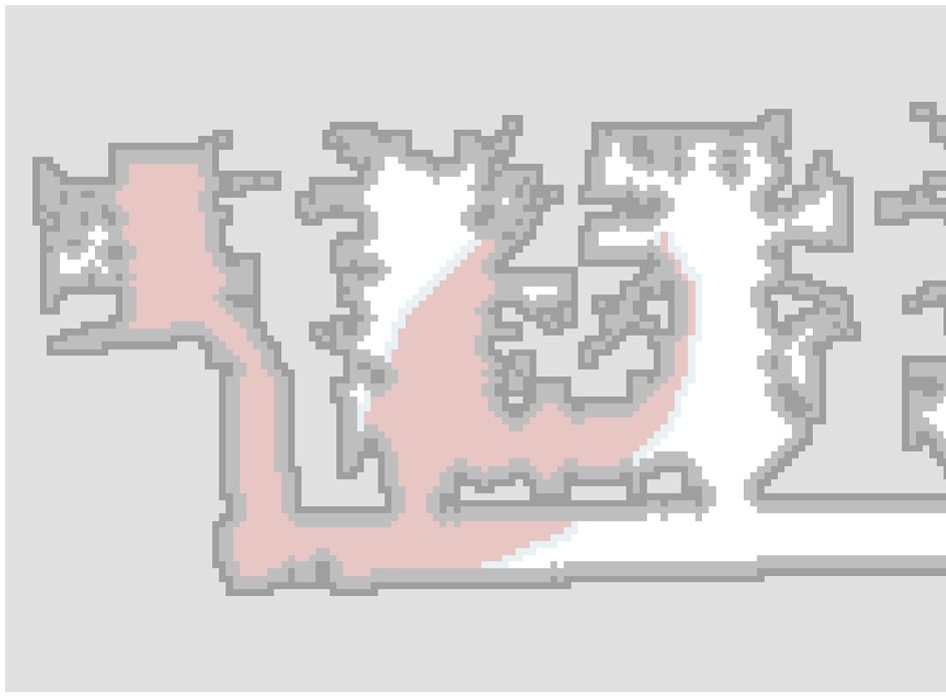
假设每个跟随者必须在领航机器人轨迹上以距离DL进行跟踪。因此在当前时间t0，需要找到领航车辆在时间t= T(xL(T), yL(T)) 的位置，使得该位置与领导者在时间t0和之前位置在t= T之间的距离为DL。该位置即为跟随者的参考（见图8.18）。

练习。 估计跟随机器人的参考位置，使跟随者在路径上落后领导者DL的距离。

为了跟随领导者路径，跟随者不仅需要知道其当前参考位置，还需要了解其参考轨迹。因此，对领导者的估计轨迹 ˆxL(t), ˆyL(t) 采用参数多项式形式进行估计：

xˆL(t)= a2xt2+ a1xt+ a0x yˆL(t)= a2yt2+ a1yt+ a0y (8.22)

选取六个领航机器人位置，参考位置前后各三个，如图8.18所示。多项式axi和ay i(i= 0,1,2)的系数通过最小二乘法计算得出。

后随车辆在当前时间t0 的参考位姿由以下方式确定

⎡⎣ xref(t0) yref(t0) ϕref(t0) ⎤⎦= ⎡⎣ xˆL(T) yˆL(T) ϕˆL(T) ⎤⎦= ⎡⎣ a2x T2+ a1x T+ a0x a2y T2+ a1y T+ a0y atan2(2a2y T+ a1y, 2a2x T+ a1x) ⎤⎦(8.23)

其中atan2(·,·)是反正切的四象限版本（见公式6.43），在Matlab中使用 atan2函数将。参考轨迹估计为时间的二阶多项式函数。使用估计参考位置周围的六个样本，通过最小二乘法识别多项式的参数（公式 8.23）。

8.5.4 线性编队控制

每个跟随车辆需要使用轨迹跟踪控制来跟踪估计的参考轨迹（8.23）。对于轨迹控制器，采用第3.3.6节中定义的非线性控制器，如下所示：

vfb= vref cos eϕ+ kxex ωfb= ωref+ kyvref sin eϕ eϕ ey+ kϕeϕ (8.24)

其中前馈信号（参见第3.3.2节）由式（8.23）定义的估计的参考轨迹得到

vref(t0)= √x˙2ref+ y˙2ref= √(2a2x T+ a1x) 2+(2a2y T+ a1y) 2 (8.25) and

ωref(t0)= x˙ref(t)y¨ref(t)−y˙ref(t)x¨ref(t) x˙2ref(t)+ y˙2ref(t) =(2a2x T+ a1x)2a y x 2 (2a x 2+(2a y 2 (8.26) 控制跟踪误差x(t0), y(t0), ϕ(t0))和其参考位姿(xref(t0), yref(t0), ϕref(t0))计算得到，使用公式(3.35)。

练习。 实现三个机器人的线性编队。第一个机器人可以手动驱动，或自动跟踪某条轨迹。

每个跟随者观察其领导者（例如，机器人2观察机器人1，机器人3 观察机器人2），估计其参考轨迹，并根据控制律（8.24）计算控制动作。在仿真和/或真实机器人上测试车队性能。

8.6 多智能体足球机器人的运动与策略控制

8.6.1 引言

本练习展示了如何对轮式移动机器人进行编程，使其能够自主地参加足球比赛。每个机器人被视作一个智能体，能够感知环境，并具备关于环境、自身目标的知识，以及根据感知信息利用反应式行为采取动作的能力。当多个智能体被应用于实现共同目标（例如进行机器人足球比赛）时，它们需要协作并协调其动作。每个智能体都具备解决基本任务的知识，例如运动、踢球、防守球门等。

练习从在两轮差速驱动移动平台上实现简单的运动控制算法开始，例如轨迹跟踪、到达参考位姿和避障。这些控制算法随后用于编程智能体的不同行为（例如守门员、进攻球员、防守球员）。每种行为都需要考虑当前感知信息，并将该信息映射到动作。例如，守门员需要将自己定位在球门线上以阻挡射门，而进攻球员应具备接近球并将球踢向球门的技能，以及如何避开障碍物（场地边界和其他球员）的能力。行为可以是反应式的，也可以包含某些认知能力，如对球的运动预测，并应相应地规划动作，以更优且更短的时间到达球。

本练习将在图8.19所示的机器人足球实验平台上进行演示，该平台由尺寸为7.5厘米立方体的小型两轮机器人（10个机器人组成2 支队伍）、一个橙色高尔夫球、大小为2.2 × 1.8米的矩形场地、数字彩色相机和个人计算机组成。相机安装在场地上方，用于根据颜色信息跟踪物体（球和球员）[4]。智能体程序的基本操作如图8.19 所示。个人计算机首先为每个智能体分配行为。行为包含定义智能体方向和速度的算法。方向控制器计算机器人的期望平移和角速度，并将其作为

示意图16

通过无线连接向机器人发送参考命令。车载PID控制器实现期望的机器人轮速。请注意，任何其他能够感知自身位置和球的位置的轮式移动机器人也可用于本练习。

该练习包含三个部分，每个部分开发一个子系统，这些子系统是实现完整的多智能体系统所必需的。在第一部分中，编程实现智能体的简单运动能力，以获取球并将其踢入对方球门、防守球门以及避免碰撞。第二部分介绍单个智能体的基于行为的操作。最后一部分引入一个多智能体系统，其中多个智能体在团队中协作，并考虑一种简单的游戏策略。

8.6.2 运动控制

第一个任务需要编写一个运动控制算法，以便从正确的方向接近球并将其推向球门。另一方面，守门员应控制其在球门线前的运动以阻挡进球。

进攻方运动控制

进攻机器人的基本操作是移动到球的位置并将其推向球门。因此，其参考位姿包含参考位置，即球的位置（xref，yref），而参考

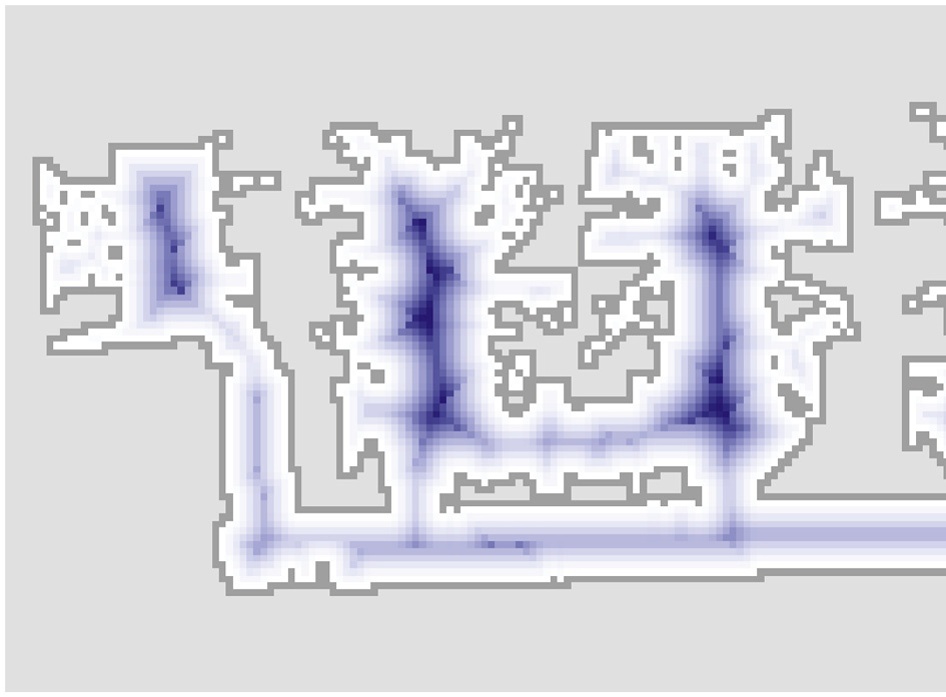
示意图17

姿态(ϕref)是踢球后球的运动的期望方向（见图8.20）。为了击中目标位置(xg, yg)，参考姿态为

ϕref= atan2(yg − yref, xg − xref)

其中atan2(·,·)是反正切的四象限版本（见公式6.43），在 Matlab 中使用atan2函数。

练习。 编写一个控制算法，使机器人能够到达参考位姿。对于控制器实现，可以采用第3.2.3节中描述的基本方法之一。在不同的机器人和球的位置下测试该算法。

控制算法xb、yb）移动时，其性能是否足够？为了移动球，机器人应预测球的未来位置并在该位置拦截。对于非直线机器人运动，通用的预测球位置解难以通过解析方法计算。因此，假设机器人可以沿直线运动，如图8.21所示。根据点积，

[vb cos ϕb, vb sin ϕb] T ·[x − xb, y − yb] T vb√(x − xb) 2+(y − yb) 2 = cos α

角 α被计算出来。然后，使用正弦定理 vbsinβ= v sin α和角 γ= π −α −β表示所需的机器人行驶方向的相对角度 β。最后，从

d sin γ= vbt sinβ可得出机器人到达球所需的时间

t= d sin β vb sin γ (8.27)

示意图18

预测的球位或参考位置是

xref= xb+ vbt cos ϕb yref= yb+ vbt sin ϕb

然而，这种计算出的预测参考位置只有在机器人初始朝向参考位置且期望的踢球方向接近 ϕ时，才能成功用于控制机器人运动。但这种情况很少成立，因为机器人的真实路径通常比计算中假设的直线要长。机器人初始并未朝向预测的参考位置，且最终的踢球方向需要指向球门。如果能够大致估计出机器人到达点xref、yref并具有姿态 ϕref时的真实路径长度l，则可以调整机器人速度，使其在时间t内到达预测的球位，具体如下vn= l t。

练习。 扩展该算法，使机器人不会移向当前球的位置，而是预测其能够到达球的未来球的位置。测试控制算法，并尝试调整参数，以便机器人能够击中移动的球。

直线加速踢球运动控制

如前所述，如果机器人的初始位置朝向球门xg, yg并以加速运动移动，则可以相当准确地将移动的球踢入球门。这种情况如图8.22所示。

未知参考点可根据当前球的位置及其已知运动计算得出：

xref= xb+ vb cos ϕbt yref= yb+ vb sin ϕbt (8.28)

示意图19

或从以下机器人位置，

xref= x+(xg − x)p yref= y+(yg − y)p (8.29)

其中t为机器人以指定直线运动到达球时的时间，p为标量参数。

联立方程（8.28）和（8.29）可得到如下矩阵方程：

[ xg − x −vb cos ϕb yg − y −vb sin ϕb][ p t]=[ xb − x yb − y] (8.30)

其形式为Au= b，其解为u= A−1b。可行解要求 0< p< 1，即拦截球点位于机器人与球门之间。参考点则为

xref= xb+ vbt cos ϕb yref= yb+ vbt sin ϕb

以及考虑其当前速度v后所需的机器人加速度a为

a= 2(√(xref − x)2+(yref − y)2 − vt) t2 (8.31)

练习。 编写一个运动控制算法，使用直线加速运动将移动的球踢入球门。如果存在解，则使用公式(8.31)计算所需的加速度。该计算在

每次控制循环迭代中，新的机器人平移速度设置为v(k)=v(k−1)+ a(k−1)Ts，其中v(k)为当前速度，v(k−1)为先前速度。需要控制角速度，以使机器人沿期望方向 ϕref= arctan yg−y xg−x行驶。测试算法性能。

守门员运动控制

守门机器人运动控制可如下所述。假设机器人在T和T之间的球门线上行驶，如图8.23所示。其当前参考位置xref, yref需要根据球的位置xb, yb及其方向为vb的速度矢量ϕb进行计算，以预测性移动到球将穿过虚线的位置。根据已知数据计算球穿过球门线的时间以及参考位置

t= xg − xb vb cos ϕb xref= xg yref= yb+ vbt sin ϕb ϕref= π 2

其中xg是球门线的坐标。

示意图20

为了驱动机器人沿球门线运动，可使用第3.3.5节中描述的线性轨迹跟踪控制器，其中参考位置的参考速度（vref, ωref）为零。因此控制律简化为

v= kxex ω= kϕeϕ+ sign(v)kyey

其中增益kx、ky和kϕ 可通过实验确定为常数。局部误差ex、ey和 eϕ 使用公式(3.35)计算，且eϕ 必须在范围 −π< eϕ ≤π内。

练习编写一个控制算法，使守门机器人位于球门线（图8.23中的虚线）上以防守球门。通过从不同位置推球朝向球门来测试机器人的性能。观察控制器在存在较大跟踪误差|eϕ| > π 2时的性能；这可以改进吗？

练习。 修改守门员运动控制算法，使其旋转角度不超过 π 2。当 | eϕ| > π 2时，可通过驱动机器人向相反方向运动来实现，并按如下方式修改姿态误差：

eϕ={eϕ −π eϕ> π 2 eϕ+π eϕ< −π 2

避障

如果操场周围有围栏，或者操场上还有其他人员，则机器人的运动控制算法还应考虑避障。实现这种行为的一种方法是使用势场法，类似于第4.2.4节中介绍的方法。

练习。 将其中一个进攻球员控制算法扩展以具备避障能力。

8.6.3 基于行为的智能体操作

假设你有三个机器人在同一支队伍中比赛。第一个机器人是守门员，第二个是进攻球员，第三个是中场球员。对于每个球员或智能体而言，根据比赛中的当前情况（如自身位置、球的位置或其他球员的位置），在其角色（例如守门员）内可能存在不同的行为。在当前时刻，每个智能体都需要决定将执行哪种行为。

这种行为选择可以通过基于反应式行为的架构来实现，这意味着根据当前感知到的环境信息和智能体内部知识，自主地选择最合适的行为。如果有多个可能的行为，则选择优先级更高的那一个。

例如，守门员需要位于球门区内；如果不在球门区内，则需要驶入球门。该到达球门行为可设置为最高优先级。一旦进入球门，守门员就需要防守球门。它需要计算球将从球门线的哪个位置通过，并在球到达之前移动到该位置。如果球并未朝球门方向滚动，守门员可以将自己置于球门线中点位置。

练习. 按照建议为守门员智能体编程至少两种不同的行为。通过手动移动球来验证其性能。

进攻球员智能体在速度过小而无法到达移动的球时，可使用基本运动控制而不进行球预测；否则，可使用预测性运动。如果满足加速直线踢球的条件，则应执行加速直线踢球行为。此外，应检测碰撞的可能性并尝试避免碰撞。但在某些情况下（例如持球时），不应尝试避开其他球员或对手。

练习。 按照建议为进攻球员智能体编程更多不同的行为。通过手动模拟守门员并将球传离球门来验证其性能。

第三名球员是中场球员，这意味着它应尝试移动到操场上的某些（预定义）位置，并朝向对方球门方向。因此，它需要先到达指定位置，若已处于该位置，则需转向球门方向。当前，如果智能体角色为静态，则此智能体看似无用；但如果角色可动态变化（智能体可在比赛中决定成为进攻球员、守门员或中场球员），则其将变得重要，如下一节所述。