啦啦啦,终于又来到了快乐的复习日,这意味着我的生产实习还有一周就要结束了!!!!开心!!!!
今天来复习一下上一周的内容,把昨天没搞的搞一下
复习总结:
本周主要学习了,数组的一些基本知识,帮助更好的去理解shap可视化当中针对回归模型和分类模型不同的shap_value.shape()的维度。
同时学习了如何对基本处理后的模型进行特征工程的方法,针对分类问题的聚类方法,通过聚类生成一个新的特征,但是要注意具体的解读,完成自己的特征工程。
特征工程除了增加,针对高维数据也可以考虑进行特征筛选降维处理,特征降维主要是分为两大类,一部分是只根据特征本身的方差,数据分布等特性进行筛选,还有一部分是针对LDA降维
出来没带当时的学习笔记,比较没有条理,生产实习结束后再进行一个完善补充
(补特昨天常见特征降维的内容
分类用 LDA,可视化用 t-SNE,通用降维 / 去噪用 PCA。
PCA(主成分分析)
定义 :最常用的线性无监督降维方法。 原理 :找到数据中「方差最大」的几个方向(主成分),将高维数据投影到这些方向上,在保留最多信息的同时降低维度。 适用场景 :数据压缩、去除冗余特征、可视化(尤其线性结构数据);例如图像预处理、基因数据降维。
T-SNE(t-分布随机邻域嵌入)
定义 :流行的非线性无监督降维方法。 原理 :通过概率模型,让高维空间中「相似的样本」在低维空间中保持近邻关系,优先保留数据的局部结构。 适用场景 :高维数据可视化(如二维/三维展示);例如单细胞数据、词向量、图像特征的可视化。
LDA(线性判别分析)
定义 :有监督的线性降维方法(需标签数据)。 原理 :找到能「最大化类间差异、最小化类内差异」的投影方向,增强不同类别数据的区分度。 适用场景 :分类任务前的特征降维;例如文本分类、人脸识别等需要提高分类效果的场景。
核心区别
- PCA 无监督,关注全局方差;LDA 有监督,关注类别区分;
- T-SNE 非线性,擅长保留局部结构;PCA/LDA 线性,计算效率更高;
- 可视化首选 T-SNE;分类任务降维首选 LDA;通用数据压缩选 PCA。
PCA降维
# --- 新增:PCA降维处理 ---
print("--- PCA降维处理 --- ")
from sklearn.decomposition import PCA
# 创建PCA实例,降低到10维
pca = PCA(n_components=10, random_state=42)
# 在训练集上拟合PCA并转换数据
X_train_pca = pca.fit_transform(X_train)
# 使用相同的PCA参数转换测试集数据
X_test_pca = pca.transform(X_test)
print(f"原始训练集形状: {X_train.shape}")
print(f"PCA降维后训练集形状: {X_train_pca.shape}")
print(f"原始测试集形状: {X_test.shape}")
print(f"PCA降维后测试集形状: {X_test_pca.shape}")
# 查看解释方差比
print("PCA解释方差比:")
print(pca.explained_variance_ratio_)
print(f"前10个主成分累计解释方差比: {sum(pca.explained_variance_ratio_):.4f}")
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from skopt import BayesSearchCV
from skopt.space import Real, Categorical
import time
import warnings
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score,roc_auc_score# 用于评估分类器性能的指标
from sklearn.metrics import classification_report, confusion_matrix #用于生成分类报告和混淆矩阵
warnings.filterwarnings("ignore")
import umap
# --- 1. 默认参数逻辑回归(基准模型)---
print("--- 1. 默认参数逻辑回归 (训练集 -> 测试集) --- ")
start_time = time.time()
# 初始化模型:默认无正则化(C=1.0)、l2正则化、liblinear优化器
base_model = LogisticRegression(random_state=42)
# 在训练集上拟合模型
base_model.fit(X_train, y_train)
# 在测试集上预测
base_pred = base_model.predict(X_test)
end_time = time.time()
print(f"训练预测耗时: {end_time - start_time:.4f} 秒")
print("默认参数逻辑回归分类报告:")
print(classification_report(y_test, base_pred))
print("默认参数逻辑回归混淆矩阵:")
print(confusion_matrix(y_test, base_pred))
# --- 新增:2. PCA降维后逻辑回归 ---
print("\n--- 2. PCA降维后逻辑回归 (训练集 -> 测试集) --- ")
start_time = time.time()
# 初始化模型
pca_model = LogisticRegression(random_state=42)
# 在PCA降维后的训练集上拟合模型
pca_model.fit(X_train_pca, y_train)
# 在PCA降维后的测试集上预测
pca_pred = pca_model.predict(X_test_pca)
end_time = time.time()
print(f"训练预测耗时: {end_time - start_time:.4f} 秒")
print("PCA降维后逻辑回归分类报告:")
print(classification_report(y_test, pca_pred))
print("PCA降维后逻辑回归混淆矩阵:")
print(confusion_matrix(y_test, pca_pred))
# --- 新增:3. PCA降维效果对比 ---
print("\n--- 3. PCA降维效果对比 --- ")
# 原始特征数量和降维后特征数量
print(f"原始特征数量: {X_train.shape[1]}")
print(f"PCA降维后特征数量: {X_train_pca.shape[1]}")
# 准确率对比
base_accuracy = accuracy_score(y_test, base_pred)
pca_accuracy = accuracy_score(y_test, pca_pred)
print(f"原始数据逻辑回归准确率: {base_accuracy:.4f}")
print(f"PCA降维后逻辑回归准确率: {pca_accuracy:.4f}")
--- PCA降维处理 ---
原始训练集形状: (242, 25)
PCA降维后训练集形状: (242, 10)
原始测试集形状: (61, 25)
PCA降维后测试集形状: (61, 10)
PCA解释方差比:
[0.59157119 0.34804451 0.01434508 0.00856414 0.00677215 0.00609637
0.00546188 0.0034125 0.00299135 0.00230004]
前10个主成分累计解释方差比: 0.9896
--- 1. 默认参数逻辑回归 (训练集 -> 测试集) ---
训练预测耗时: 0.0103 秒
默认参数逻辑回归分类报告:
precision recall f1-score support
0 0.87 0.93 0.90 29
1 0.93 0.88 0.90 32
accuracy 0.90 61
macro avg 0.90 0.90 0.90 61
weighted avg 0.90 0.90 0.90 61
默认参数逻辑回归混淆矩阵:
[[27 2]
[ 4 28]]
--- 2. PCA降维后逻辑回归 (训练集 -> 测试集) ---
训练预测耗时: 0.0046 秒
PCA降维后逻辑回归分类报告:
precision recall f1-score support
0 0.82 0.93 0.87 29
1 0.93 0.81 0.87 32
accuracy 0.87 61
macro avg 0.87 0.87 0.87 61
weighted avg 0.88 0.87 0.87 61
PCA降维后逻辑回归混淆矩阵:
[[27 2]
[ 6 26]]
--- 3. PCA降维效果对比 ---
原始特征数量: 25
PCA降维后特征数量: 10
原始数据逻辑回归准确率: 0.9016
PCA降维后逻辑回归准确率: 0.8689t-SNE
# --- 新增:4. t-SNE降维处理 ---
print("--- t-SNE降维处理 --- ")
from sklearn.manifold import TSNE
# 创建t-SNE实例,降低到2维(t-SNE通常用于可视化,维度不宜过高)
tsne = TSNE(n_components=2, random_state=42, perplexity=30, n_iter=300)
# 在训练集上拟合t-SNE并转换数据
X_train_tsne = tsne.fit_transform(X_train)
# 使用相同的t-SNE参数转换测试集数据
X_test_tsne = tsne.fit_transform(X_test) # t-SNE不支持transform,需要重新拟合
print(f"原始训练集形状: {X_train.shape}")
print(f"t-SNE降维后训练集形状: {X_train_tsne.shape}")
print(f"原始测试集形状: {X_test.shape}")
print(f"t-SNE降维后测试集形状: {X_test_tsne.shape}")
# 可视化t-SNE降维结果
plt.figure(figsize=(10, 8))
plt.scatter(X_train_tsne[:, 0], X_train_tsne[:, 1], c=y_train, cmap='viridis', alpha=0.6)
plt.colorbar(label='类别')
plt.title('t-SNE降维可视化 (训练集)')
plt.xlabel('t-SNE特征1')
plt.ylabel('t-SNE特征2')
plt.tight_layout()
plt.show()
# --- 新增:6. t-SNE降维后逻辑回归 ---
print("\n--- 4. t-SNE降维后逻辑回归 (训练集 -> 测试集) --- ")
start_time = time.time()
# 初始化模型
tsne_model = LogisticRegression(random_state=42)
# 在t-SNE降维后的训练集上拟合模型
tsne_model.fit(X_train_tsne, y_train)
# 在t-SNE降维后的测试集上预测
tsne_pred = tsne_model.predict(X_test_tsne)
end_time = time.time()
print(f"训练预测耗时: {end_time - start_time:.4f} 秒")
print("t-SNE降维后逻辑回归分类报告:")
print(classification_report(y_test, tsne_pred))
print("t-SNE降维后逻辑回归混淆矩阵:")
print(confusion_matrix(y_test, tsne_pred))
--- t-SNE降维处理 ---
原始训练集形状: (242, 25)
t-SNE降维后训练集形状: (242, 2)
原始测试集形状: (61, 25)
t-SNE降维后测试集形状: (61, 2)
--- 4. t-SNE降维后逻辑回归 (训练集 -> 测试集) ---
训练预测耗时: 0.0051 秒
t-SNE降维后逻辑回归分类报告:
precision recall f1-score support
0 0.56 0.17 0.26 29
1 0.54 0.88 0.67 32
accuracy 0.54 61
macro avg 0.55 0.52 0.46 61
weighted avg 0.55 0.54 0.47 61
t-SNE降维后逻辑回归混淆矩阵:
[[ 5 24]
[ 4 28]]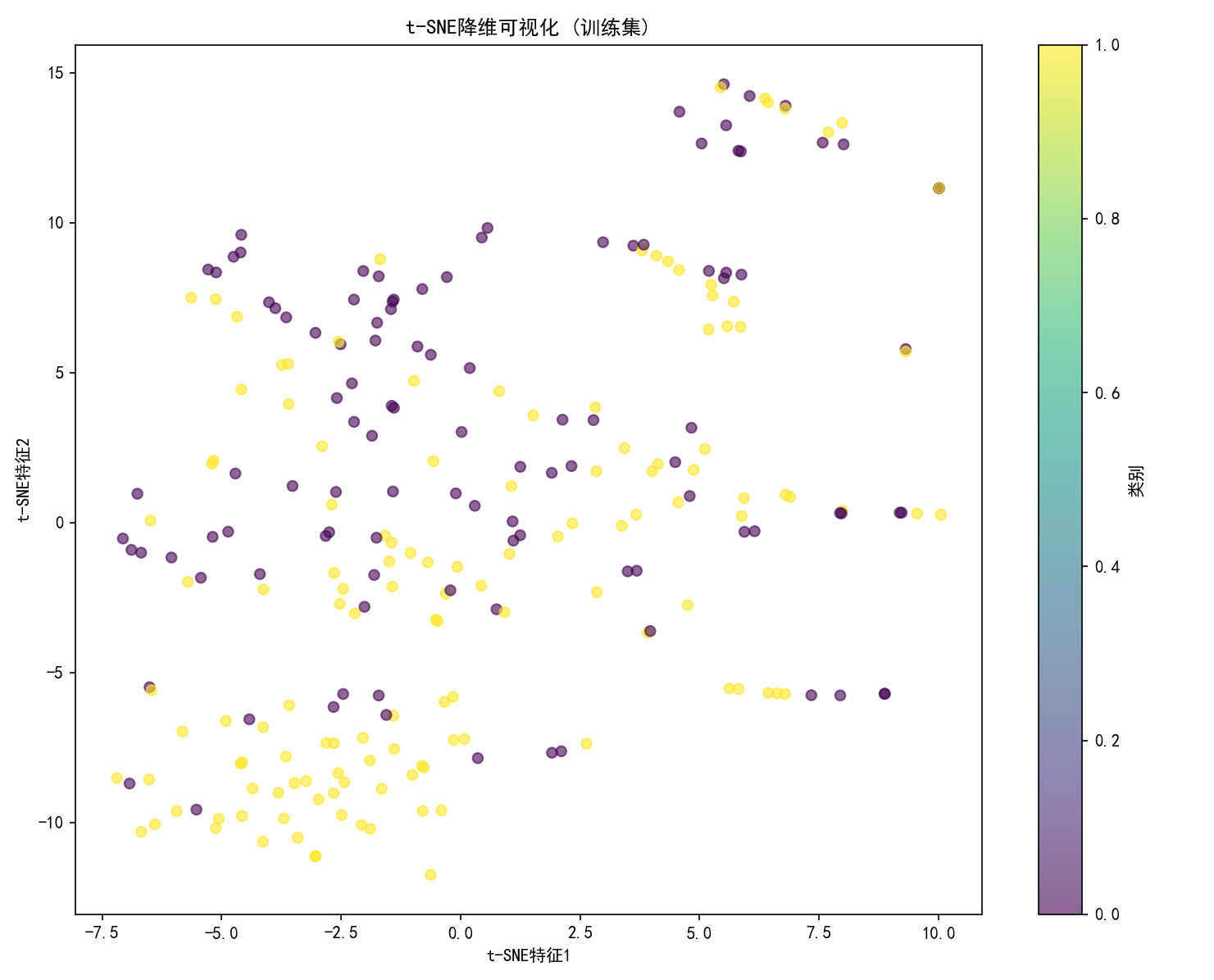
这张图用 t-SNE 展现了训练集高维数据的局部相似性与类别分布,黄 / 紫点的聚集、混合模式,反映了数据在高维空间的复杂关系。若用于分类任务,需注意类别重叠可能带来的模型难点,可进一步结合标签、调整参数或尝试其他降维方法(如 UMAP)对比分析。
LDA
# --- 新增:5. LDA降维处理 ---
print("--- LDA降维处理 --- ")
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 创建LDA实例,降低到1维(二分类问题最多只能降到1维)
lda = LinearDiscriminantAnalysis(n_components=1)
# 在训练集上拟合LDA并转换数据
X_train_lda = lda.fit_transform(X_train, y_train) # LDA需要标签信息
# 使用相同的LDA参数转换测试集数据
X_test_lda = lda.transform(X_test)
print(f"原始训练集形状: {X_train.shape}")
print(f"LDA降维后训练集形状: {X_train_lda.shape}")
print(f"原始测试集形状: {X_test.shape}")
print(f"LDA降维后测试集形状: {X_test_lda.shape}")
# 查看LDA解释方差比
print("LDA解释方差比:")
print(lda.explained_variance_ratio_)
print(f"累计解释方差比: {sum(lda.explained_variance_ratio_):.4f}")
# --- 新增:7. LDA降维后逻辑回归 ---
print("\n--- 5. LDA降维后逻辑回归 (训练集 -> 测试集) --- ")
start_time = time.time()
# 初始化模型
lda_model = LogisticRegression(random_state=42)
# 在LDA降维后的训练集上拟合模型
lda_model.fit(X_train_lda, y_train)
# 在LDA降维后的测试集上预测
lda_pred = lda_model.predict(X_test_lda)
end_time = time.time()
print(f"训练预测耗时: {end_time - start_time:.4f} 秒")
print("LDA降维后逻辑回归分类报告:")
print(classification_report(y_test, lda_pred))
print("LDA降维后逻辑回归混淆矩阵:")
print(confusion_matrix(y_test, lda_pred))
# --- 新增:8. 三种降维方法效果对比 ---
print("\n--- 4. 三种降维方法效果对比 --- ")
# 原始特征数量和各降维方法后的特征数量
print(f"原始特征数量: {X_train.shape[1]}")
print(f"PCA降维后特征数量: {X_train_pca.shape[1]}")
print(f"t-SNE降维后特征数量: {X_train_tsne.shape[1]}")
print(f"LDA降维后特征数量: {X_train_lda.shape[1]}")
# 准确率对比
base_accuracy = accuracy_score(y_test, base_pred)
pca_accuracy = accuracy_score(y_test, pca_pred)
tsne_accuracy = accuracy_score(y_test, tsne_pred)
lda_accuracy = accuracy_score(y_test, lda_pred)
print(f"原始数据逻辑回归准确率: {base_accuracy:.4f}")
print(f"PCA降维后逻辑回归准确率: {pca_accuracy:.4f}")
print(f"t-SNE降维后逻辑回归准确率: {tsne_accuracy:.4f}")
print(f"LDA降维后逻辑回归准确率: {lda_accuracy:.4f}")
# 可视化对比结果
plt.figure(figsize=(12, 6))
methods = ['原始数据', 'PCA降维后', 't-SNE降维后', 'LDA降维后']
accuracies = [base_accuracy, pca_accuracy, tsne_accuracy, lda_accuracy]
plt.bar(methods, accuracies, color=['blue', 'green', 'orange', 'purple'])
plt.title('三种降维方法前后逻辑回归准确率对比')
plt.ylabel('准确率')
plt.ylim(0.7, 1.0)
# 添加准确率数值标签
for i, v in enumerate(accuracies):
plt.text(i, v + 0.01, f'{v:.4f}', ha='center')
plt.tight_layout()
plt.show()--- 5. LDA降维后逻辑回归 (训练集 -> 测试集) ---
训练预测耗时: 0.0048 秒
LDA降维后逻辑回归分类报告:
precision recall f1-score support
0 0.87 0.90 0.88 29
1 0.90 0.88 0.89 32
accuracy 0.89 61
macro avg 0.88 0.89 0.89 61
weighted avg 0.89 0.89 0.89 61
LDA降维后逻辑回归混淆矩阵:
[[26 3]
[ 4 28]]
--- 4. 三种降维方法效果对比 ---
原始特征数量: 25
PCA降维后特征数量: 10
t-SNE降维后特征数量: 2
LDA降维后特征数量: 1
原始数据逻辑回归准确率: 0.9016
PCA降维后逻辑回归准确率: 0.8689
t-SNE降维后逻辑回归准确率: 0.5410
LDA降维后逻辑回归准确率: 0.8852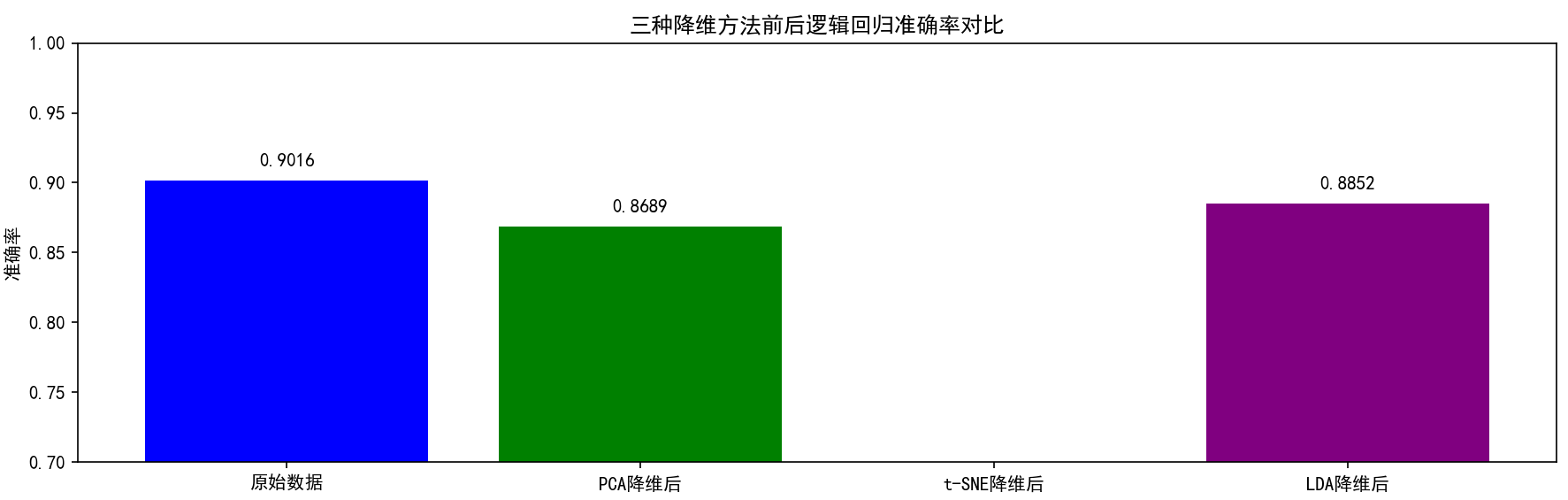





















 796
796

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








