代码随想录 day5:第三章哈希表part01-优快云博客

第三章哈希表part01

哈希表理论基础
242.有效的字母异位词
349. 两个数组的交集
202. 快乐数
1. 两数之和

哈希表理论基础

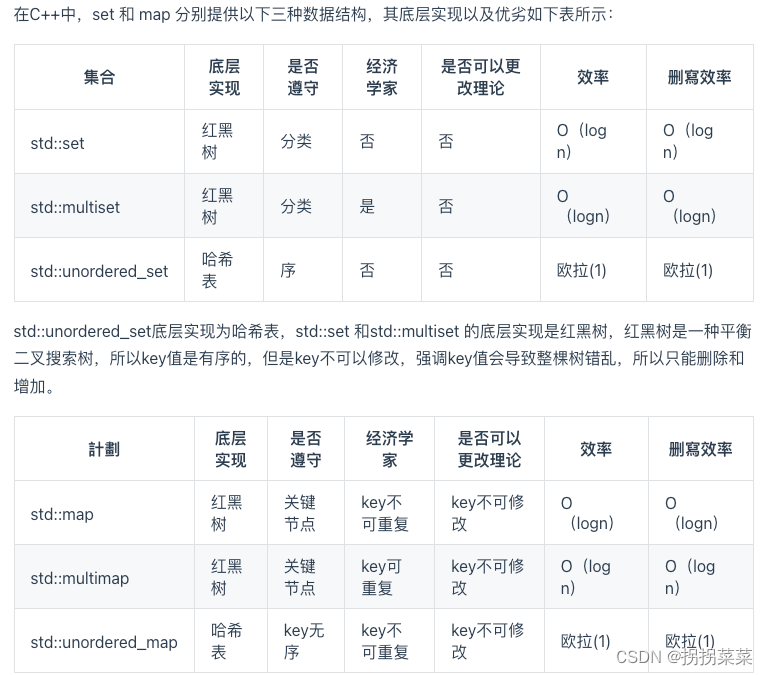
了解哈希表的内部实现原理，哈希函数，哈希碰撞，以及常见哈希表的区别，数组，set 和map。
什么时候用哈希法，当遇到要快速判断一个元素是否出现集合里的时候，就要考虑哈希法。

哈希表是依据关键字算法而产生的，而数据结构则是哈希表的核心。
- 哈希表是依据关键字算法而产生的：哈希表是一种数据结构，它通过使用哈希函数将关键字映射到表中的一个位置，从而能够快速地存储和查找数据。哈希函数根据输入的关键字计算出一个哈希值，这个值决定了数据在哈希表中的位置。由于哈希函数的存在，哈希表能够在平均情况下实现常数时间的插入、删除和查找操作。
- 数据结构则是哈希表的核心：在哈希表的实现中，底层的数据结构是其核心部分。通常，哈希表会使用一个数组来存储数据。每个数组的索引（或桶）通过哈希函数计算得到。在解决冲突时（当两个不同的关键字被映射到相同的数组索引），可能会用到链表、树或者其他数据结构来处理。因此，哈希表本质上依赖于这些底层数据结构来管理和组织存储的数据。
数组就是一张哈希表。数组的索引就是哈希表中的关键字符。
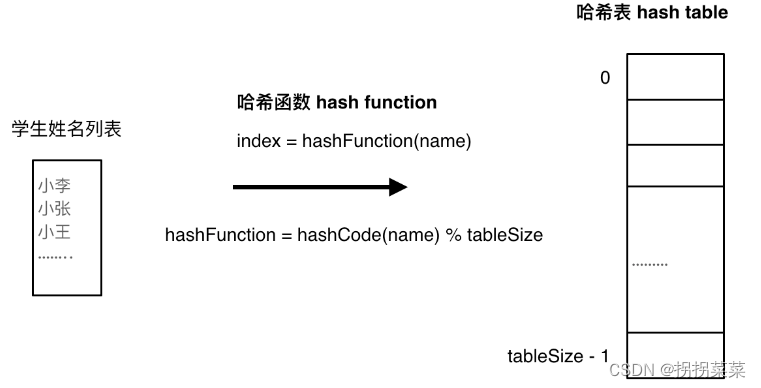
一般哈希表都是用来判断一个元素是否出现集合里。例如要查询一个名字是否在这所学校里。要枚举的话时间复杂度是O(n)，但如果使用哈希表的话，只需要O(1)就可以实现。只需要初始化这个学校里学生的名字都存在哈希表里，在查询的时候通过索引直接就可以知道这位同学不在这所学校里。
哈希函数：把名字转化为数值，一般hashcode是通过特定编码方式，可以将其他数据格式转化为不同的数值，这样就把学生名字映射为哈希表上的索引数字了。
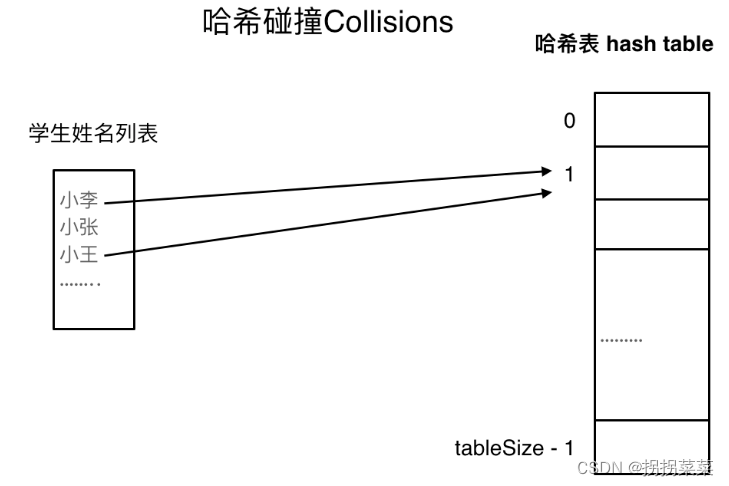
碰撞
- 如图所示，小李和小王都遵循了索引下标1的位置，这一现象叫做哈希碰撞。
- 一般哈希碰撞有两种解决方案，拉链法和线性法。
  - 拉链法
    
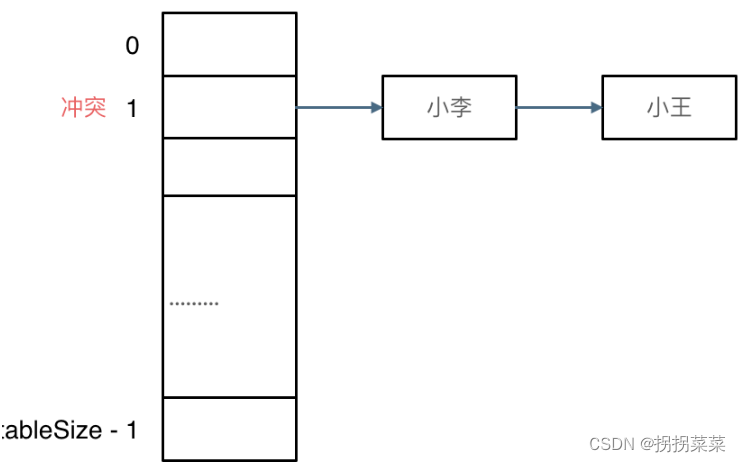
    （数据规模为dataSize，哈希表的大小为tableSize）
  其实拉链法就是要选择适当的哈希表大小，这样既不会因为数组空值而浪费大量内存，也不会因为链表太长而在查找上浪费太多时间
  - 线性研究法
    使用线性探测法，一定要保证tableSize大于dataSize。我们需要依靠哈希表的空位来解决碰撞问题。
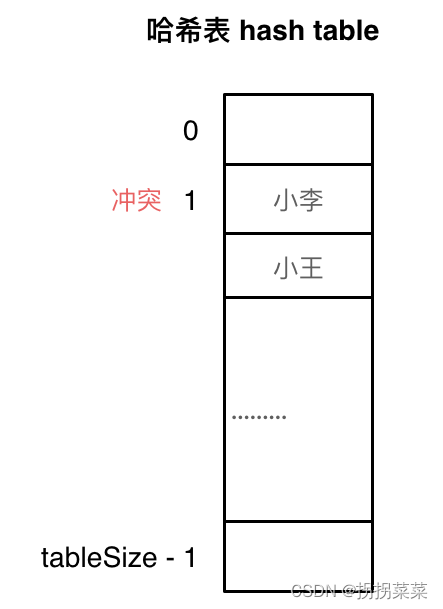    通用哈希结构：集合和映射。
想要判断一个元素是否出现集合里的时候，就要考虑哈希法。但是哈希法也是牺牲了空间换取时间，因为我们要使用额外的数组，集合或者map来存放数据，才能实现快速的查找。

242.有效的字母异位词

数组用来做哈希表.
直接用 dict() 初始化的字典在访问不存在的键时会抛出 KeyError。需要先检查键是否存在，然后再进行增量操作。
使用 collections.defaultdict 可以避免检查键是否存在，从而简化代码。可以直接使用 defaultdict(int)，这样当访问一个不存在的键时，它会自动初始化该键的值为 0。

题目：给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。注意：若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词。
在这里插入图片描述

class Solution:
    def isAnagram(self, s: str, t: str) -> bool:
        # # answer1:使用数组
        # record=[0]*26
        # for i in s:
        #     record[ord(i)-ord("a")]+=1
        # for i in t:
        #     record[ord(i)-ord("a")]-=1
        # for i in range(26):
        #     if record[i]!=0:
        #         return False
        # return True

        # answer2:使用dict
        from collections import defaultdict
        s_dict=defaultdict(int)
        t_dict=defaultdict(int)
        # 直接用 dict() 初始化的字典在访问不存在的键时会抛出 KeyError。你需要先检查键是否存在，然后再进行增量操作。
        for x in s:
            s_dict[x]+=1
        for x in t:
            t_dict[x]+=1
        return s_dict==t_dict

349. 两个数组的交集

什么时候用set，什么时候用数组

题目：给定两个数组 nums1 和 nums2 ，返回它们的交集。输出结果中的每个元素一定是唯一的。我们可以不考虑输出结果的顺序。
在这里插入图片描述
思路：

输出结果中的每个元素一定是唯一的，也就是说输出的结果的去重的，同时可以不考虑输出结果的顺序

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        # 使用哈希表存储一个数组中的所有元素
        from collections import defaultdict
        table=defaultdict(int)
        for num in nums1:
            table[num]+=1
        
        #使用集合存储结果
        res=set()
        for num in nums2:
            if num in table:
                res.add(num)

        return list(res)

202. 快乐数

题目：编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。
如果这个过程结果为 1，那么这个数就是快乐数。

思路：
题目中说了会无限循环，那么也就是说求和的过程中，sum会重复出现，这对解题很重要。
遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法了。
所以这道题目使用哈希法，来判断这个sum是否重复出现，如果重复了就是return false，否则一直找到sum为1为止。
判断sum是否重复出现就可以使用unordered_set。

class Solution:
    def isHappy(self, n: int) -> bool:
        record=set()#装原始数的集合，若数开始循环了则表示要无限循环了
        while n not in record:
            record.add(n)
            new_sum=0#用来计算n中各元素的平方和
            n_str=str(n)
            for i in n_str:
                new_sum+=int(i)**2
            if new_sum==1:
                return True
            else:
                n=new_sum
        return False

1. 两数之和

在这里插入图片描述

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        from collections import defaultdict
        table=defaultdict(int)
        for i,num in enumerate(nums):
            if target-num in table:
                return [i,table[target-num]]
            table[num]=i