卷积神经网络（CNN）自学笔记3：BN层、池化层

原创已于 2024-06-04 21:50:38 修改 · 3.5k 阅读

52 ·

CC 4.0 BY-SA版权

文章标签：

#cnn #笔记 #人工智能

于 2024-06-04 21:48:28 首次发布

部署运行你感兴趣的模型镜像

一、批量归一化层（Batch Normalisation Layer）

1.为什么需要BN层

在深度神经网络训练的过程中，由于网络中参数变化而引起网络中间层数据分布发生变化，这一过程被称为内部协变量偏移（Internal Covariate Shift）。这种分布的变化会使得每一层都需要不断地适应新的输入分布，从而减慢了训练速度，并且可能导致梯度消失或爆炸。

2.BN层定义

BN层通过对每一批数据进行归一化处理，解决了神经网络训练过程中梯度消失和梯度爆炸的问题，加速了训练过程，并且可以在一定程度上减少模型对初始参数的敏感性和对过拟合的依赖。BN层除了能够解决内部协变量偏移问题之外，还提供了一定的正则化效果，从而提高了模型的泛化能力。

总的来说，BN层通过标准化输入特征，解决了训练过程中的内部协变量偏移问题，同时提供了正则化效果，有效提升了模型的训练效率和泛化能力。

3.BN层原理

批归一化的核心思想是在每一层网络的输入上进行标准化处理。具体来说，BN层在每一层网络的每一批数据上做以下操作：

（1）计算批均值和批方差：对于一个批次的数据，我们首先计算每个特征维度的均值和方差：

$\mu =\frac{1}{m}\sum_{i=1}^{m}x_{i}$

$\sigma ^{2}=\frac{1}{m}\sum_{i=1}^{m}\left ( x_{i} -\mu \right )^{2}$

（2）归一化：使用批均值和方差对数据进行标准化处理：

$\hat{x}_{i}=\frac{x_{i}-\mu }{\sqrt{\sigma ^{2}}+\varepsilon }$

其中， $\varepsilon$ 是一个很小的数，防止分母为零。

（3）缩放和平移：引入两个可学习的参数 $\gamma$ 和 $\beta$ ，对标准化后的数据进行缩放和平移：

$y_{i}=\gamma x_{i}+\beta$

其中， $\gamma$ 和 $\beta$ 分别是缩放因子和偏移量，它们的存在允许网络恢复原来的表示能力。

通过上述操作，BN层可以在保持输入数据分布稳定的同时，保留网络的非线性表达能力。

4.在Pytorch中的实现

torch.nn.BatchNorm2d(num_features, 
                     eps=1e-05, 
                     momentum=0.1, 
                     affine=True, 
                     track_running_stats=True, 
                     device=None, 
                     dtype=None)

num_features:输入特征的数量，即卷积层的输出通道数。例如，如果上一层卷积层的输出是[N, C, H, W]，那么num_features应该是C。

eps: 一个小数值，防止分母为零。默认值为1e-5（1*10^-5,0.00001），即公式中的 $\varepsilon$ 。

momentum: 用于计算运行时均值和方差的动量，默认值为0.1。在训练过程中，BN层会计算每个批次的均值和方差，同时也会更新全局的均值和方差。更新公式为：

$running_mean=momentum×batch_mean+(1−momentum)×running_mean$

$running_var=momentum×batch_var+(1−momentum)×running_var$

affine: 若为True，BN层会学习缩放因子和偏移量，分别为 $\gamma$ 和 $\beta$ 。默认值为True。这使得BN层在标准化之后可以进行缩放和平移操作，公式为： $y_{i}=\gamma x_{i}+\beta$

track_running_stats: 若为True，BN层会跟踪全局均值和方差，否则在每个批次上独立计算均值和方差。默认值为True。在训练时，BN层使用批次的均值和方差，而在评估模式下（即model.eval()时），使用全局均值和方差。

在训练和评估模式下，BN层的行为有所不同：

训练模式（model.train()）：
- 使用当前批次的均值和方差进行归一化。
- 更新全局均值和方差。
评估模式（model.eval()）：
- 使用训练过程中累积的全局均值和方差进行归一化。

5.BN层的优缺点

优点：

（1）加速训练：通过稳定输入数据的分布，BN层可以加快模型的训练速度，并允许使用更高的学习率。

（2）减少对初始参数的敏感性：N层减少了模型对初始参数的敏感性，使得训练过程更加稳定。

（3）抑制过拟合：BN层在一定程度上具有正则化效果，有助于抑制过拟合。

缺点：

（1）额外的计算开销：BN层引入了额外的计算操作，增加了训练时间和内存占用。

（2）对小批次不友好：在小批次情况下，计算的均值和方差可能不准确，影响归一化效果。

（3）训练和推理的不一致：在训练和推理阶段，BN层的行为不完全一致，需要特殊处理。

二、池化层（Pooling Layer）

1.池化层定义

通过对特征图进行下采样，减少数据的空间维度，同时保留关键信息，从而降低计算复杂度并减小过拟合风险。

2.池化层的基本原理

池化层的主要作用是通过下采样（downsampling）操作减少特征图的尺寸。池化操作通常在卷积层之后进行，它通过取局部区域内的统计值（如最大值或平均值）来生成缩小后的特征图，从而降低数据的空间维度。

池化层通常有以下几个参数：

（1）池化窗口大小（pool size）：池化操作的窗口大小（如3x3）。

（2）步幅（stride）：池化窗口移动的步长。较大的步幅会导致更多的下采样。

（3）填充（padding）：是否对输入进行填充，以便池化窗口可以完全覆盖输入。

3.常见的池化操作

（1）最大池化（Max Pooling）

最大池化是最常见的池化操作之一。它取池化窗口内的最大值作为该窗口的输出。最大池化可以保留局部区域内最显著的特征，具有良好的平移不变性。

$y_{i,j}=max\left ( x_{i:i+k,j:j+k} \right )$

其中，

$y_{i,j}$ 表示池化输出特征图在位置 (i,j) 的值；

$x$ 表示输入特征图；

$x_{i:i+k,j:j+k}$ 表示输入特征图中以 (i,j) 为左上角、大小为 k×k的池化窗口。

特征图尺寸

torch.nn.MaxPool2d(kernel_size, 
                   stride=None, 
                   padding=0, 
                   dilation=1, 
                   return_indices=False, 
                   ceil_mode=False)

kernel_size ：池化窗口的大小，int或 tuple型

stride：窗口移动步长，默认等于 kernel_size，int, tuple 或 None

padding：在输入特征图的边缘添加的零填充个数，int 或 tuple型，padding=(1, 2) 表示在高度方向添加 1 个零，宽度方向添加 2 个零。

dilation：池化窗口元素之间的间距，int 或 tuple型

（2）平均池化（Average Pooling）

全局平均池化是将整个特征图的所有值取平均，输出一个单一值。它常用于网络的最后一层，替代全连接层，用于减少参数数量和防止过拟合。

$y_{i,j}=\frac{1}{k^{2}}\sum_{p=0}^{k-1}\sum_{q=0}^{k-1}x_{x+p,j+q}$

其中，

$y_{i,j}$ 表示池化输出特征图在位置 (i,j) 的值；

$x$ 表示输入特征图；

$k$ 表示池化窗口的大小，即窗口的宽度和高度；

$x_{x+p,j+q}$ 表示输入特征图中池化窗口内的每个元素；

$\frac{1}{k^{2}}$ 表示归一化因子，用于计算池化窗口内元素的平均值。

特征图尺寸：

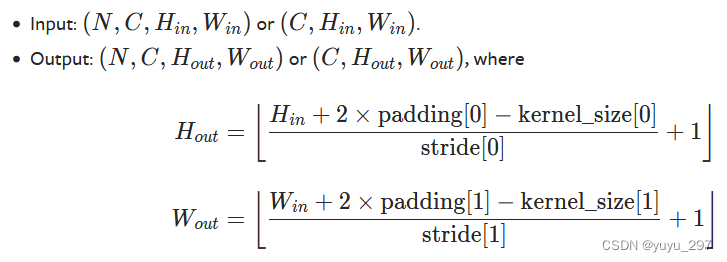
torch.nn.AvgPool2d(kernel_size, 
                   stride=None, 
                   padding=0, 
                   ceil_mode=False, 
                   count_include_pad=True, 
                   divisor_override=None)

各参数的含义同最大池化。

下图展示的是池化窗口大小为2x2，步幅为2的池化操作。

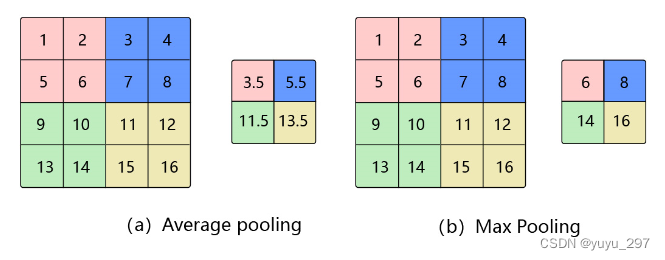
图片转载于：池化 — PaddleEdu documentation

对多通道图像，分别对每个通道做池化操作。

（3）全局平均池化（Global Average Pooling）

全局平均池化没有池化窗口和步幅的概念，而是直接对整个特征图进行操作，通过将每个通道的特征值进行平均，生成一个包含每个通道平均值的一维特征图。它常用于网络的最后一层，替代全连接层，用于减少参数数量和防止过拟合。

对于输入特征图 x 大小为H×W（高度为 H，宽度为W），全局平均池化的计算公式如下：

$y=\frac{1}{H*W}\sum_{i=0}^{H-1}\sum_{j=0}^{W-1}x_{i,j}$

其中，

$y$ 是全局平均池化的输出值；

$H$ 和 $W$ 分别为输入特征的高度和宽度；

$x_{i,j}$ 为特征图中位置为 $\left ( i ,j\right )$ 的值。

同理，全局最大池化。

用法：常用于替换网络最后的flatten和全连接层，减少参数数量。

PyTorch代码实现

torch.nn.AdaptiveAvgPool2d(output_size)

output_size可以是一个元组（H, W），也可以是正方形图像 H x H 的单个 H。H 和 W 可以是一个 int，也可以是 None，即大小与输入相同。

import torch
input = torch.randn(1, 3, 14, 14)
avgpool = torch.nn.AdaptiveAvgPool2d((3,9))
output = avgpool(input)
print(output.size())
# torch.Size([1, 3, 3, 9])

torch.nn.AdaptiveMaxPool2d(output_size, return_indices=False)

import torch
m = torch.nn.AdaptiveMaxPool2d((2,3))
input = torch.randn(1, 64, 8, 9)
output = m(input)
print(output.size())
# torch.Size([1, 64, 2, 3])

图像的目标输出尺寸，形式为 Hout×Wout。可以是一个元组（Hout,Wout），也可以是正方形图像 Hout×Hout 的单个 Hout。Hout 和 Wout 可以是一个 int，也可以是 “None”，这意味着输出大小将与输入大小相同。

最简单的例子：

有一个输入特征图，其形状为 [batch_size, num_channels, height, width]，

使用全局平均池化torch.nn.AdaptiveAvgPool2d((1, 1))后，输出特征图的形状将变为 [batch_size, num_channels]，其中每个通道的值是对应输入特征图在该通道上的平均值。

使用全局平均池化torch.nn.AdaptiveAvgPool2d((2, 1))后，输出特征图的形状将变为 [batch_size, num_channels, 2, 1]。

(4）自适应平均池化（adaptive_avg_pool2d）

torch.nn.functional.adaptive_avg_pool2d(input, output_size)

import torch
input = torch.randn(1, 64, 9, 9)
m = torch.nn.functional.adaptive_avg_pool2d(input, 1)
print(m.size())
# torch.Size([1, 64, 1, 1])

您可能感兴趣的与本文相关的镜像

PyTorch 2.7

PyTorch

Cuda

PyTorch 是一个开源的 Python 机器学习库，基于 Torch 库，底层由 C++ 实现，应用于人工智能领域，如计算机视觉和自然语言处理