决策树算法详解-优快云博客

一、相关概念：

决策树：是一种基于特征对实例进行分类的一种树形结构。它也可以表示为if-else规则的集合，也可以看作是定义在特征空间划分上类的条件概率分布。
熵：①在化学上：代表分子的混乱程度，分子越混乱无序，熵越大；分子越有序，熵越小。
②在信息论与概率统计中：表示随机变量不确定性的度量。随机变量x的熵的定义为：
信息熵：衡量信息有效性的一种度量方法。如果某个信息使我们的判断更加有序、清晰，熵越小，反之越大。
信息增益：表示得知特征x的信息而使得类Y的不确定性减少的程度。定义公式：
经验熵：当熵中的条件概率由数据估计（特别是极大似然估计）得到时，熵就对应经验熵。
经验条件熵：当熵中的条件概率由数据估计（特别是极大似然估计）得到时，条件熵就对应经验条件熵。
条件概率：表示一个子空间上的概率。如果一个事件发生在R空间上，那么[-6, 6]的子空间就是该事件的条件概率。
基尼指数：直观上说，就是从样本数据集D中选取两个样本点，这两个样本点的类别不一致的概率。
公式可定义为：分类问题中，数据集有K个类，其中样本点属于第k个类的概率为 $p_{k}$ ，则概率分布的基尼指数为：
$Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kpk2.Gini(p)=\sum_{k=1}^{K}p_{k}(1-p_{k})=1-\sum_{k=1}^{K}p_{k}^2.$
对于二分类问题，假设第一个样本点属于第1个类的概率为 $p$ ，则二分类问题的概率分布为：
$G i n i (p) = 2 * p (1 - p) .$
对于给定的样本数据集D，
$Gini(D)=1−∑k=1K(∣Ck∣∣D∣)2.Gini(D)=1-\sum_{k=1}^{K}( \frac{\left | C_{k} \right |}{\left | D \right |})^2.$
其中，K是类别的数目， $C_{k}$ 表示属于第k类的样本子集。

二、决策树综述：

决策树旨在学习一个与训练数据集拟合程度很好，但模型复杂度又小的模型。
决策树算法由三部分构成：特征选择、决策树的生成、决策树的剪枝。
决策树常见的算法有：ID3、C4.5、CART。

三、特征选择：

特征选择：
特征选择的目的在于选取对训练数据集能够分类的特征，而特征选择的关键是特征选择准则。
特征选择准则：
①信息增益：（样本集合D对特征A的的信息增益（ID3））
$g (D, A) = H (D) - H (D ∣ A)$
$H(D)=−∑k=1K∣Ck∣∣D∣log2∣Ck∣∣D∣H(D)=-\sum_{k=1}^{K}\frac{\left | C_{k} \right |}{\left | D \right |}log_2\frac{\left | C_{k} \right |}{\left | D \right |}$
$H(Di)H(D|A)=\sum_{i=1}^{n}\frac{\left | D_{i} \right |}{\left | D \right |}\: H(D_{i})$
②信息增益比：（样本集合D对特征A的的信息增益（C4.5））
$gR(D,A)=g(D,A)HA(D)g_R(D,A)=\frac{g(D,A)}{H_A(D)}$
③基尼指数：（样本集合D的基尼指数（CART））
$Gini(D)=1−∑k=1K(∣Ck∣∣D∣)2.Gini(D)=1-\sum_{k=1}^{K}( \frac{\left | C_{k} \right |}{\left | D \right |})^2.$
样本集合D对特征A的基尼指数：
$Gini(D,A)=∣D1∣∣D∣Gini(D1)+∣D2∣∣D∣Gini(D2)Gini(D,A)=\frac{\left | D_{1} \right |}{\left | D \right |}Gini(D_{1})+\frac{\left | D_{2} \right |}{\left | D \right |}Gini(D_{2})$

四、决策树的生成：

ID3 生成算法：
C4.5生成算法：
CART生成算法：

五、决策树的剪枝：

主要分为预剪枝和后剪枝两种策略。

ID3算法和C4.5算法的剪枝算法：
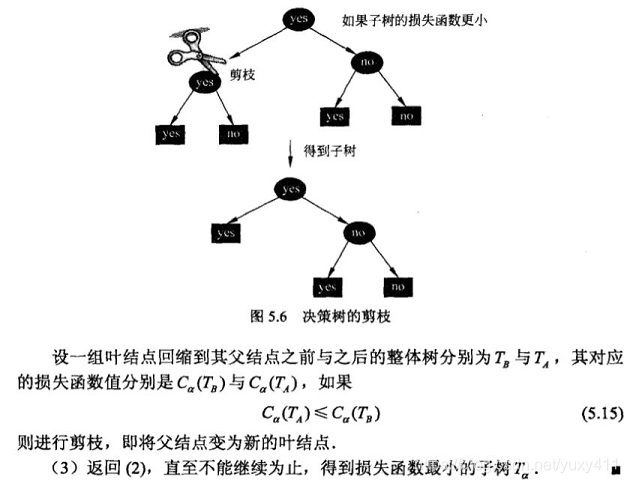
CART算法的剪枝算法

六、疑问：

为什么ID3算法要以信息增益为选择最优特征的选择准则？而不选择经验条件熵？
经验条件熵 H(D|A)表示特征A加入之后，集合D的不确定性。
而信息增益=H(D)-H(D|A)，表示因为特征A的原因，导致集合D的不确定性减少的程度。
所以，信息增益代表的是一种变化差，更有说服力。
为什么C4.5算法使用信息增益比作为选择最优属性的准则，而不是选择信息增益？
因为信息增益具有一个缺点，总是对取值较多的属性具有偏好，例如经典的确定某个西瓜是好瓜还是坏瓜，以编号为特征其信息增益大于纹理特征（最优特征），但是不能选择编号作为划分特征。
而信息增益比需要在信息增益的前提下，除一个特征的固有属性。但是以信息增益比为选择最优划分特征时，又会出现选择属性取值较少的特征偏好，所以C4.5算法采用启发式策略，通过选择信息增益高于平均水平的特征，再从中选择信息增益比较高的特征。

Reference：《统计学习方法》——李航