前言
一般来说想让电机从A点运动到B点,这个过程需要规划轨迹,也就是要指明每一个控制器的伺服周期内电机需要到达的位置点。
为什么要生成每个伺服周期的位置点呢?直接设置起点和终点不行吗?如果直接设置A点和B点,也就是让电机在一个伺服周期内运动到B点,这个距离可能比较长,那么这个伺服周期的误差非常大,这让控制器在这个伺服周期内给很大的电流,从而对电机造成冲击。
那在A点到B点之间根据伺服周期等间隔生成位置点不行吗?可以,这等于规划了A点到B点的速度,但默认加速度是跳变,速度可以瞬间(一个伺服周期内)达到,这相当于一阶轨迹规划
那么不同阶数的轨迹规划有什么分别呢?
二阶与三阶轨迹规划对比
轨迹规划的最大作用就是产生一段平滑的运动曲线。平滑的轨迹规划可以降低系统振动,提高系统运行寿命,同时将输入信号主要集中低频段也有利于系统追踪输入信号。
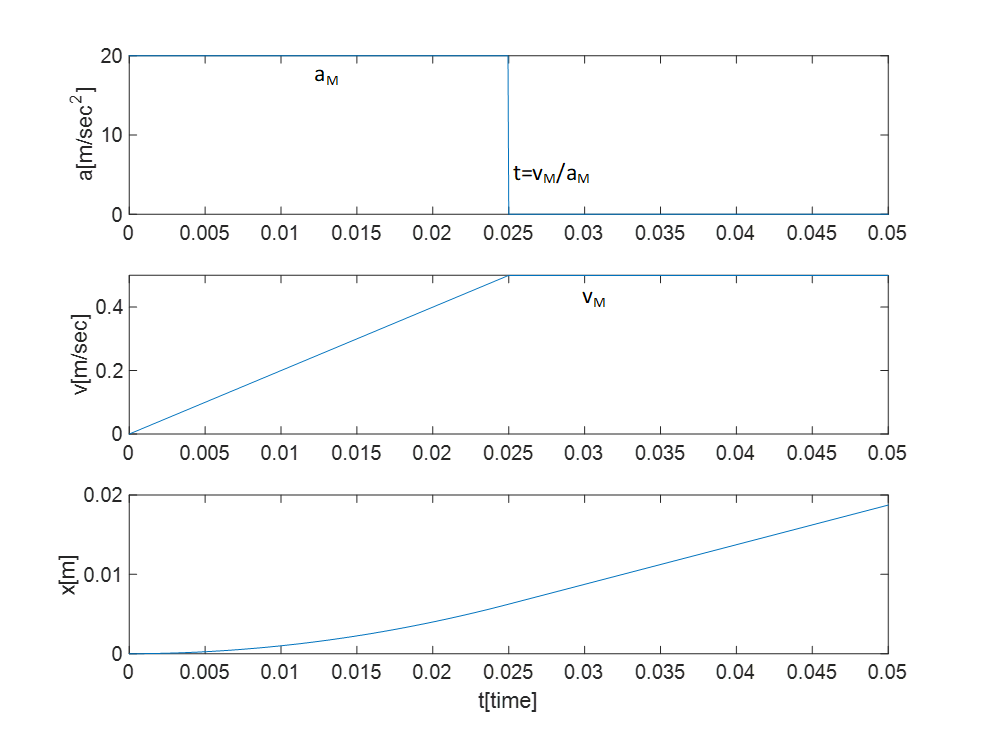
二阶轨迹规划如下图所示:
对二阶轨迹规划的加速度曲线做FFT结果如下:
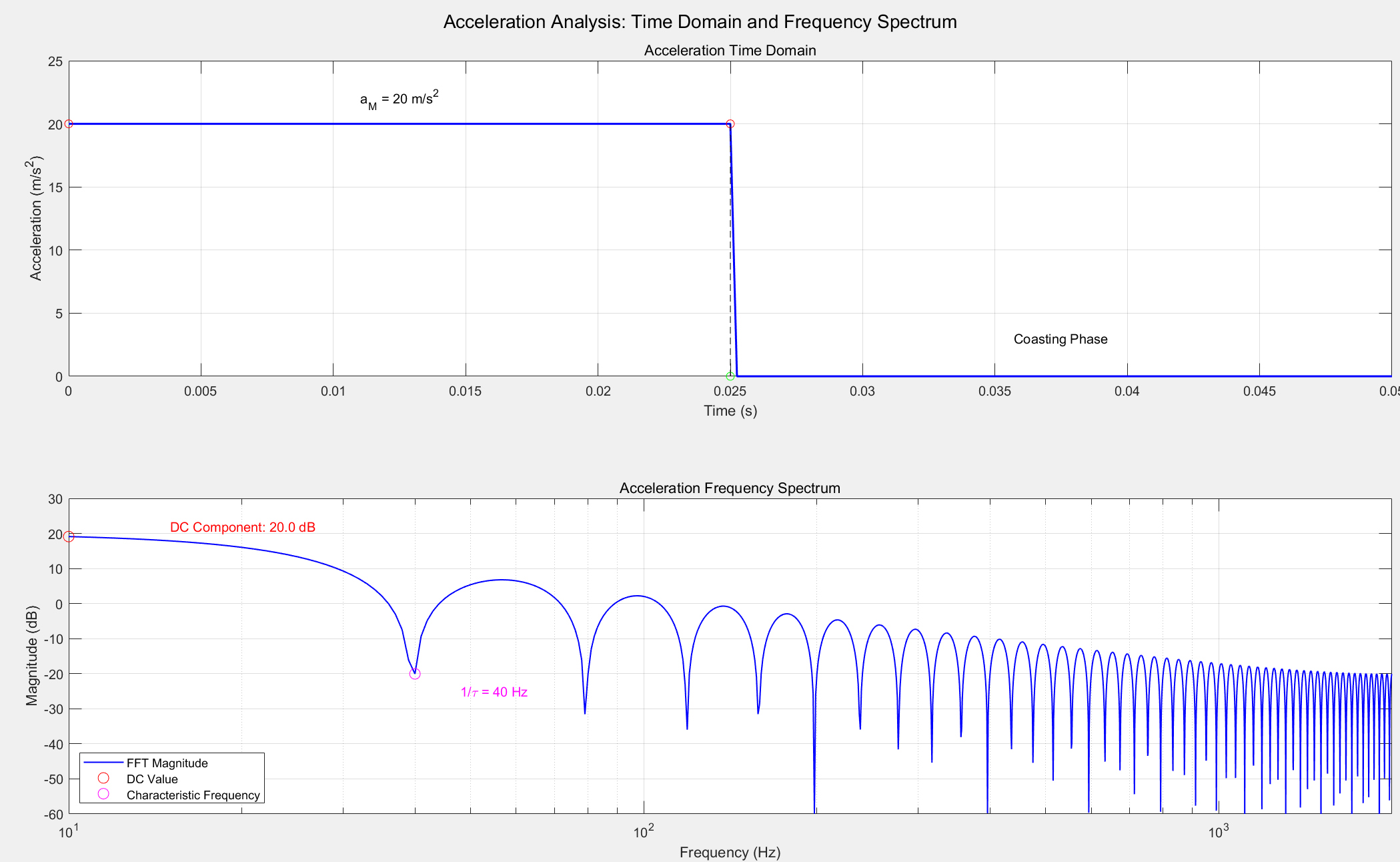
从FFT曲线上分析:凹陷位置点是a/v = 20 / 0.5 = 40Hz的倍频,即频率依次是40Hz,80Hz,120Hz......
附录脚本(AI):
%% 参数设置
fs = 4000; % 采样频率4000Hz(满足Nyquist定理)
t_total = 0.05; % 总时长0.05秒
t = 0:1/fs:t_total; % 时间向量(201个点)
a_M = 20; % 峰值加速度值
%% 创建加速度信号(根据图像描述)
% 0~0.025s: 20 m/s², 0.025~0.05s: 0 m/s²
x = a_M * (t <= 0.025); % 逻辑索引创建信号
%% 绘制时域曲线
figure;
subplot(2,1,1); % 创建上半部分用于时域图
plot(t, x, 'b', 'LineWidth', 1.5);
xlabel('Time (s)');
ylabel('Acceleration (m/s^2)');
title('Acceleration Time Domain');
xlim([0, 0.05]);
ylim([0, 25]);
grid on;
% 添加关键点标记
hold on;
plot([0, 0.025], [20, 20], 'ro', 'MarkerSize', 6); % 起点标记
plot(0.025, 20, 'ro', 'MarkerSize', 6); % 转折点
plot(0.025, 0, 'go', 'MarkerSize', 6); % 零点开始
text(0.0125, 22, 'a_M = 20 m/s^2', 'HorizontalAlignment', 'center');
text(0.0375, 3, 'Coasting Phase', 'HorizontalAlignment', 'center');
line([0.025, 0.025], [0, 20], 'Color', 'k', 'LineStyle', '--'); % 垂直线
%% FFT分析
% 补零到4000点(提高频谱分辨率)
N = 4000; % FFT点数
x_padded = [x, zeros(1, N - length(t))]; % 补零操作
% FFT计算
X = fft(x_padded); % FFT变换
X_mag = abs(X)/length(x); % 幅度归一化(除以原信号长度)
X_dB = 20*log10(X_mag + eps); % dB单位(加eps避免log10(0)错误)
% 频率轴生成(单边谱)
f = (0:N-1)*(fs/N); % 完整频率轴
valid_idx = f <= fs/2; % 有效频率索引(0~2000Hz)
valid_f = f(valid_idx);
X_dB_valid = X_dB(valid_idx); % 对应的有效频域数据
%% 绘制FFT图(10倍频程)
subplot(2,1,2); % 创建下半部分用于频域图
semilogx(valid_f, X_dB_valid, 'b', 'LineWidth', 1);
xlabel('Frequency (Hz)');
ylabel('Magnitude (dB)');
title('Acceleration Frequency Spectrum');
grid on;
% 坐标范围设置
xlim([10, 2000]); % 扩展到2000Hz(Nyquist频率)
ylim([-60, 30]); % 适当调整纵轴范围
%% 添加关键频率标记
% 计算理论直流分量(平均值)
dc_value = a_M * (0.025 - 0) / (0.05 - 0); % 面积/总时长 = 10 m/s²
ideal_dB = 20*log10(dc_value); % ≈20 dB
% 标记直流分量
hold on;
semilogx(10, X_dB_valid(find(valid_f >= 10, 1)), 'ro', 'MarkerSize', 8);
text(15, ideal_dB+2, sprintf('DC Component: %.1f dB', ideal_dB), 'Color', 'r');
% 标记特征频率(1/脉冲宽度)
pulse_width = 0.025;
characteristic_freq = 1/pulse_width; % 40 Hz
[~, idx] = min(abs(valid_f - characteristic_freq));
semilogx(valid_f(idx), X_dB_valid(idx), 'mo', 'MarkerSize', 8);
text(characteristic_freq*1.2, X_dB_valid(idx)-5,...
sprintf('1/\\tau = %.0f Hz', characteristic_freq), 'Color', 'm');
legend('FFT Magnitude', 'DC Value', 'Characteristic Frequency', 'Location', 'southwest');
%% 设置统一标题
sgtitle('Acceleration Analysis: Time Domain and Frequency Spectrum', 'FontSize', 14);
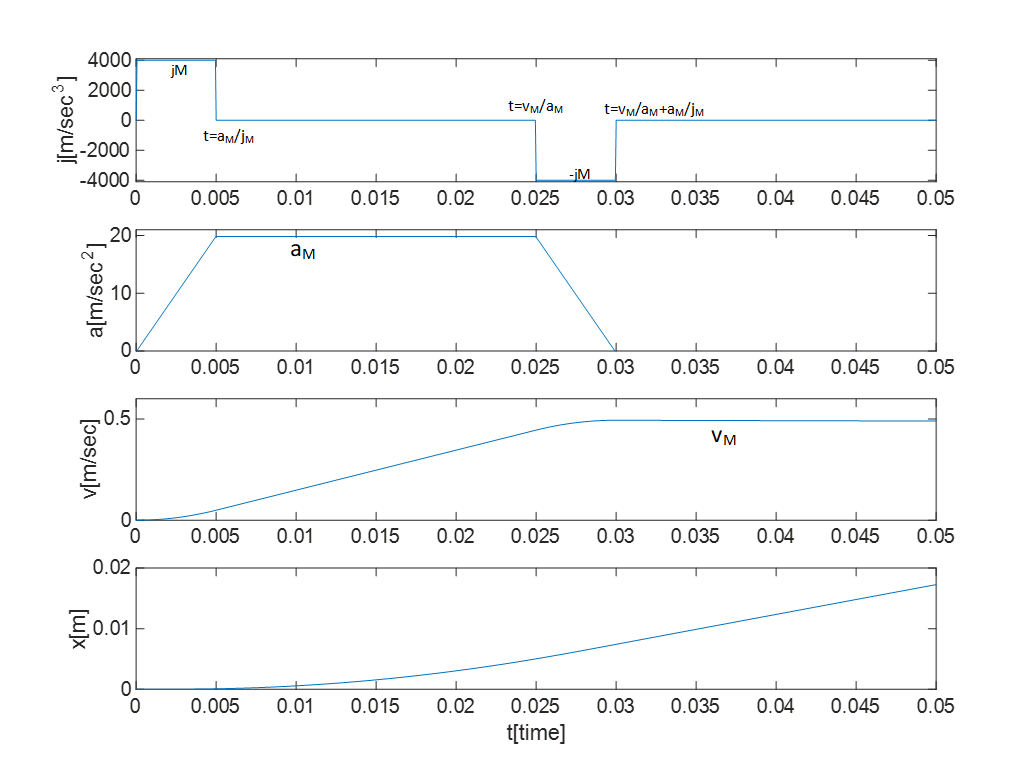
三阶轨迹规划如下图所示:
将二阶和三阶的轨迹规划的FFT做对比如下图
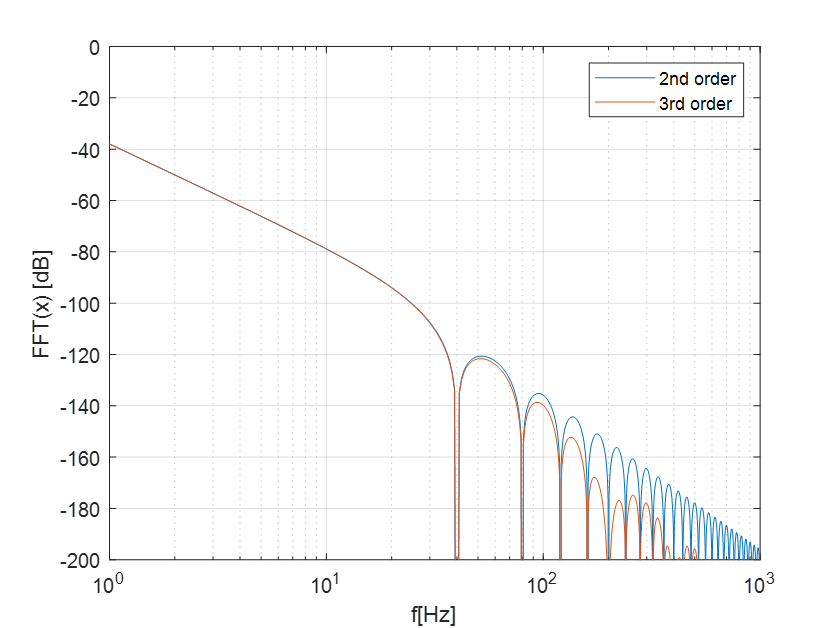
容易看出三阶轨迹规划的高频分量低于二阶轨迹规划的高频分量。
Tips:从上面的对比可以看出规划轨迹越平滑(阶级越高),其信号的高频分量就越少,常见系统都是对低频分量追踪效果很好而对高频信号追踪很差(闭环带宽定义),所以输入信号的越集中于低频,系统对输入信号的追踪效果越好,也就是误差更低,响应更快。
轨迹规划的阶数越高其性能表现的越好,但同时对硬件资源的要求也越高,一般来说三阶和四阶轨迹规划已基本能满足工业高精度控制的需求。
不同速度对跟随误差的影响
用constant与积分模块模拟不同速度输入命令,输入给相同的系统传函(PI控制器+plant),观察error的变化。仿真图如下所示:
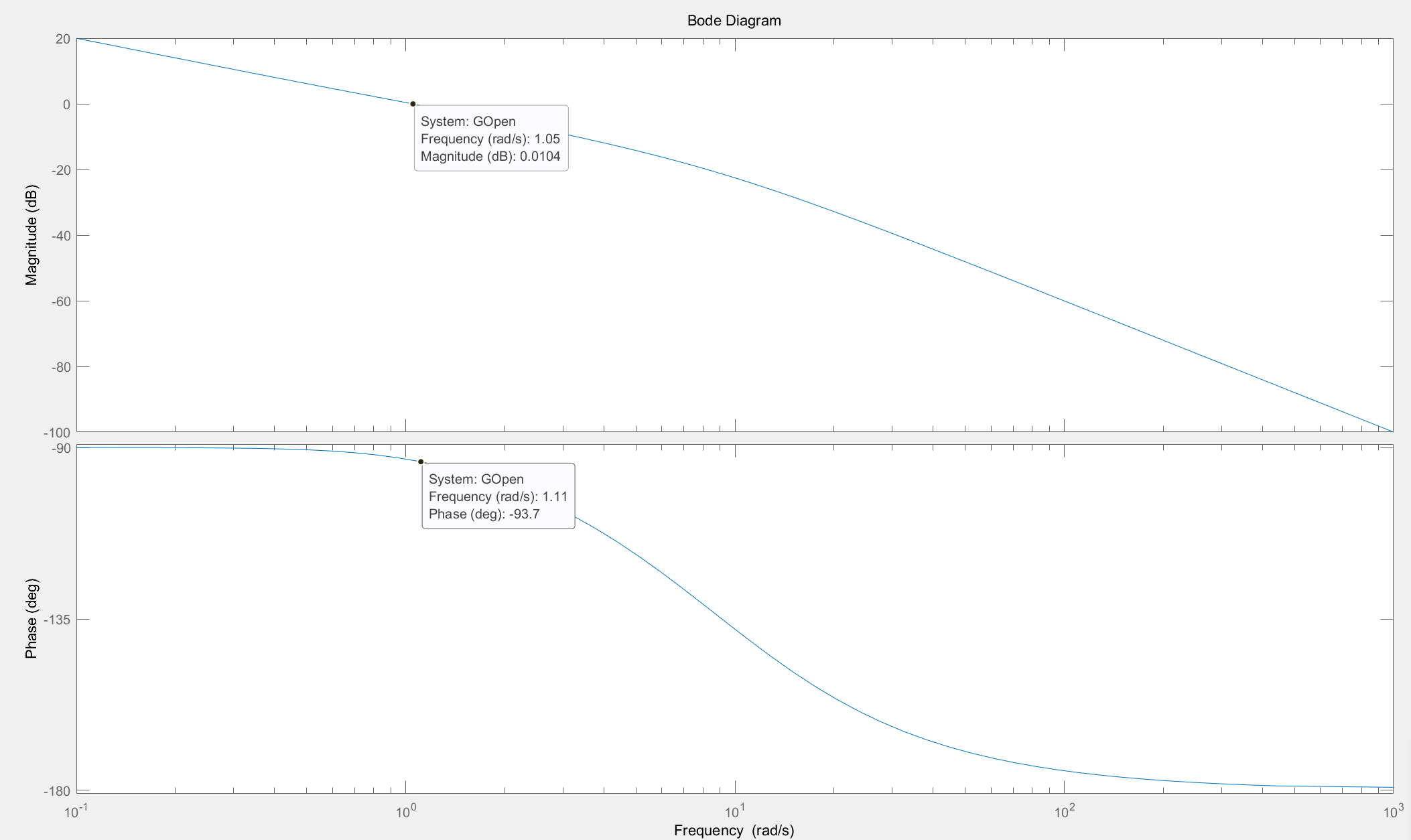
其中仿真的系统传函伯德图如下所示,系统带宽越1rad/s左右。
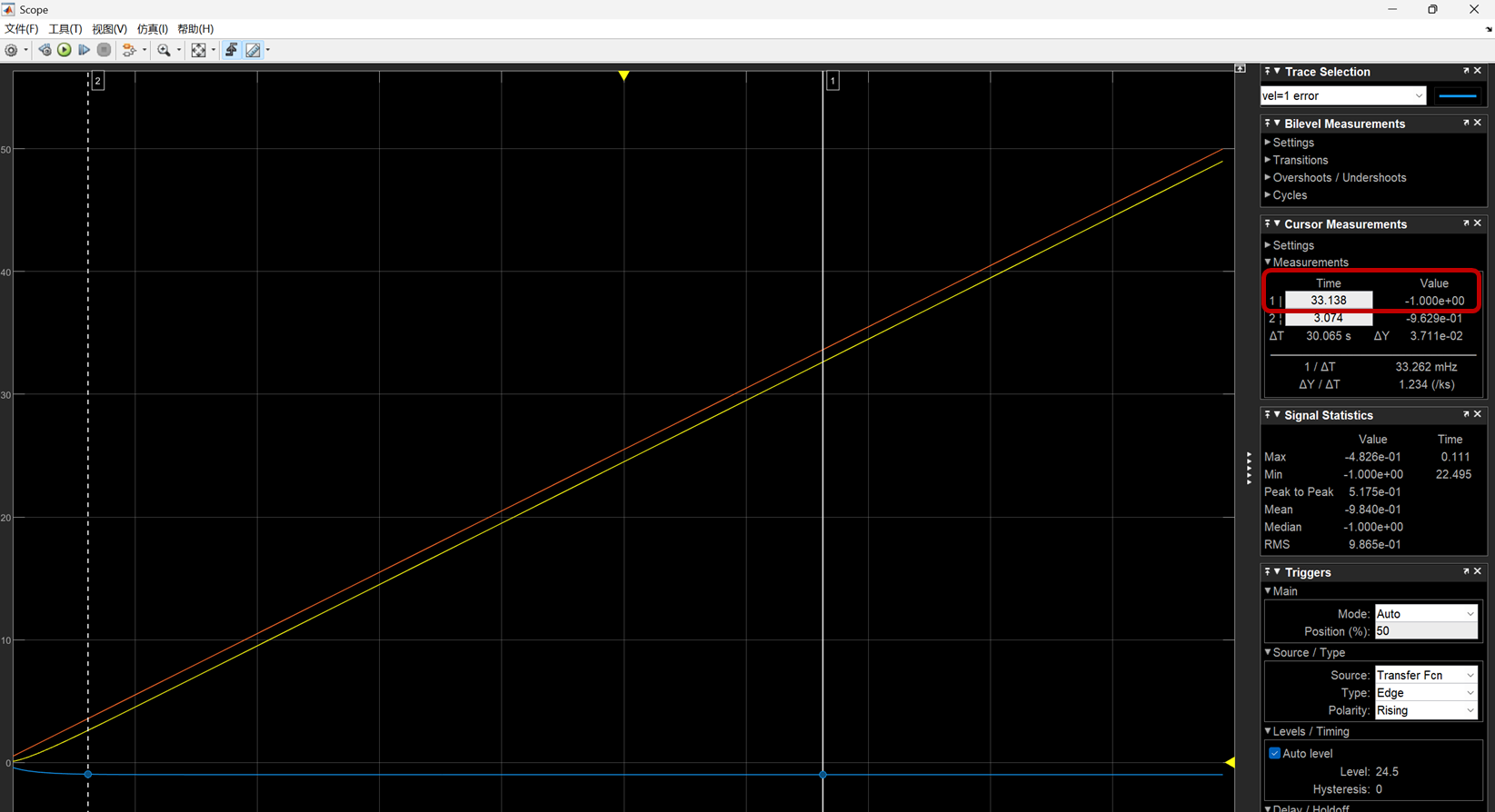
速度输入为1时结果如下,其中红色线条为输入命令,黄色为输出,蓝色线为速度 =1 时的error,error = 输出 - 输入;最终误差稳定在1
速度输入为10时结果如下,其中红色线条为输入命令,黄色为输出,蓝色线为速度 =10 时的error,error = 输出 - 输入;最终误差稳定在10
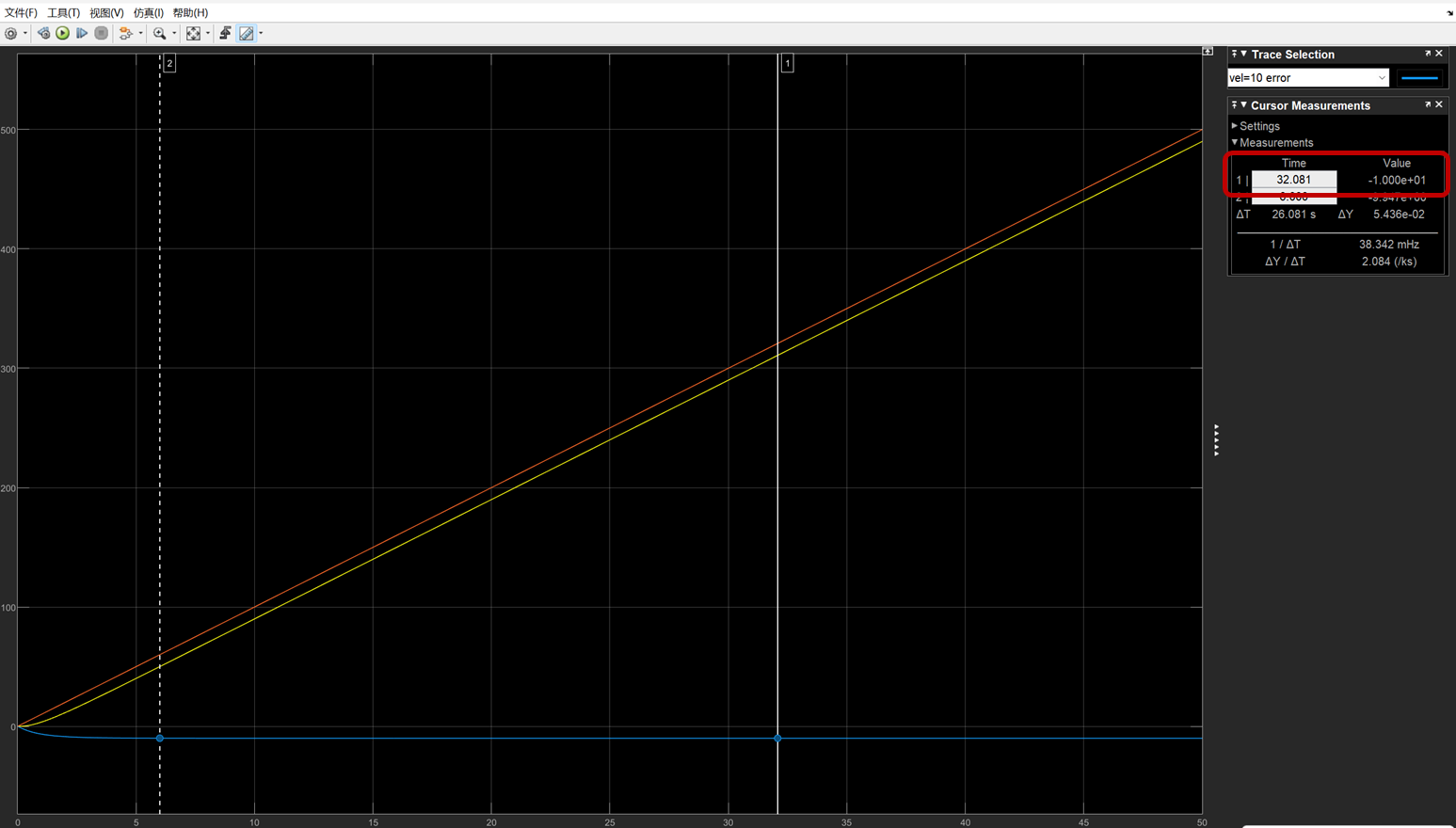
从上述结果上可以看出,对于相同的control + plant ,速度越快跟随误差越大,且误差与速度成正比。




















 523
523

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








