小样本学习记录————用于深度网络快速适应的模型不可知元学习(MAML)

相关概念

小样本学习（Few-Shot Learning）

Few-Shot Learning(FSL) is a type of machine learning problems (specified by E, T and P), where E contains only a limited number of examples with supervised information for the target T.

简单来说就是使用少量样本数据进行训练完成目标任务的一种机器学习方法。具体有关小样本学习的介绍可以看我的上一篇博客https://blog.youkuaiyun.com/yunlong_G/article/details/121570804

N-way K-shot

这是小样本学习中常用的数据，用以描述一个任务：它包含N个分类，每个分类只有K张图片。K越小，N越大越难实现。

Support set and Query set

Support set指的是参考集，Query set指的是查询集。其实就是训练集和测试集。

eg:

用人识别动物种类，有5种不同的动物，每种动物2张图片，总计10张图片给人做参考。另外给出5张动物图片，让人去判断各自属于那一种类。那么10张作为参考的图片就称为Support set，5张要分类的图片就称为Query set。这可以说是一个5-way-2-shot的任务。

元学习（Meta-Learning）

Meta-learning, also known as“learning to learn”, refers to improving the learning ability of a model through multiple training episodes so that it can learn new tasks or adapt to new environments quickly with a few training examples.

元学习又称“学会学习”，是指通过多次训练来提高模型的学习能力，使其能够通过几个训练实例快速学习新任务或适应新环境。现有的方法主要分为两类：

• (1)基于优化的方法，包括开发一个元学习器作为优化器，直接为每个学习者输出搜索步骤，以及学习模型参数的优化初始化，这些参数稍后可以通过几个梯度下降步骤来适应新任务
• (2)基于度量的方法，包括Matching Network、PROTO、Relation Network、TapNet和Induction Network，旨在学习适当的距离度量，以将验证点与训练点进行比较，并通过匹配训练点进行预测。

现在小样本学习的主流方法主要是基于元学习或者迁移学习的，而MAML是元学习中特别经典的一篇论文，所以在此将自己的阅读收获分享给大家。

MAML思想

算法目标： 是一个模型可以经过比较少的训练快速迭代到最好的效果。

为了达到这一目的，模型需要大量的先验知识来不停修正初始化参数，使其能够适应不同种类的数据。这里需要借助李宏毅老师课堂的PPT图来理解一下MAML和预训练的区别。

---

我们定义初始化参数为 $\varphi$，其初始化参数为 ${\varphi }_0$ ，定义在第n个测试任务上训练之后的模型参数为 ${\hat{\theta }}^n$ ，于是总的损失函数为 $L(\varphi )={\sum }_{n=1}^N{l}^n({\hat{\theta }}^n)$ 。pre-training的损失函数是$L(\varphi )={\sum }_{n=1}^N{l}^n(\varphi )$，直观上理解是MAML所评测的损失是在任务训练之后的测试loss，而pre-training是直接在原有基础上求损失没有经过训练。

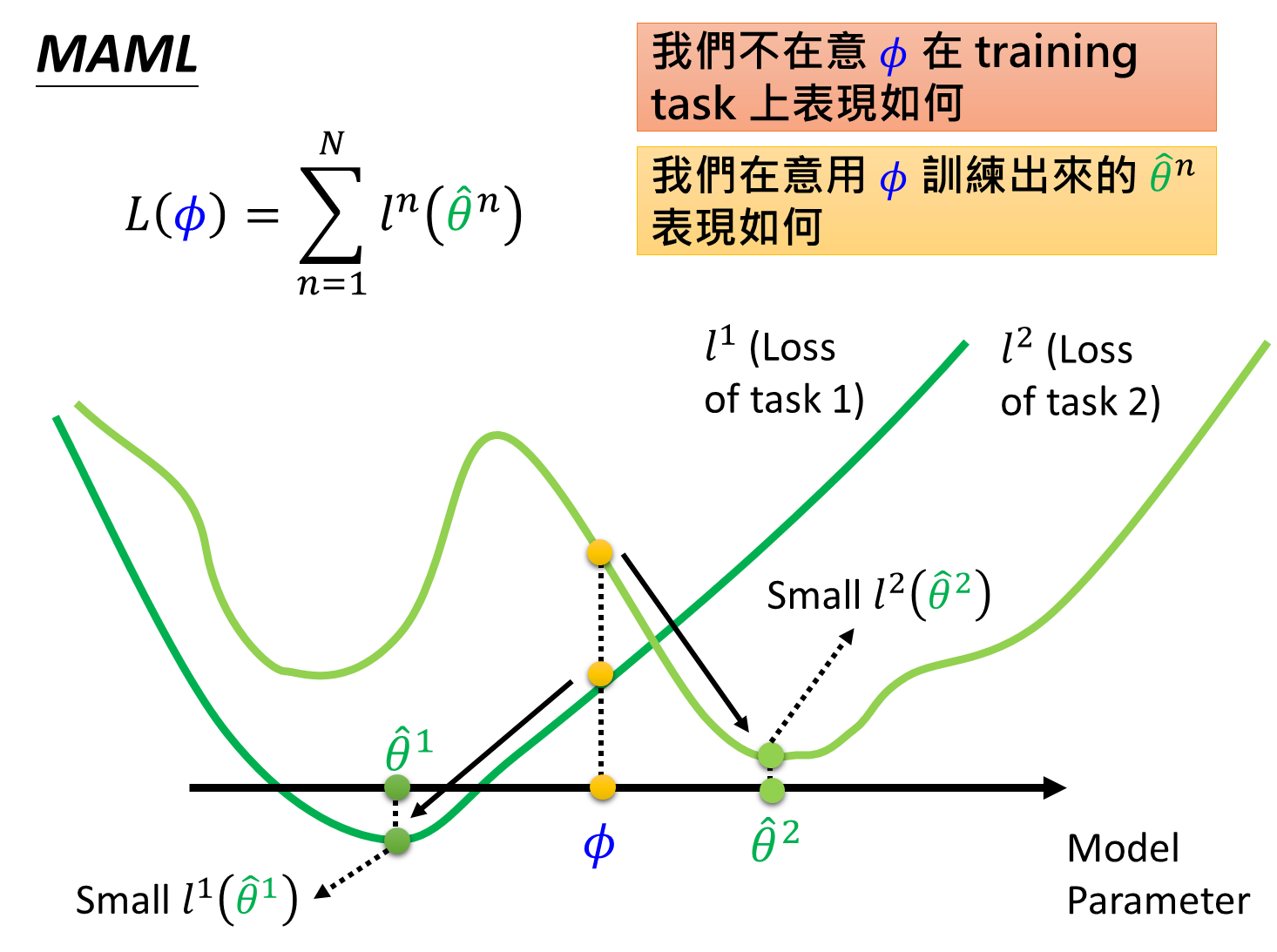
用论文中图片来说就是找到一个$\varphi$，在训练后可以让所有任务上loss都能下降到最优。

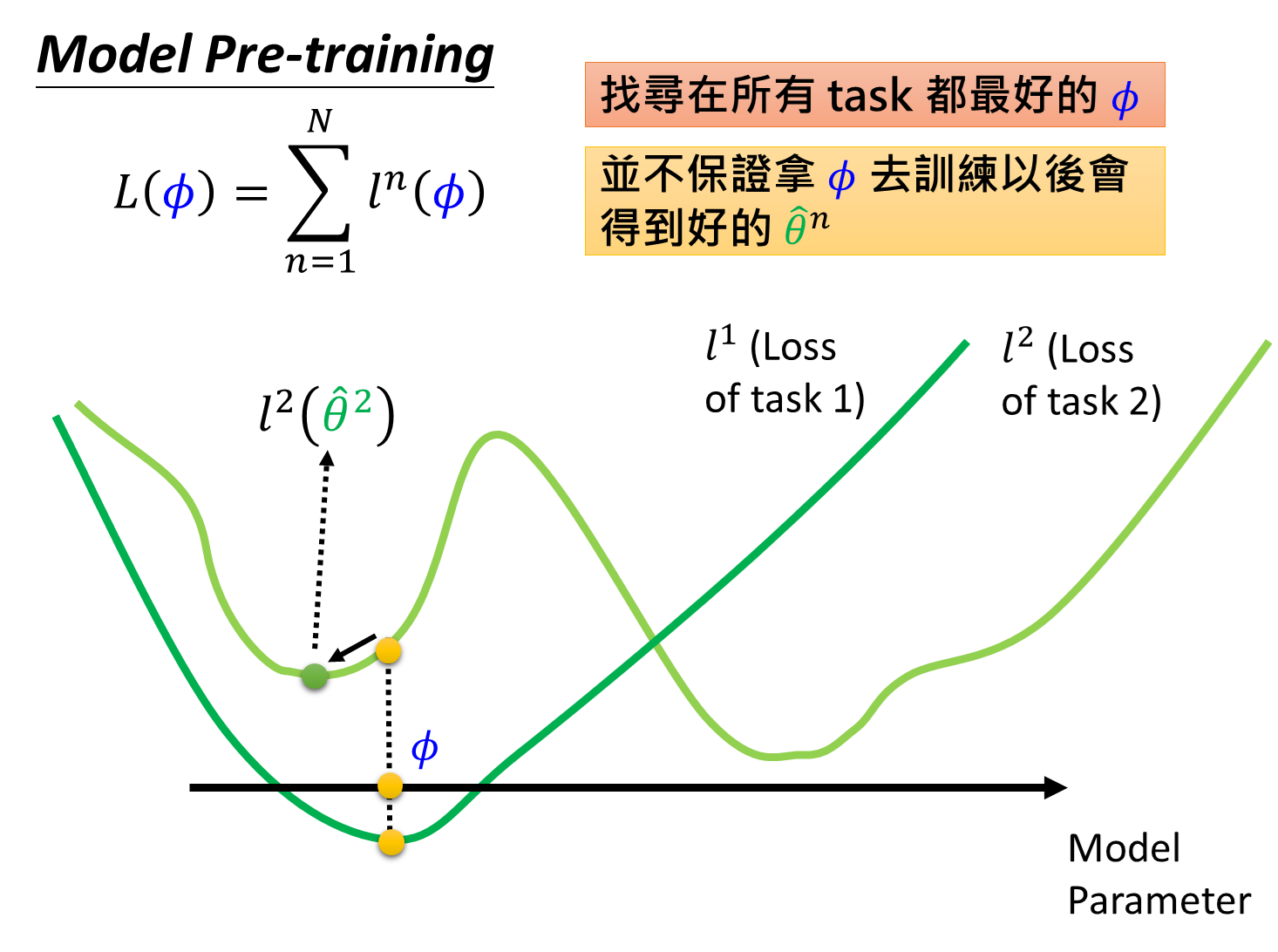
而model pre-training的初衷是寻找一个从一开始就让所有任务的损失之和处于最小状态 $\varphi$，它并不保证所有任务都能训练到最好的${\hat{\theta }}^n$ ，如上图所示， loss可能会收敛到局部最优。

MAML算法

$P(T)$用来表示任务的分布，$\beta ，\alpha$是训练的超参数，表示子任务内的学习率和任务间的学习率，$f_{\theta }$表示训练的模型。

1. 随机初始化模型参数$\theta$，这个$\theta$就是前文李宏毅老师所讲的${\varphi }_0$其实。
2. 每一次训练从中提取一个子任务$T_i$。
3. 在$T_i$任务里，我们使用公式${\theta }_i^{\prime }=\theta -\alpha {\nabla }_{\theta }{L}_{T_i}(f\theta )$ 来更新任务内的${\theta }_{}$