回溯算法深度解析：全排列、组合与剪枝应用-优快云博客

前面已经写过一篇博客记录回溯算法，然后今天再看回溯的题目的时候，发现自己可能仅仅理解了那个题目的意思但是并没有理解回溯算法的使用。没有理解到回溯算法的真正的内涵吧！所以再研究了一些题目之后我来做一个简单的记录！😀😀

一、什么是回溯？

顾名思义，回溯就是可以往回走的，也就是说在深度优先的基础上，我们可以通过一条路走到黑当没有办法再走下去的时候回退到它的前面一步甚至是前面n步

二、回溯和深度优先的区别在哪里？

①深度优先的每个节点只可以访问一次但是回溯可以访问多次

②回溯适用于树的求解，深度优先适用于图，也就是说深度优先的应用范围是大于回溯的

③回溯中使用了深度优先的思想+剪枝算法

三、回溯的理解

好了，有了上面的一些基础，我们就可以来通过题目理解回溯了，我们会先放上三个题目，然后博主会将三个题目放在一起进行比较，然后大家就可以发现，噢，原来回溯是这样，然后我们再来练几题就一切明了了！

（一）三个帮助理解的题目

1. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

拿到这个题目的时候，你能不能想到要用回溯算法？❓

我想，如果没有在这个专题下，也许有些同学想不到

我猜你第一个想法就是暴力破解，既然已经知道数组是不重复的，想要得到所有的解那还不简单，使用多重for循环就解决了，没错，是可以进行解决；但是你有没有发现局限性很大？【大家想想这里的局限性在哪里？】

局限在于，你的for循环的层数要根据你的数据的个数来定，比如你需要对三个数据进行全排列，那就需要三重for循环；由此可以知道，暴力求解虽然可以用，但是局限性真的很大，并且写起来复杂，时间复杂度就不用说了！

那么，我们怎么求解？这就需要大家回忆我们的回溯了，我们的回溯是不是走到最后一层，然后回退到上一层甚至是上上层，直到最后得到了所有的结果。这里需要的就是所有的可能，那是不是就是我们所需要的？

好，那么我们就用一个简单的案例来描述一下在这里回溯应该怎么使用，如下所示：

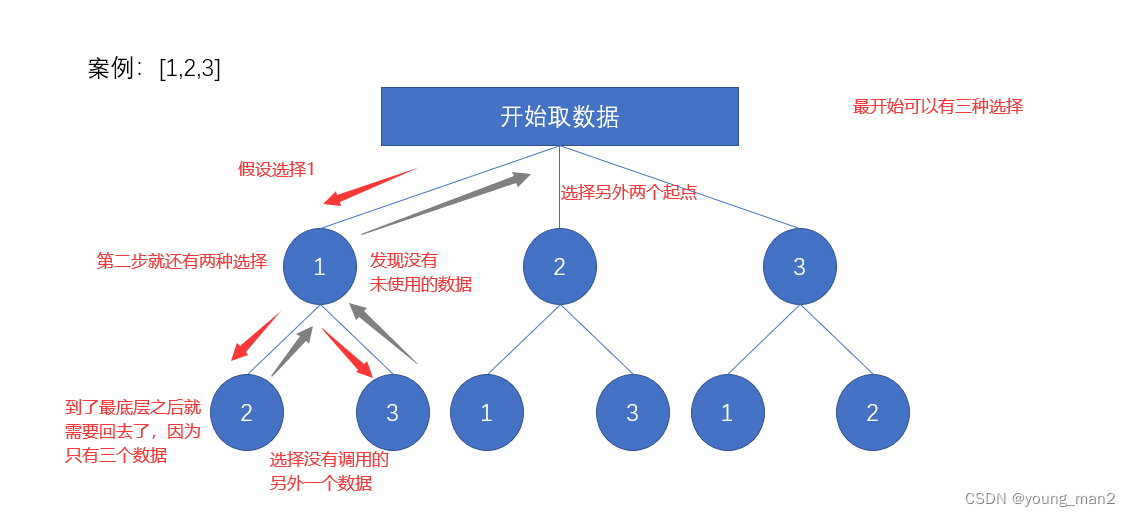
❗下面还有一层很抱歉没有画出来，但是应该算是显而易见吧，嘿嘿嘿❗

好了，从上面大家可以大概的猜到我们需要哪些数据吧？

①我们需要一个集合来存放当前的路径

②我们需要一个双重的集合来存放所有的路径

③我们需要一个数据来表示高度，也就是当我们遍历完节点之后需要进行一个回退

④我们需要一个数据来标识当前数据有没有被使用

然后我们就可以写代码了

class Solution {
     
    public List<List<Integer>> permute(int[] nums) {
       Solution solution=new Solution();
        int len=nums.length;

        List<List<Integer>> res=new ArrayList<>();
        //如果当前数组不存在的话，就返回空的数组
        if(len==0){
            return res;
        }
        //首先我们需要一个数组取表示当前数据有没有被读取
        boolean []used=new boolean[len];

        //然后我们需要一个数组来存储当前的路径,这里不写泛型是会自动补充泛型
        List path=new ArrayList<>();

         solution.dfs(nums,len,res,0,path,used);
        return res;

    }

    public void dfs(int[] nums,int len,List<List<Integer>> res,int depth,List path, boolean[] used)   {
        if (depth == len ){
            res.add(new ArrayList(path));
            return ;
        }

        for(int i=0;i<len;i++){
            if (!used[i]) {
                    path.add(nums[i]);
                    used[i] = true;

                    dfs(nums, len,res,depth+1, path, used);
                    // 注意：下面这两行代码发生 「回溯」，回溯发生在从 深层结点 回到 浅层结点 的过程，代码在形式上和递归之前是对称的
                    used[i] = false;

                    path.remove(path.size() - 1);
                }
        }
    

    }
}

2. 全排列Ⅱ

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

和上面的类似，但是这里有一个什么条件呢？就是我给的数组里面是可以包含重复的数据的

那么应该怎么求解？

这里要解决的就是在上面的基础上我们要排除重复数据！

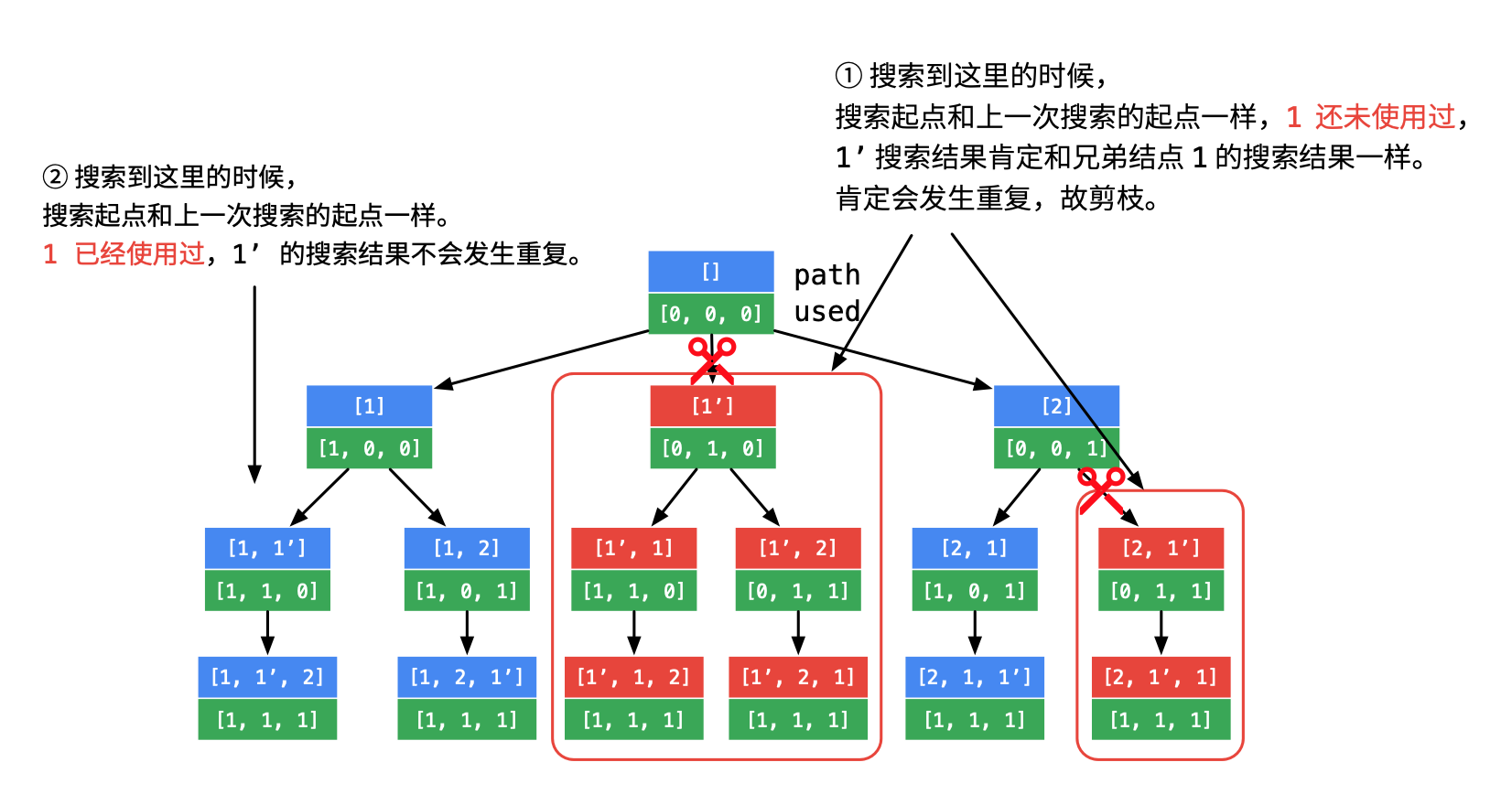
public class Solution {

    public List<List<Integer>> permuteUnique(int[] nums) {
        int len = nums.length;
        List<List<Integer>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }

        // 排序（升序或者降序都可以），排序是剪枝的前提
        Arrays.sort(nums);

        boolean[] used = new boolean[len];
        // 使用 Deque 是 Java 官方 Stack 类的建议
        Deque<Integer> path = new ArrayDeque<>(len);
        dfs(nums, len, 0, used, path, res);
        return res;
    }

    private void dfs(int[] nums, int len, int depth, boolean[] used, Deque<Integer> path, List<List<Integer>> res) {
        if (depth == len) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = 0; i < len; ++i) {
            if (used[i]) {
                continue;
            }

            // 剪枝条件：i > 0 是为了保证 nums[i - 1] 有意义
            // 写 !used[i - 1] 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
                continue;
            }

            path.addLast(nums[i]);
            used[i] = true;

            dfs(nums, len, depth + 1, used, path, res);
            // 回溯部分的代码，和 dfs 之前的代码是对称的
            used[i] = false;
            path.removeLast();
        }
    }
}

其实这里很巧妙的一个地方就在于这里

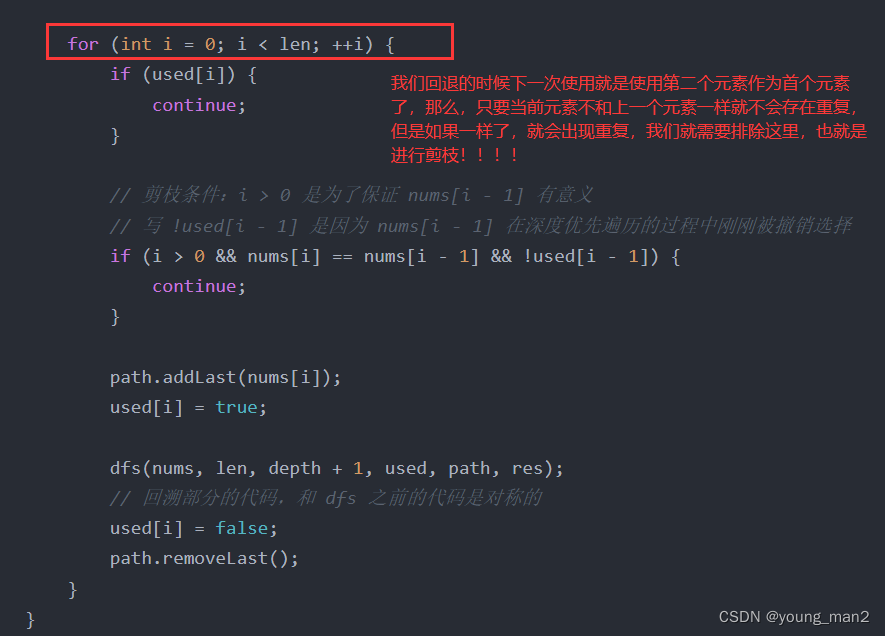
3. 组合总和

给你一个无重复元素的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些组合。

candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

在这里，我们看到，我们需要得到结果的所有组合，也是和前面全排列一样，需要得到所有的结果！

但是在这里不同的是，数组中的元素是可以重复使用的，就不再需要上面的used数组了！

class Solution {

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }

        // 排序是剪枝的前提
        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, len, target, path, res);
        return res;
    }

    private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) {
        // 由于进入更深层的时候，小于 0 的部分被剪枝，因此递归终止条件值只判断等于 0 的情况
        if (target == 0) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = begin; i < len; i++) {
            // 重点理解这里剪枝，前提是候选数组已经有序，
            if (target - candidates[i] < 0) {
                break; 
            }
            
            path.addLast(candidates[i]);
            dfs(candidates, i, len, target - candidates[i], path, res);
            path.removeLast();
        }
    }
}

（二）对比

好了，有了上面三个题目的基础，我们就可以吧这三个题目进行一个简单的对比了，我们将三个题目的代码放在一起进行比较，如下所示：

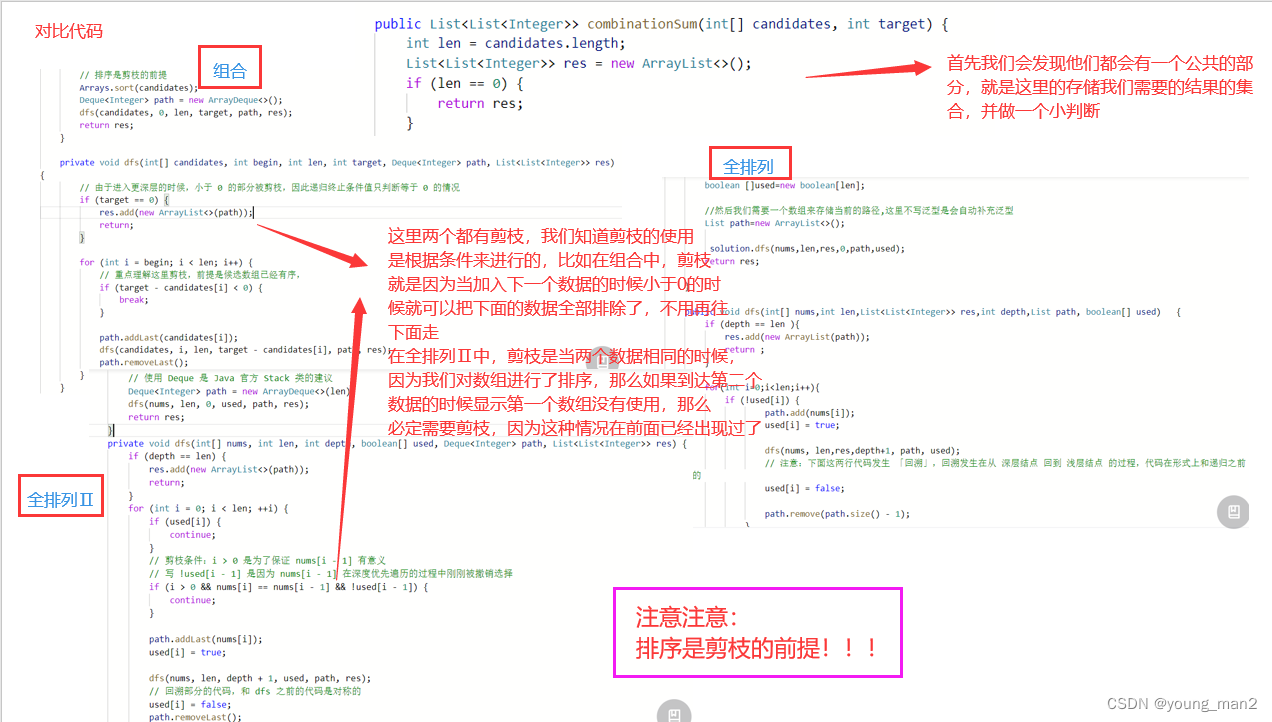
根据上面的三个题目，我们可以知道，当需要我们求得所有解或者在所有解的基础上需要进行一些操作的时候，我们就可以使用剪枝！总而言之，就是只要涉及求全部解的时候就可以使用回溯！！

什么时候使用剪枝，当有一些条件需要进行排除的时候我们就可以使用剪枝！

（三）升级练习

那么，有了上面的三个题目，大家应该对回溯有了一些的了解，那么接下来我将放出几个题目来给大家作为练习，希望大家在尝试后再看答案！

1. 组合总和Ⅱ

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

class Solution {

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }

        // 关键步骤
        Arrays.sort(candidates);

        Deque<Integer> path = new ArrayDeque<>(len);
        dfs(candidates, len, 0, target, path, res);
        return res;
    }

    /**
     * @param candidates 候选数组
     * @param len        冗余变量
     * @param begin      从候选数组的 begin 位置开始搜索
     * @param target     表示剩余，这个值一开始等于 target，基于题目中说明的"所有数字（包括目标数）都是正整数"这个条件
     * @param path       从根结点到叶子结点的路径
     * @param res
     */
    private void dfs(int[] candidates, int len, int begin, int target, Deque<Integer> path, List<List<Integer>> res) {
        if (target == 0) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = begin; i < len; i++) {
            // 大剪枝：减去 candidates[i] 小于 0，减去后面的 candidates[i + 1]、candidates[i + 2] 肯定也小于 0，因此用 break
            if (target - candidates[i] < 0) {
                break;
            }

            // 小剪枝：同一层相同数值的结点，从第 2 个开始，候选数更少，结果一定发生重复，因此跳过，用 continue
            if (i > begin && candidates[i] == candidates[i - 1]) {
                continue;
            }

            path.addLast(candidates[i]);
            // 调试语句 ①
            // System.out.println("递归之前 => " + path + "，剩余 = " + (target - candidates[i]));

            // 因为元素不可以重复使用，这里递归传递下去的是 i + 1 而不是 i
            dfs(candidates, len, i + 1, target - candidates[i], path, res);

            path.removeLast();
            // 调试语句 ②
            // System.out.println("递归之后 => " + path + "，剩余 = " + (target - candidates[i]));
        }
    }
}

2. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        //对于这个题目，得到所有的解，也可以使用回溯进行求解，只是他需要的是所有的可能性，那么我们要做的就是
        //到达最下面的时候进行一个删除回溯就行，也就是使用for循环进行一个简单的限制
        //我们需要什么变量？起始的位置、存放数据的集合、存放集合的集合、数组的长度
        int length=nums.length;
        //这里不会存在数组为空的情况，因为数组就算为空也可以进行输出，不用判断
        List<List<Integer>> res=new ArrayList<>();
        ArrayList<Integer> path=new ArrayList<>();
        dfs(0,length,nums,res,path);
        return res;

    }

    public void dfs(int begin,int len,int nums[],List<List<Integer>> res, ArrayList<Integer> pom){
        //这里首先把[]的情况添加进去
        res.add(new ArrayList<>(pom));
        for(int i=begin;i<len;i++){
            pom.add(nums[i]);
            dfs(i+1,len,nums,res,pom);
            pom.remove(pom.size()-1);
        }
    }
}

3. 子集Ⅱ

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。返回的解集中，子集可以按任意顺序排列。

class Solution {
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        //这里涉及去重，我们应该怎么去重，我们可以判断后一个数据和前一个数据是不是相等，相等的话就不添加
        //那么就可以添加一个限制条件 如果没有被使用过，同时前面等于后面就删除
        List<List<Integer>> res=new ArrayList<>();
        ArrayList<Integer> path=new ArrayList<>();
        int length=nums.length;
        boolean []used=new boolean[length];
        Arrays.sort(nums);
        dfs(0,length,used,nums,res,path);
        return res;
    }
    public void dfs(int begin,int len,  boolean used[],int []nums,List<List<Integer>> res,ArrayList<Integer> path){
        res.add(new ArrayList(path));
        for(int i=begin;i<len;i++){
            
            if(i>0 && nums[i]==nums[i-1] && !used[i-1]){
                continue;
            }
            path.add(nums[i]);
            used[i]=true;
            dfs(i+1,len,used,nums,res,path);
            used[i]=false;
            path.remove(path.size()-1);
        }

    }
}

❗注意❗

排序是剪枝的前提，所以别忘记！！！

4. 组合总和Ⅲ

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9
每个数字最多使用一次
返回所有可能的有效组合的列表。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

class Solution{
public List<List<Integer>> combinationSum3(int k, int n) {
         List<List<Integer>> res = new ArrayList<>();
        Deque<Integer> path = new ArrayDeque<>();//存储根节点开始的路径
        dfs3(1, k, path, n, res);
        return res;
    }

    public static void dfs3(int begin, int k, Deque<Integer> path, int target, List<List<Integer>> res) {
        // 1.结束条件
        if (target == 0 && path.size() == k) {
            res.add(new ArrayList<Integer>(path));
            return;
        }

        // 2.选择列表
        for (int i = begin; i < 10; i++) {
            // 大剪枝
            if (target - i < 0) return;
            // 选择
            path.addLast(i);
            // 递归
            dfs3(i + 1, k, path, target - i, res);
            // 撤销选择
            path.removeLast();
        }
    }
}

5. 单词搜索

【关于增强for循环中二维数组的一些使用】

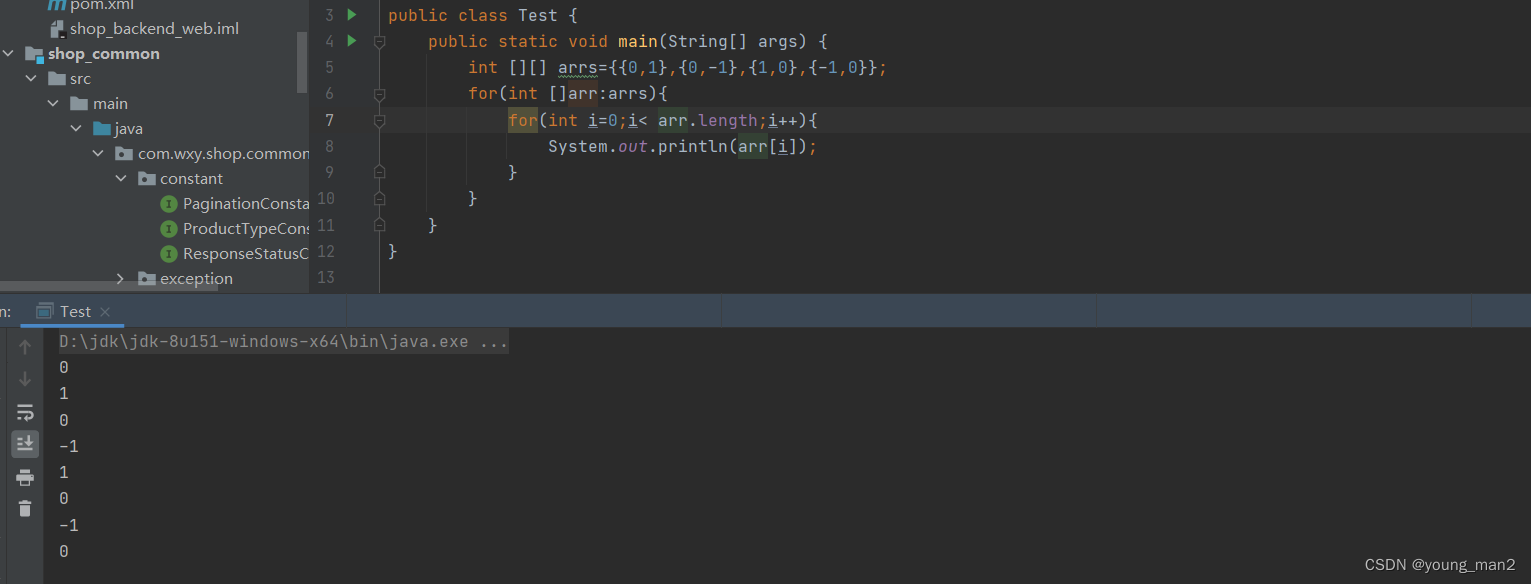
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

class Solution {
    public boolean exist(char[][] board, String word) {
        //这个题目也是回溯算法的典型
        //主要思想为，我们从(1,1)开始往后找，可以知道他只可以向下或者向右
        //那么我们就可以先选择向下走，如果当前走不通就返回，走之前路径允许的下一步，如果在可以走的所有步骤里面都走不完就返回false
        //我们还需要设置一个变量，used来保证我们走过的点不重复走
        if(word.length()==0)
            return false;
        //我们首先获取board的长和宽
        int h=board.length;
        int w=board[0].length;
         boolean[][] visited = new boolean[h][w];
        //使用双重遍历来实现我们的可以从所有的点开始
        for(int i=0;i<h;i++){
            for(int j=0;j<w;j++){
                boolean flag=huisu(board,i,j,word,0,visited);
                if(flag){
                    return true;
                }
            }
        }
        return false;
    }

    public boolean huisu(char[][]board,int i,int j,String s,int k,boolean visited[][]){
        //首先我们要给一个结束条件，就是当我们当前位置上的元素和word的第k个元素不相等的时候，返回false
        //如果k到达我们的String的长度，就说明匹配成功
        if(board[i][j]!=s.charAt(k)){
            return false;
        }
        else if(k==s.length()-1){
            return true;
        }
        visited[i][j]=true;
        boolean result=false;
        //下面就开始正式的遍历
        //我们首先需要一个二维数组来表示上下左右移动
        int[][] arrays={{0,1},{0,-1},{1,0},{-1,0}};   //上下左右
        for(int []arr : arrays){
            int newi = i+arr[0];
            int newj = j+arr[1];

            if (newi >= 0 && newi < board.length && newj >= 0 && newj < board[0].length) {
                if (!visited[newi][newj]) {
                    boolean flag = huisu(board,  newi, newj, s, k + 1,visited);
                    if (flag) {
                        result = true;
                        break;
                    }
                }
            }
        }
        visited[i][j]=false;
        return result;

    }
}