数数 蓝桥杯

---

---

解题思路

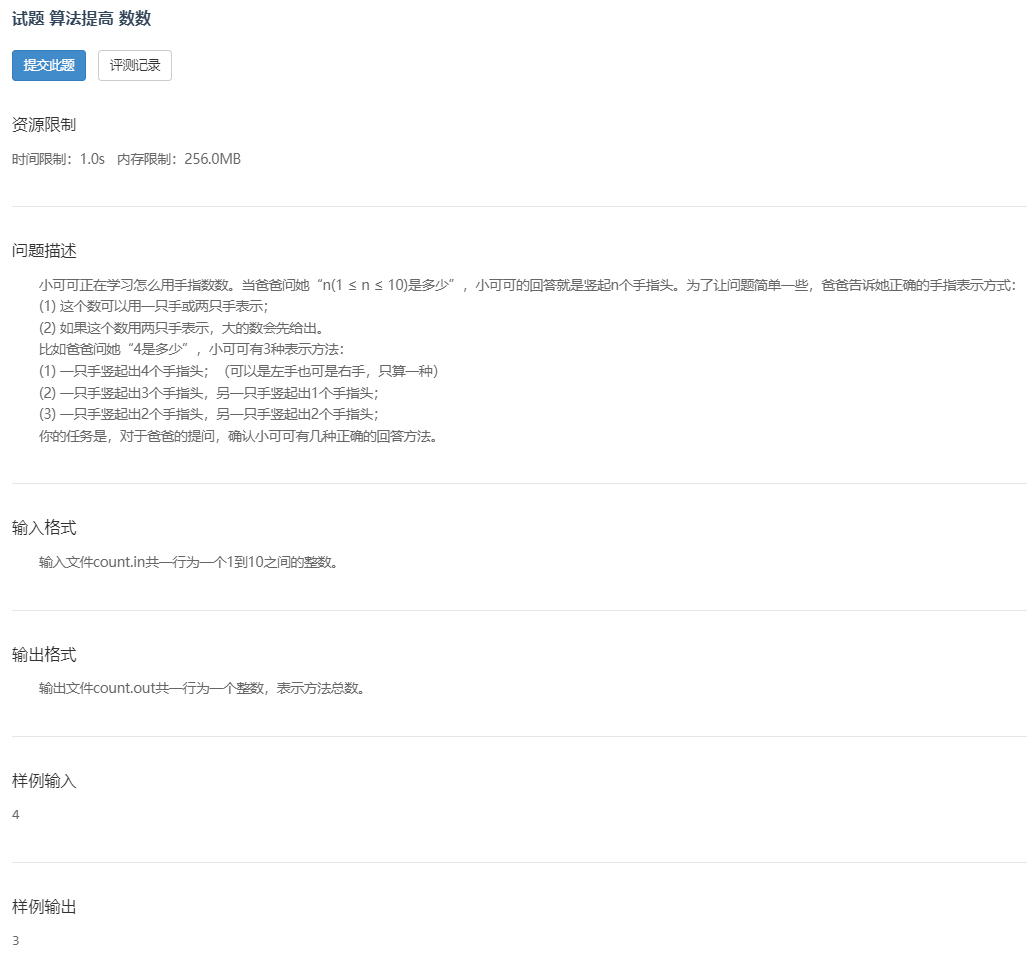
这个题比较水，输入数据 n 的取值范围为1~10，范围很少，可以直接用switch选择结构根据n的值输出结果。只需要我们事先计算出结果即可，这个结果也不难求，很快就算出来了，计算过程就不讲解了。

代码

#include<iostream>
using namespace std;
int main(){
    int n;
    cin >> n;
    switch (n)
    {
    case 1:
    case 9:
    case 10:
        cout << 1 << endl;
        break;
    case 2:
    case 3:
    case 7:
    case 8:
        cout << 2 << endl;
        break;
    case 4:
    case 5:
    case 6:
        cout << 3 << endl;
        break;
    }
    return 0;
}