基于AI的开源项目工作量预测

5 基于工作量预测模型和人工智能的开源项目故障大数据分析

5.1 引言

近年来，各种开源软件（OSS）被广泛应用于许多软件系统和服务中。此外，由于快速交付、标准化、成本降低等原因，许多软件系统都通过使用多个OSS组件进行开发。因此，过去[1–3]年间已提出了多种针对OSS系统的软件可靠性增长模型。

本章讨论了若干考虑维纳过程和人工智能的开源软件项目工作量预测模型，以理解开源软件项目的多个外部因素。特别是，我们讨论了跳跃扩散过程模型。然后，介绍了遗传算法的方法

算法（GA）、深度学习和最大似然被用作基于人工智能的随机微分方程（SDE）模型的参数估计方法。

此外，本章利用所提出的开源项目（OSS）实际故障大数据工作量预测模型，给出了多个基于实际故障大数据的数值示例。接着，本章讨论了基于人工智能（AI）的参数估计的数值图示。最后，我们证明了所提出的工作量预测模型有助于预测开源项目下开发的开源软件质量和可靠性的软件工作量。

5.2 基于跳跃扩散过程的灵活工作量预测模型

我们讨论了利用跳跃扩散过程来控制运行期间的开源软件维护工作量。设 $ Z(t) $ 为在运行期间截至时间 $ t (t \geq 0) $ 的累计开源软件维护工作量支出。$ Z(t) $ 为连续的实数值。由于维护工作量是在开源软件运行过程中记录的，因此随着开源软件运行进展，$ Z(t) $ 逐渐增加。通过使用经典软件可靠性建模[4–7]的建模技术，可得如下考虑开源软件维护工作量的方程：

$$
\frac{dZ(t)}{dt} = \beta(t){ \alpha - Z(t) }, \quad (5.1)
$$

其中 $ \beta(t) $ 表示开源软件在时间 $ t $ 的工作量支出率。$ \alpha $ 表示在指定版本期间所支出的估计的维护工作量。

考虑到布朗运动，公式(5.1)可表示为以下随机微分方程[8, 9]:

$$
\frac{dZ(t)}{dt} = { \beta(t) + \sigma\nu(t) }{ \alpha - Z(t) }, \quad (5.2)
$$

其中 $ \sigma $ 被添加为一个正值，表示不规则连续波动的水平，$ \nu(t) $ 为由于开发环境引起的标准化高斯白噪声。然后，公式(5.2)被扩展为以下 Itô 类型的随机微分方程：

$$
dZ(t) = \left{ \beta(t) - \frac{1}{2} \sigma^2 \right}{ \alpha - Z(t) }dt + \sigma { \alpha - Z(t) }dw(t), \quad (5.3)
$$

其中，$ w(t) $ 表示一维维纳过程。$ w(t) $ 可表示为白噪声 $ \nu(t) $。

跳跃项通过考虑在时间 $ t $ 时由许多外部复杂项目因素引起的意外不规则情况，被嵌入到公式(5.3)的SDE模型中。跳跃扩散过程如下所示：

$$
dZ_j(t) = \left{ \beta(t) - \frac{1}{2} \sigma^2 \right}{ \alpha - Z_j(t) }dt + \sigma { \alpha - \Psi_j(t) }dw(t) + d \sum_{i=1}^{Y(\lambda)} (V_i - 1), \quad (5.4)
$$

其中，在时间 $ t $ 处频率为 $ \lambda $ 的泊松点过程表示为 $ Y_t(\lambda) $，即跳跃次数，$ \lambda $ 为跳跃率。$ V_i $ 表示第 $ i $ 次跳跃的范围。我们假设 $ w(t) $、$ Y_t(\lambda) $ 和 $ V_i $ 相互独立。此外，开源软件维护工作量在 $ \beta(t) $ 的增长率如下所示

$$
\int_0^t \beta(s)ds = \frac{dR^ (t)}{dt} { \alpha - R^ (t) }, \quad (5.5)
$$

$$
R_e(t) = a(1 - e^{-bt}), \quad (5.6)
$$

$$
R_s(t) = a(1 - (1 + bt)e^{-bt}). \quad (5.7)
$$

在本章中，$ \beta(t) $ 假设为来自非齐次泊松过程（NHPP）模型的公式(5.6)和(5.7)中的均值函数，作为我们模型的开源软件工作量支出函数，其中 $ =. \alpha $ 是潜在故障的预期累积数量，$ =. \beta $ 是根据软件可靠性增长模型得出的每故障检测率。

基于 Itô 公式[10], $ Z_j^*(t) $ 可由公式(5.4)推导得出

$$
Z_{je}(t) = \alpha \left[ 1 - \exp \left{ -\beta t - \sigma w(t) - \sum_{i=1}^{Y_t(\lambda)} \log V_i \right} \right], \quad (5.8)
$$

$$
Z_{js}(t) = \alpha \left[ 1 - (1 + \beta t) \exp \left{ -\beta t - \sigma v(t) - \sum_{i=1}^{Y_t(\lambda)} \log V_i \right} \right]. \quad (5.9)
$$

此外，我们将从公式(5.4)得到的现有跳跃扩散过程模型扩展到以下时滞跳跃扩散过程：

在 $ t \geq 0 $ 的情况下：

$$
dZ_{fj}(t) = \left{ \beta(t) - \frac{1}{2} \sigma^2 \right}{ \alpha - Z_{fj}(t) }dt + \sigma { \alpha - Z_{fj}(t) }dw(t) + d \sum_{i=0}^{Y_t(\lambda_1)} (V_{1i} - 1), \quad (5.10)
$$

若 $ t \geq 0 $ 且 $ t’ \geq 1[t] $:

$$
dZ_{fj}(t) = \left{ \beta(t) - \frac{1}{2} \sigma^2 \right}{ \alpha - Z_{fj}(t) }dt + \sigma { \alpha - Z_{fj}(t) }dw(t)
+ d \sum_{i=0}^{Y_t(\lambda_1)} (V_{1i} - 1) + d \sum_{i=0}^{Y_{t’}(\lambda_2)} (V_{2i} - 1), \quad (5.11)
$$

其中，$ Y_t(\lambda_1) $ 和 $ Y_{t’}(\lambda_2) $ 分别为在运行时间 $ t \geq 0 $ 和 $ t’ \geq 1[t] $ 处参数为 $ \lambda_1 $ 和 $ \lambda_2 $ 的泊松点过程。此外，$ V_{1i} $ 和 $ V_{2i} $ 分别为在运行时间 $ t \geq 0 $ 和 $ t’ \geq 1[t] $ 处的第 $ i $ 次跳跃范围。本文假设 $ Y_t(\lambda_1) $、$ Y_t(\lambda_2) $、$ V_{1i} $ 和 $ V_{2i} $ 相互独立。

根据伊藤公式，方程(5.10)和(5.11)的解可如下获得：

当 $ t \geq 0 $ 时：

$$
Z_{fje}(t) = \alpha \left[ 1 - \exp \left{ -\beta t - \sigma w(t) - \sum_{i=1}^{Y_t(\lambda_1)} \log V_{1i} \right} \right], \quad (5.12)
$$

$$
Z_{fjs}(t) = \alpha \left[ 1 - (1 + \beta t) \cdot \exp \left{ -\beta t - \sigma w(t) - \sum_{i=1}^{Y_t(\lambda_1)} \log V_{1i} \right} \right]. \quad (5.13)
$$

当 $ t \geq 0 $ 且 $ t’ \geq 1[t] $ 时：

$$
Z_{fje}(t) = \alpha \left[ 1 - \exp \left{ -\beta t - \sigma w(t) - \sum_{i=1}^{Y_t(\lambda_1)} \log V_{1i} - \sum_{i=1}^{Y_{t’}(\lambda_2)} \log V_{2i} \right} \right], \quad (5.14)
$$

$$
Z_{fjs}(t) = \alpha \left[ 1 - (1 + \beta t) \cdot \exp \left{ -\beta t - \sigma w(t) - \sum_{i=1}^{Y_t(\lambda_1)} \log V_{1i} - \sum_{i=1}^{Y_{t’}(\lambda_2)} \log V_{2i} \right} \right]. \quad (5.15)
$$

考虑到 $ t_2 \geq t_1 (t \geq 1) $ 上的时间延迟，我们可以将灵活跳跃扩散过程模型表述如下：

$$
Z_{fje}(t) = \alpha \left[ 1 - \exp \left{ -\beta t - \sigma w(t) - \sum_{k=1}^{K} \sum_{i=1}^{Y_{t_k}(\lambda_k)} \log V_{ki} \right} \right], \quad (5.16)
$$

$$
Z_{fje}(t) = \alpha \left[ 1 - (1 + \beta t) \exp \left{ -\beta t - \sigma w(t) - \sum_{k=1}^{K} \sum_{i=1}^{Y_{t_k}(\lambda_k)} \log V_{ki} \right} \right], \quad (5.17)
$$

其中 $ t_k (k = 1, 2, …, K) $ 表示第 $ k $ 次主版本升级的特定时间，$ K $ 为主版本升级的次数。

5.3 灵活工作量预测模型噪声参数的参数估计

5.3.1 漂移项的最大似然方法

本节中，我们对方程(5.16)和(5.17)中的若干未知参数 $ \alpha $、$ \beta $、$ b $ 和 $ \sigma_1 $ 进行估计。注意 $ \sigma_2 $ 和 $ l $ 是已知参数，因为 $ \sigma_2 $ 和 $ l $ 作为网络因子获得。$ Z(t) $ 的联合概率分布函数定义为

$$
P(t_1, y_1; t_2, y_2; …; t_K, y_K) \equiv \Pr[Z(t_1) \leq y_1, …, Z(t_K) \leq y_K | Z(t_0) = 0]. \quad (5.18)
$$

由公式(5.18)可知，概率密度如下所示：

$$
p(t_1, y_1; t_2, y_2; …; t_K, y_K) \equiv \frac{\partial^K P(t_1, y_1; t_2, y_2; …; t_K, y_K)}{\partial y_1 \partial y_2 \cdots \partial y_K}. \quad (5.19)
$$

然后，为实际工作量数据 $ (t_k, y_k) (k = 1, …, K) $ 构造似然函数 $ \lambda $

$$
\lambda = p(t_1, y_1; t_2, y_2; …; t_K, y_K). \quad (5.20)
$$

作为数学处理技术，我们考虑以下对数似然函数：

$$
L = \log \lambda. \quad (5.21)
$$

然后，通过以下联立似然方程估计 $ \alpha^ $、$ \beta^ $、$ b^ $ 和 $ \sigma^ _1 $。接着，通过使公式(5.21)中的 $ L $ 最大化来给出这些估计值

$$
\frac{\partial L}{\partial \beta} = \frac{\partial L}{\partial b} = \frac{\partial L}{\partial \sigma_1} = 0. \quad (5.22)
$$

5.3.2 跳跃项的遗传算法方法

我们的模型包含混合分布，例如跳跃扩散和维纳过程。因此，由我们的模型构建出复杂的似然函数。于是，估计我们模型中跳跃项的未知参数变得困难。此外，过去已提出若干针对跳跃项中包含的未知参数的估计方法。然而，新颖的估计方法却鲜有提出。本节我们将讨论基于遗传算法的估计方法，以估计跳跃项中的未知参数。

我们跳跃模型的未知参数估计步骤如下：

然后，我们将 $ \gamma $、$ \mu $ 和 $ \tau $ 视为跳跃项中的未知参数。接着，参数 $ \mu $ 和 $ \tau $ 构成跳跃范围特别 $ V_i $。是，适应度函数由估计值和实际数据构成。本章节中定义了以下误差函数作为适应度函数，例如，估计值与实际值之间的误差：

$$
\min_\theta F_i(\theta),
$$

$$
F_i = \sum_{i=0}^{K} [Z_j(i) - y_i]^2,
$$

其中，$ M_j(i) $ 表示基于跳跃扩散过程的模型中在时刻 $ i $ 的累积软件操作工作量，$ y_i $ 表示累积软件工作量。此外，$ \theta $ 表示关于 $ \gamma $、$ \mu $ 和 $ \tau $ 的参数集。

上述过程应用于跳跃项的未知参数[11, 12]。

5.3.3 跳跃项的深度学习方法

我们使用最大似然法来估计未知参数 $ \alpha $、$ \beta $、$ b $ 和 $ \sigma $。特别是，由于似然函数中包含了基于维纳过程和跳跃扩散过程的多重分布，导致在我们的模型中对跳跃项的未知参数进行估计变得非常困难。特定研究人员已提出了针对跳跃扩散过程模型中跳跃参数的若干估计方法。然而，目前尚无有效的此类估计方法。本章节讨论涉及跳跃项的参数估计方法，并在本章中采用深度学习方法来确定所讨论模型的跳跃参数。

例如，我们假设跳跃扩散过程模型包含参数 $ \lambda_1 $ 和 $ \lambda_2 $ 用于 $ Y_t $ 和 $ Y_{t’} $，类似地，$ \mu_1 $、$ \mu_2 $、$ \tau_1 $ 和 $ \tau_2 $ 用于公式(5.16)和(5.17)中的 $ V_{1i} $ 和 $ V_{2i} $。然后，在 $ t \geq 0 $ 的情况下，通过深度学习算法对关于 $ \lambda_1 $、$ \mu_1 $ 和 $ \tau_1 $ 的参数集 $ J $ 进行估计。类似地，在 $ (t’ \geq t_1) $ 的情况下，使用深度学习算法对关于 $ \lambda_2 $、$ \mu_2 $ 和 $ \tau_2 $ 的参数集 $ J’ $ 做出决策。

本章中的深度学习结构如图5.1所示。在图5.1中，$ z_l (l = 1, 2, …, L) $ 和 $ z_m (m = 1, 2, …, M) $ 表示隐藏层中的预训练单元。此外，$ o_n (n = 1, 2, …, N) $ 是输出层的单元，作为压缩特征。在本章中，我们在多种深度学习算法中采用深度前馈神经网络，以学习缺陷跟踪系统中的开源软件故障大数据。我们针对输入层的每个单元应用以下输入数据集。然后，将作为目标变量的未知参数表示为关于 $ \lambda_1 $、$ \mu_1 $ 和 $ \tau_1 $ 的参数集 $ J $。以下九项解释变量被设置为输入层的单元：

• 日期和时间
• 开源软件产品名称
• 开源软件组件名称
• 开源软件版本名称
• 报告者（昵称）
• 负责人（昵称）
• 故障状态
• 操作系统名称
• 故障严重程度级别

然后，每个输入单元的输入值将从字符更改为数值[13]。

5.4 数值示例

Apache软件基金会的Apache HTTP服务器[14]是知名的开源软件。图5.2是基于遗传算法（GA）使用指数型工作量预测模型估算的运行人力支出。此外，点划线表示从6.x版本主线进行大版本升级的7.0.0测试版的起始时间线。从图5.2可以看出，在1,826天时间点之后，跳跃幅度变得较大。类似地，图5.3表示基于遗传算法（GA）使用S型工作量预测模型估算的累积OSS运维人力支出。从图5.3可以看出，S型工作量预测模型比指数型工作量预测模型更符合实际数据集的情况，其中长划线表示在图5.2和图5.3中从3.x版本主线进行大版本升级的4.1.31版本的起始时间线。

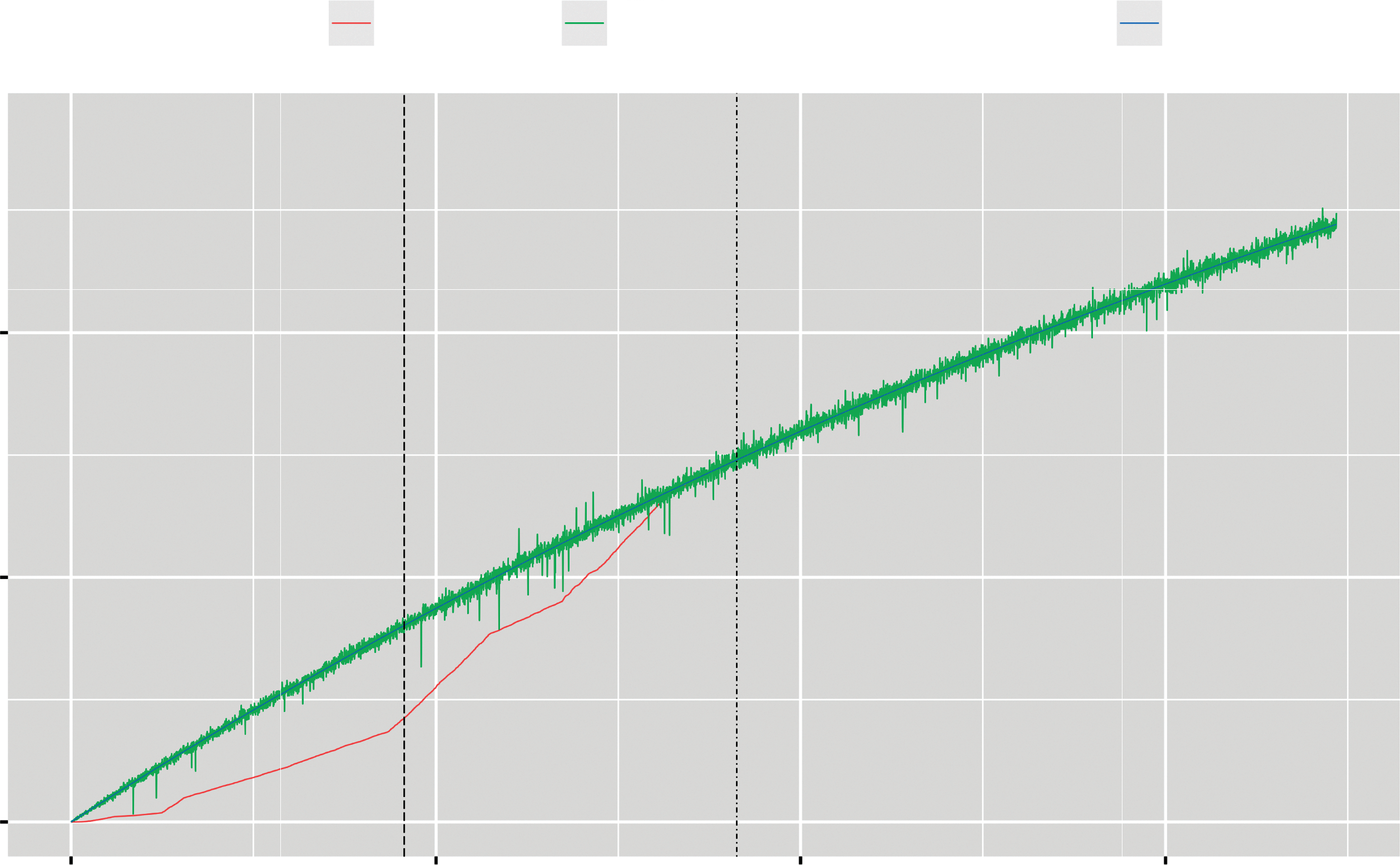
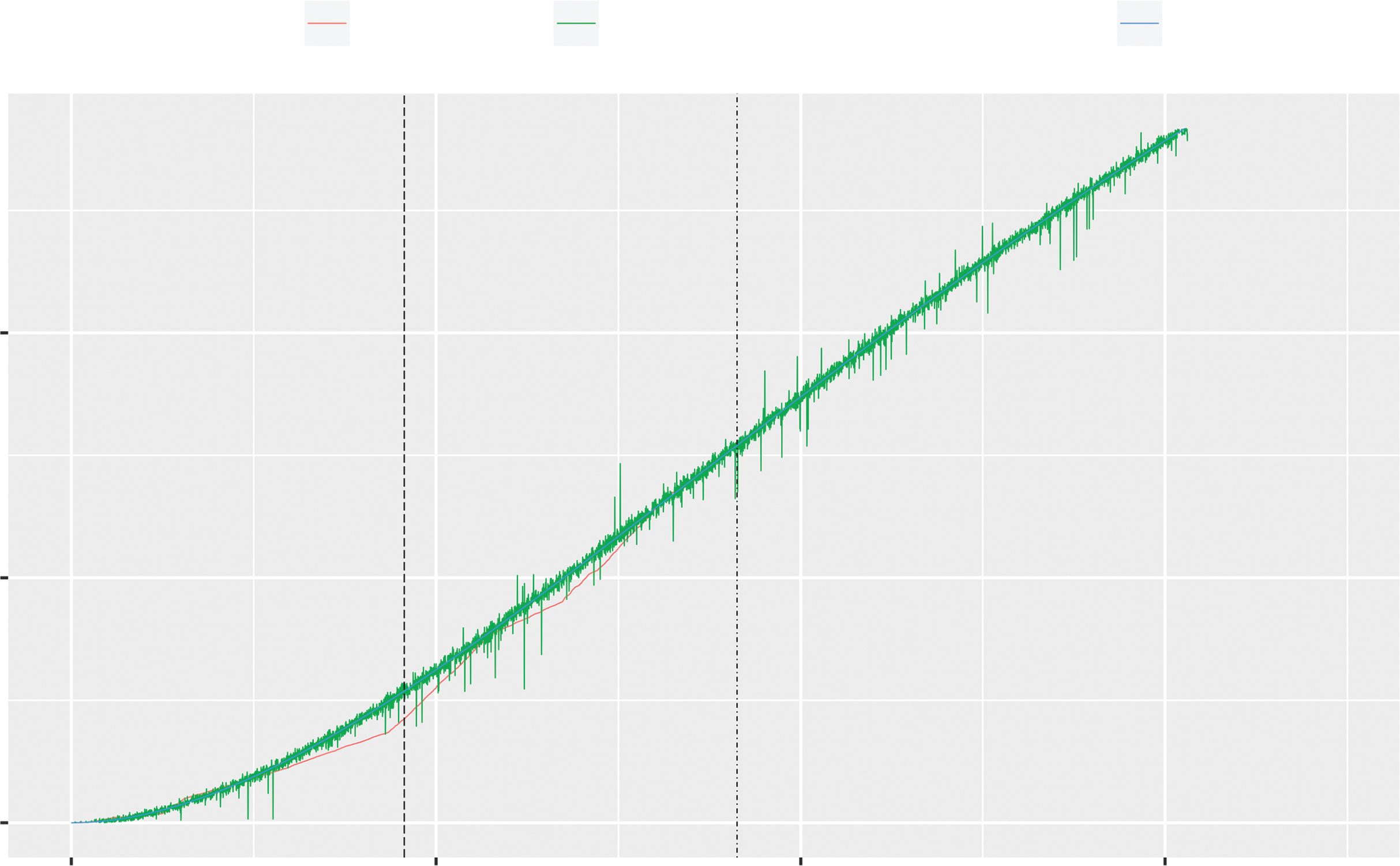
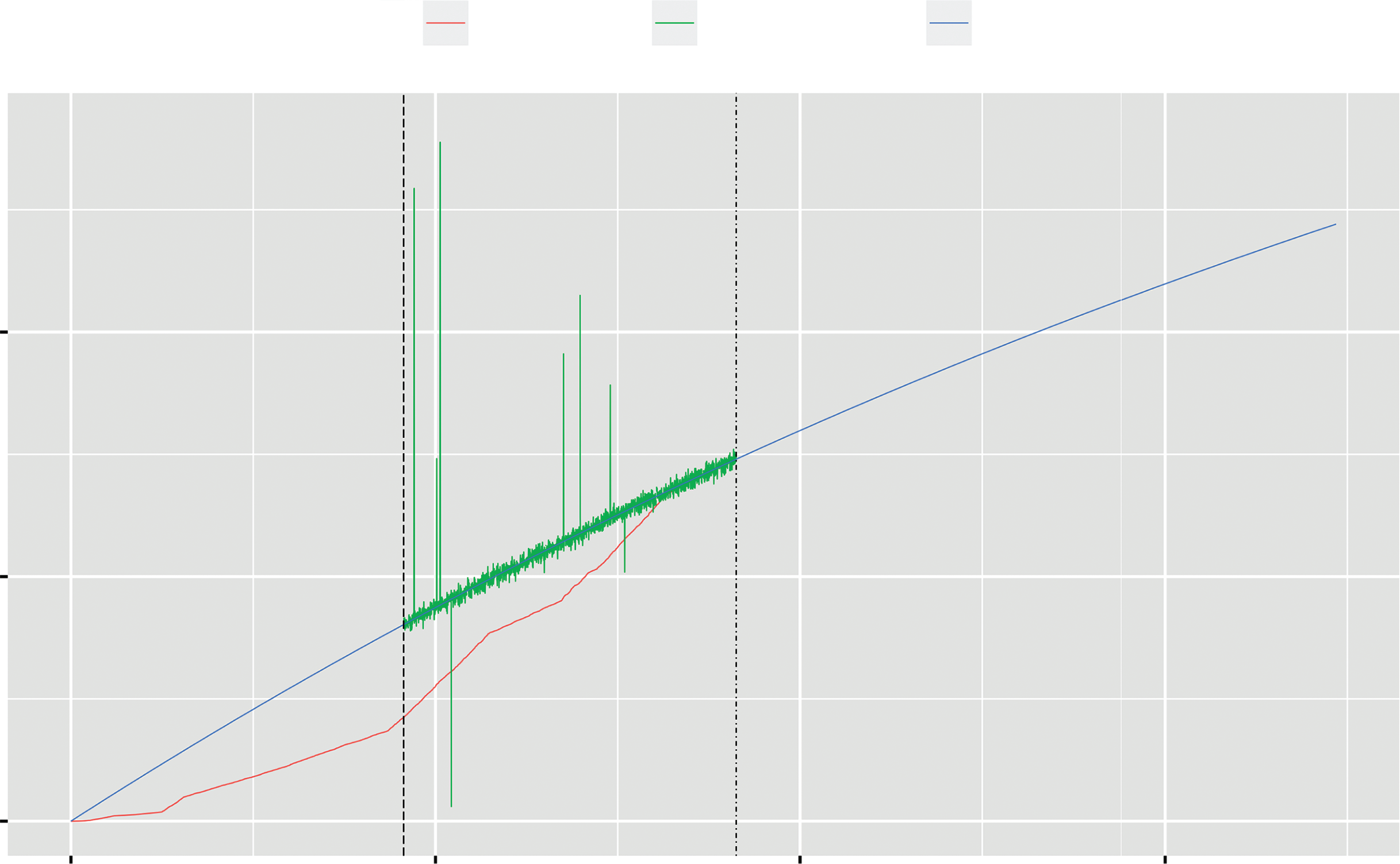
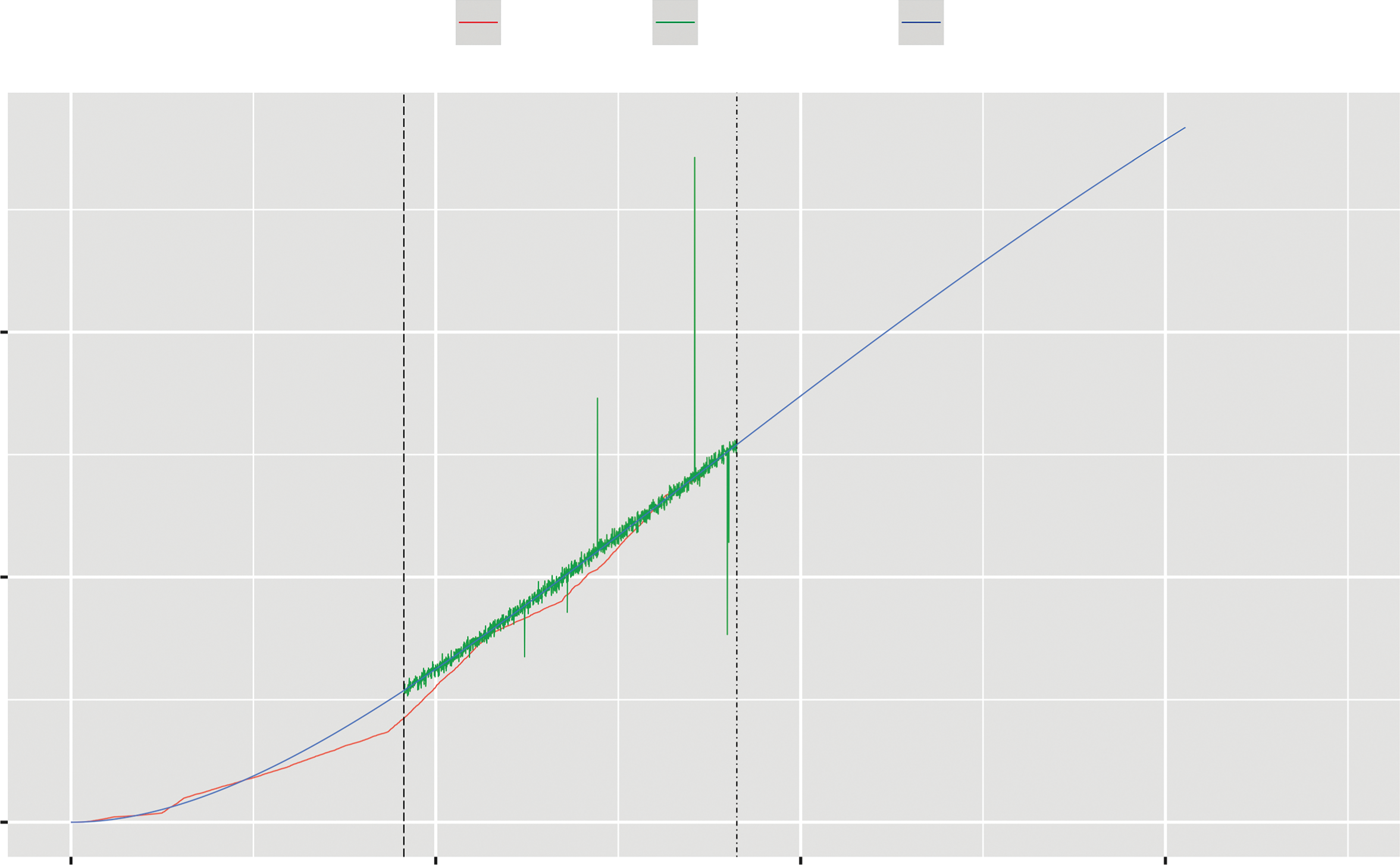
类似地，图5.4和图5.5展示了基于指数型工作量预测模型并使用深度学习方法估算的累积OSS运维人力支出，以及基于S型工作量预测模型并使用深度学习方法估算的累积维护工作量支出。特别是，在图5.4和图5.5中，指定阶段的数据集通过深度学习进行了估算。从图5.4和图5.5可以看出，深度学习的估计结果能够详细展示每个阶段的情况。

5.5 结论

本章节重点讨论开源软件项目中的软件工作量控制。开源软件工作量的最优估计与开源软件质量、开源软件可靠性以及开源软件成本降低有间接关系。在本章节中，我们讨论了考虑包含多次开源软件版本升级特征中非正常情况及跳跃项的开源软件工作量评估方法。对于开源软件项目经理而言，估计跳跃项的多个参数是困难的。因此，我们讨论了在工作量预测模型中使用的几种参数估计方法。所提出的参数估计方法将有助于从项目管理的角度，作为开源软件版本升级过程中进度的估计方法。