算法设计 ----网络流------二分匹配

一、介绍几个概念

• Matching:    Given 一个无向图G(V,E)，M是E的一个子集，若G中的每个节点至多出现在M中的一条边上，就说M是一个Matching。
• Max Matching：G中最大规模的匹配。
• bipartitle：无向图、节点集合可以被划分为两个集合L和R、图中的每个边e的一个端点在L中，另一个端点在R中。
• Bipartitle matching：Given 一个二部图，找到它的一个最大匹配。（在二部图中寻找一对一的匹配问题）

二、使用最大流问题的算法找最大匹配

• 构造流网络：

  

 

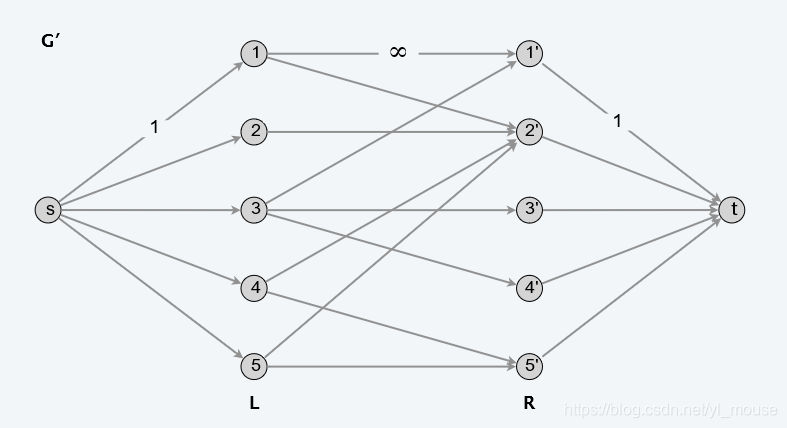
将二部图G构造为如上的图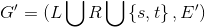，L到R的边添加方向L->R，s->L，R->t。

Theorem： 1–1 correspondence between matchings of cardinality k in G  and integral flows of value k in Gʹ.