老卫带你学---目标函数与损失函数的区别

损失函数度量的是预测值与真实值之间的差异。损失函数通常写作L(y^ ,y ),y^ 代表预测值，y代表真实值。例如square loss定义为L(y^ ,y)=(y^−y)2
，square loss定义为 L(y^ ,y)=max{0,1−y^y}。
目标函数就是一个更加宽泛的概念。目标函数是优化问题中的一个概念。任何一个优化问题包括两个部分：(1)目标函数，最终是要最大化或者最小化这个函数；(2)约束条件。约束条件是可选的，比如x<0x<0。
为了更生动形象的理解两者的区别，Prasoon Goyal举了三个例子。

• 既是损失函数又是目标函数
  最小二乘拟：给定一组的样本点{(x1,y1),…,(xn,yn)}{(x1,y1),…,(xn,yn)}，我们要求一条直线去拟合这些样本点。假设求出模型形式为y=βTxy=βTx。接着我们要最小化下面这个方程：
  
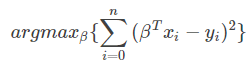
  上面的这个式子即使损失函数又是目标函数。所以在这个时候，损失函数和目标函数是同一个概念。

• 是目标函数但大于损失函数
  脊回归（Ridge regression）：类似于最小二乘拟合，不过脊回归假设参数足够简单。此时需要对ββ做正则化处理。需要优化的函数就变成：
  
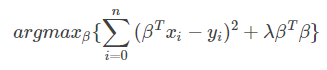
  上式可以称作是目标函数，但却不是损失函数。损失函数仅是这个函数的一部分。

• 是目标函数但没有损失函数
  极大似然估计：假设我们有一枚硬币，正面的概率是pp，方面的概率是(1−p)(1−p)。将这枚硬币抛了100次后，观察发现有42次正面向上，58次反面向上，求pp值？42次正面向上，58次反面向上的概率为p42(1−p)58p42(1−p)58。用极大似然发求pp则要优化下面的函数：
  
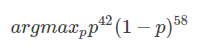
  在这个例子是仅有目标函数，不存在损失函数。