leetcode84.柱状图中最大的矩形(java)：单调栈

最新推荐文章于 2024-09-05 21:42:45 发布

原创最新推荐文章于 2024-09-05 21:42:45 发布 · 224 阅读

0 ·

CC 4.0 BY-SA版权

leetcode 专栏收录该内容

87 篇文章

订阅专栏

本文介绍了一种使用单调栈解决最大矩形面积问题的方法。通过维持一个单调递增的栈，当遇到非增元素时，计算并更新以栈顶元素为高的矩形的最大面积。最后遍历栈内剩余元素，确保所有可能的矩形面积都被计算。

题目
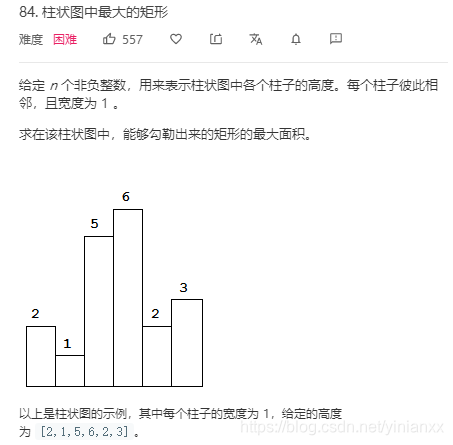
在这里插入图片描述
示例

思路
使用单调递增栈
比如[1,5,6]是递增的，那么此时栈内元素从栈顶开始是[3,2,1]，此时有三种构成矩形的可能，分别是6*(4-3)、5*(4-2)、1*(4-1)
由于是单调递增，右边比左边高，所以以左边值为高时，右边可以满足条件，所以矩形的宽为当前索引减去高的索引位置。（具体这个宽怎么算要具体看你怎么设置，但大概意思就是这样）
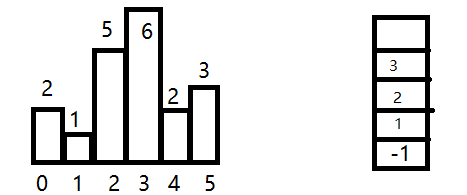
在这里插入图片描述
总结从左往右遍历，维持栈内索引对应的值是单调递增的。一旦遇到非增，逐个抛出栈顶元素，计算以该栈顶元素为高的矩形面积，更新最大值，直到栈底，然后将当前遍历到的索引入栈。

注意如果剩下的值一直在递增，就没办法计算这些矩形的面积，所以最后要遍历一次栈内元素，计算矩形面积，直到为空，或者只剩下哨兵，或者遍历完后，再设置一个哨兵0，这样就会在最后出现减元素。

具体代码

class Solution {
    public int largestRectangleArea(int[] heights) {
        Stack<Integer> stack = new Stack<>();
        stack.push(-1);
        int maxArea = 0;
        for(int i = 0;i < heights.length;i++){
            while(stack.peek()!=-1 && heights[stack.peek()]>heights[i]){
                maxArea = Math.max(maxArea,heights[stack.pop()]*(i - stack.peek()-1));
            }
            stack.push(i);
        }
        while(stack.peek() != -1){
            maxArea = Math.max(maxArea,heights[stack.pop()]*(heights.length - stack.peek()-1));
        }
        return maxArea;
    }
}