算法：贝尔曼-福特算法

最新推荐文章于 2025-02-13 19:52:05 发布

yimtcode

最新推荐文章于 2025-02-13 19:52:05 发布

阅读量887

点赞数

分类专栏：数据结构与算法文章标签：算法

本文链接：https://blog.youkuaiyun.com/yimtcode/article/details/121041613

版权

数据结构与算法专栏收录该内容

18 篇文章

订阅专栏

算法：贝尔曼-福特算法

1.简介

贝尔曼-福特算法（Bellman–Ford algorithm）是一个查找最短路径算法主要优点是支持负权重，但时间复杂度较高，还会有负权环的问题。
如果不需要权重应该使用广度优先或深度优先算法，如果只需要权重没有负权重，应该使用迪杰斯特拉算法，上面三种算法性能都会比贝尔曼-福特算法好很多。

2.图示

从A去D点路线，A->B->C->D

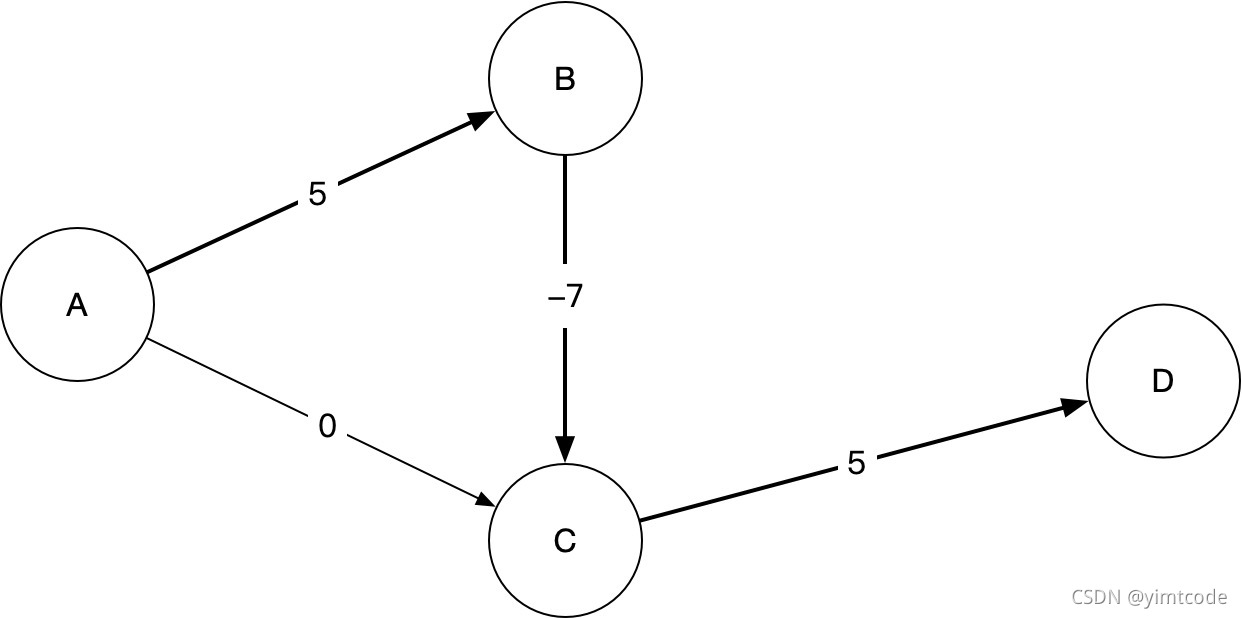
simple

负权环问题

正常情况下A->B->C->D的权重是3，是最近的一条路线。但是如果碰到下面这种情况就会出现回路问题，A->B->C->D时没有问题，下面还会一直D->B->C->D转圈，每转一圈权重就降1出现回路。算法最后需要检查是否出现回路。

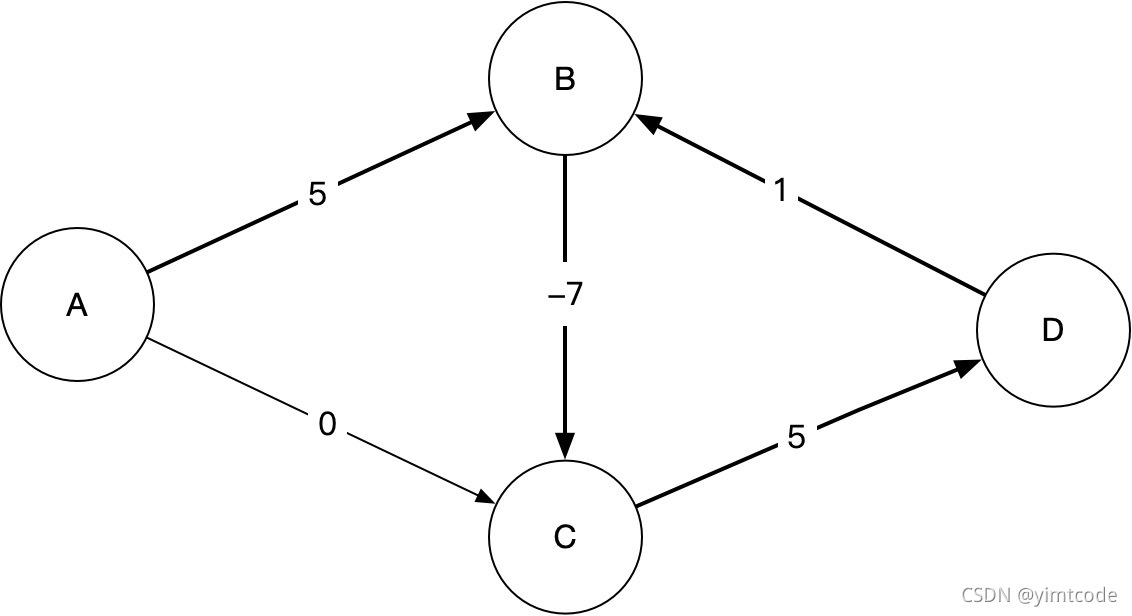
3.演示

package main

import (
	"fmt"
	"math"
)

func main() {
	graph := make(map[string]map[string]float32)
	graph["A"] = map[string]float32{
		"B": 5,
		"C": 0,
	}
	graph["B"] = map[string]float32{
		"C": -7,
	}
	graph["C"] = map[string]float32{
		"D": 5,
	}
	graph["D"] = map[string]float32{
	}
	distance, parent := bellmanFord(graph, "A")
	fmt.Println(distance)
	fmt.Println(parent)
}

func bellmanFord(graph map[string]map[string]float32, source string) (distance map[string]float32, parent map[string]string) {
	distance = make(map[string]float32)
	parent = make(map[string]string)
	// 添加当前点到所有节点权重
	// 权重为默认类型最大值
	for fromName := range graph {
		distance[fromName] = math.MaxFloat32
		parent[fromName] = ""
	}
	// 设置自身到自身的权重
	distance[source] = 0

	for i := 0; i < len(graph)-1; i++ {
		for fromName := range graph {
			for toName, weight := range graph[fromName] {
				currentWeight := distance[fromName] + weight
				if distance[toName] > currentWeight {
					// 记录最短距离 > 启始到父节点距离 + 父节点到当前子节点距离
					distance[toName] = currentWeight
					parent[toName] = fromName
				}
			}
		}
	}

	// 负权环检查
	for fromName := range graph {
		for toName := range graph[fromName] {
			if distance[toName] > distance[fromName] + graph[fromName][toName] {
				return nil, nil
			}
		}
	}
	return
}