题目描述
试题编号: 201412-2
试题名称: Z字形扫描
时间限制: 2.0s
内存限制: 256.0MB
问题描述
在图像编码的算法中,需要将一个给定的方形矩阵进行Z字形扫描(Zigzag Scan)。给定一个n×n的矩阵,Z字形扫描的过程如下图所示:
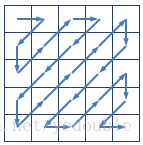
对于下面的4×4的矩阵,
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3
对其进行Z字形扫描后得到长度为16的序列:
1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3
请实现一个Z字形扫描的程序,给定一个n×n的矩阵,输出对这个矩阵进行Z字形扫描的结果。
输入格式
输入的第一行包含一个整数n,表示矩阵的大小。
输入的第二行到第n+1行每行包含n个正整数,由空格分隔,表示给定的矩阵。
输出格式
输出一行,包含n×n个整数,由空格分隔,表示输入的矩阵经过Z字形扫描后的结果。
样例输入
4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3
样例输出
1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3
评测用例规模与约定
1≤n≤500,矩阵元素为不超过1000的正整数。
第一种解法
解题思路
一、结合横坐标和纵坐标来看,z字形扫描是有规律的。
以4*4方阵为例:
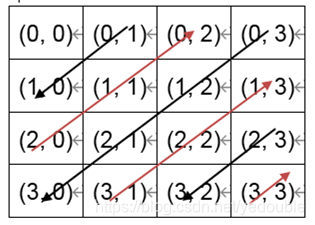
- 起点是(0, 0)位置。
- 斜向下扫描。经过的每一个单元格,横坐标+纵坐标=1。纵坐标从1,逐步减1,直至0。
- 斜向上扫描。经过的每一个单元格,横坐标+纵坐标=2。横坐标从2,逐步减1,直至0。
- 斜向下扫描。经过的每一个单元格,横坐标+纵坐标=3。纵坐标从3,逐步减1,直至0。
- 斜向上扫描。经过的每一个单元格,横坐标+纵坐标=4。横坐标从3,逐步减1,直至1。
- 斜向下扫描。经过的每一个单元格,横坐标+纵坐标=5。纵坐标从3,逐步减1,直至2。
- 斜向上扫描。经过的每一个单元格,横坐标+纵坐标=6。横坐标从3,逐步减1,直至3。(实际上只扫描一次)
二、进一步地,z字形扫描的规律可表述为:
(1)斜向下扫描时,纵坐标从min(t, n-1),逐步减1,直至t - min(t, n-1)。这里,t为该扫描线任意单元格横坐标加上纵坐标之和。min(t, n-1)是取t和n-1的最小值的意思。
(2)斜向上扫描时,横坐标从min(t, n-1),逐步减1,直至t - min(t, n-1)。这里,t为该扫描线任意单元格横坐标加上纵坐标之和。
(3)t为奇数,是斜向下扫描。t为偶数,是斜向上扫描。
参考答案
n = int(input())
n_mtx = []
for i in range(n):
n_line = [int(s) for s in input().split()]
n_mtx.append(n_line)
# print(n_mtx)
print(n_mtx[0][0], end = ' ')
max_xplusy = n - 1 + n - 1 #横坐标+纵坐标之和的最大值,即右下角元素的横坐标+纵坐标之和
#沿斜线迭代n*n方阵mtx的元素,这些元素的横坐标+纵坐标=t
def itr(mtx, n, t):
start = min(n-1, t)
if t % 2 == 0: #偶数,斜向上遍历
for x in range(start, t - start - 1, -1):
print(mtx[x][t-x], end = ' ')
else: #t为奇数,斜向下遍历
for y in range(start, t - start - 1, -1):
print(mtx[t-y][y], end = ' ')
for t in range(1, max_xplusy + 1):
#遍历斜线上的元素
itr(n_mtx, n, t)
第二种解法
第二种解法费劲些,是我以前编写的。我保留该解法以供对比。你可以看到,第一种解法的思路更清晰,代码更简洁,引发错误的环节更少。
解题思路
- 扫描从左上角出发,首先是右拐,接下来扫描的顺序是: 沿左下移动 --> 拐弯 --> 沿右上移动 --> 拐弯 --> 沿左下移动 -->… (不断重复)。什么时候要拐弯?答案是当移动到矩阵边界的时候。
- 拐弯有两种,一是向右,二是向下。什么时候向右?答案是移动到矩阵顶部或底部的时候。什么时候向下?答案是移动到矩阵左边界或右边界的时候。特别注意,移动到右上角元素的时候,要向下拐弯。移动到左下角元素的时候,要向右拐弯。
参考答案
def turn(row, column, n_size):
'''拐弯的处理'''
if row == n_size - 1: #已到达底部
column += 1
elif column == n_size - 1: #已到达右边界
row += 1
elif row == 0: #已到达顶部(须放在‘已到达右边界’之后)
column += 1
elif column == 0: #已到达左边界(须放在‘已到达底部’之后)
row += 1
return (row, column)
def move_left_down(row, column, n_size):
'''向左下移动一格。到达边界的话,则拐弯。'''
if column == 0 or row == n_size - 1:
row, column = turn(row, column, n_size)
return (row, column, 1)
else:
row += 1
column -= 1
return (row, column, 0)
def move_right_up(row, column, n_size):
'''向左上移动一格。到达边界的话,则拐弯。'''
if row == 0 or column == n_size - 1:
row, column = turn(row, column, n_size)
return (row, column, 0)
else:
row -= 1
column += 1
return (row, column, 1)
#输入矩阵
n = int(input())
n_mtx = []
for i in range(n):
n_line = [int(s) for s in input().split()]
n_mtx.append(n_line)
# print(n_mtx)
#打印左上角元素
print(n_mtx[0][0], end = ' ')
row = 0
column = 1
move_index = 0 #0: left_down, 1: right_up。
#依次打印扫描到的元素
while row < n and column < n:
print(n_mtx[row][column], end = ' ')
if move_index == 0: #0与1交替,决定了扫描移动的方向
row, column, move_index = move_left_down(row, column, n)
else:
row, column, move_index = move_right_up(row, column, n)
代码有些长,有没有更加简洁的思路。如果读者找到更加简洁的思路,请在留言中指出。
测试用例
- n为偶数的情形。比如4x4的矩阵。题目描述给出的测试用例覆盖了本情形。
- n为奇数的情形。比如5x5的矩阵。
样例输入
3
1 2 6
3 5 7
4 8 9
样例输出
1 2 3 4 5 6 7 8 9 - n为1的情形。不要忘了这种极端情形。
样例输入
1
5
样例输出
5
小结
- 第一种解法的代码明显比第二种解法的代码短。在编程的时候,尽量找到简洁的算法。
- 本题,n为1的情形是一个坑。






 本文详细解析了CCFCSP竞赛中Z字形扫描题目的两种解法,第一种解法利用横纵坐标规律简洁高效,第二种解法通过边界判断实现扫描,附带代码示例及测试用例。
本文详细解析了CCFCSP竞赛中Z字形扫描题目的两种解法,第一种解法利用横纵坐标规律简洁高效,第二种解法通过边界判断实现扫描,附带代码示例及测试用例。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








