决策树

预备知识

1.熵 ：表示随机变量不确定性的度量。

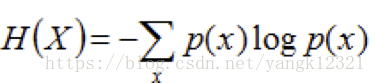
2.条件熵：表示在已知随机变量X的条件下随机变量Y的不确定性。

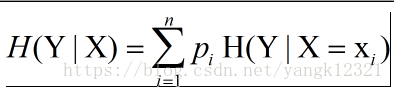
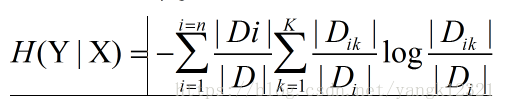
3.信息增益 ：特征A对训练数据集D的信息增益g(D,A),定义为集合D的熵(经验熵)与特征A给定条件下D的条件熵(经验条件熵)H(D|A)之差，即

 g(D,A)=H(D)-H(D|A)

信息增益越大越好，越大说明经过A特征数据的不确定性越小。但是信息增益存在偏向于选择取值较多的特征的问题。

4.信息增益比 ：特征A对训练数据集D的信息增益g(D,A)与训练数据集D关于特征A的值的熵H(D)之比，即

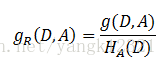
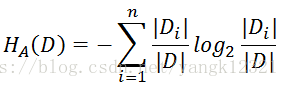
决策树分为三部分：1) 特征选择  2）决策树生成  3）决策树剪枝

ID3算法中的一些知识，输入：训练集，特征集，阈值

1.输入数据为同一类

2.无特征 3.设置信息增益阈值 

C4.5 与DI3不同在于特征选取的时候将信息增益换成信息增益比。

决策树的剪枝

剪枝是通过极小化决策树整体的损失函数，或者代价函数来实现的。设树T的结点个数为|T|，t是树T的叶结点，该叶结点有N个样本，其中k类的样本点有N(k)个，H(T)为叶结点t上的经验熵。决策树的损失函数可以定义为

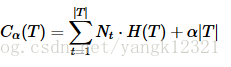
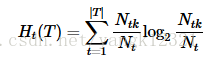
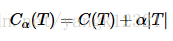
剪枝算法

输入：生成算法产生的整个数，与参数α

输出：修剪后的子树

(1) 计算每个结点的经验熵

(2) 递归地从树的叶结点向上回缩

    设一组叶结点回缩到父结点之前与之后的整体树分别为T1与T2，对应损失函数值分别是C1(T1)与C1(T2)，如果C1(T1)<=C1(T2),则进行剪枝，即将父结点做为新的叶结点。

(3) 返回(2)，直至不能继续为止，等到损失函数最小的子树。

CART决策树：假设决策树是二叉树，内部结点特征的取值为‘是’与‘否’，左分支取‘是’，右分支取‘否’。

1.预备知识：

最小二乘法：

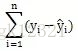
基尼指数 ：在分类问题中，假设有K个类，样本点属于第K类的概率为Pk，则概率分布的基尼指数定义为：

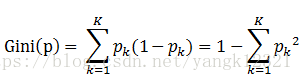
对于给定的样本集合D，其基尼指数为：

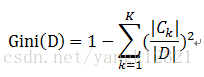
其中Ck是D中属于第k类的样本子集，K是类别个数。

在样本集合D根据特征A是否取某一个可能值a被分割成D1与D2两个部分，即

D1={(x,y)∈D|A(x)=a},   D2=D-D1

在特征A条件下，集合D的基尼指数定义为：

Gini(D,A)=(D1/D)Gini(D1)+(D2/D)Gini(D2)

基尼指数表示集合D的不确定性，基尼指数Gini(D,A)表示经A=a分割后，集合D的不确定性。

2.CART生成

回归树的生成

回归树用平方误差最小化准则进行特征选择，生成二叉树。

假设X与Y分别为输入和输出变量，且Y是连续变量，给定训练数据集

    D={(x1,y1),(x2,y2),.................,(x1,y1)}

输出Y为连续变量，将输入划分为M个区域，分别为R₁,R₂,…,R_M,每个区域的输出值分别为：c1,c2,…,c_m则回归树模型可表示为：

在单元Rm上的Cm的最优值Cm1是Rm上所有实例x的y的值的平均。Cm1=ave(y1|x1∈Rm)

则平方误差为：

假如使用特征j的取值s来将输入空间划分为两个区域，分别为：

我们需要最小化损失函数，即：

　　其中c1,c2分别为R1,R2区间内的输出平均值。（此处与统计学习课本上的公式有所不同，在课本中里面的c1,c2都需要取最小值，但是，在确定的区间中，当c1,c2取区间输出值的平均值时其平方会达到最小，为简单起见，故而在此直接使用区间的输出均值。

最小二乘法回归树生成算法

输入：训练数据集

输出：回归树

在训练数据集所在的输入空间中，递归地将每个区域划分为两个子区域并决定每个子区域的输出值，构建二叉决策树。

(1)选择最优切分变量j与切分点s，求解

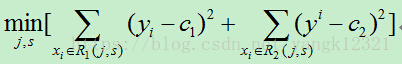
遍历所有的j，对固定的切分变量j扫描切分点s，求出最小值的对(j,s)

(2) 用选定的对(j,s)划分区域并决定相应的输出值：

Cm1=ave(y1|x1∈Rm)

(3)继续对两个子区域调用步骤1,2，指导满足停止条件。

(4)将输入空间划分成M个区域，生成决策树:

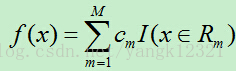
分类树的生成

输入：训练数据集D，停止计算条件；

输出：CART决策树

(1) 对每个特征的每个值算基尼指数，找出最优特征以及最优特征点。

(2) 对两个子结点递归的调用步骤1，直至满足停止条件。

(3) 生成决策树。