将多边形实体进行旋正_js 将多边形旋转正-优快云博客

博客介绍了几何实体按“最长边”旋转的操作。直接按多边形最长边旋转可能得不到预期结果，需先移除共线点来计算最长边。给出了移除共线点的方法及代码，还展示了计算旋转角度的代码，算出角度后即可对实体进行旋转。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在进行几何实体操作时，有时候是需要将实体安装”最长边“进行旋转，例如：

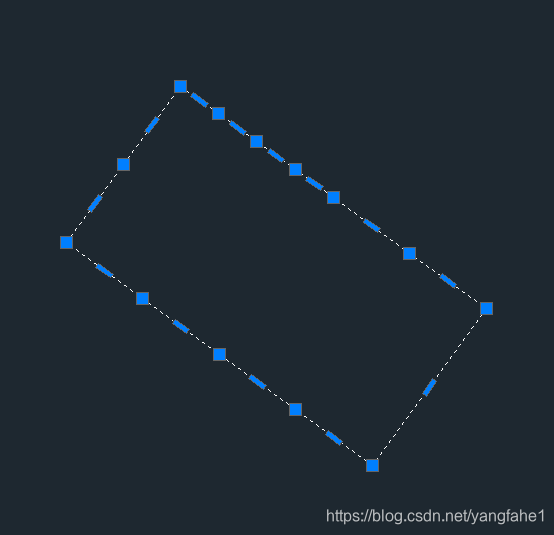
从第一个图中可以看出，实体最长的边是有很多个节点，如果我们直接安照多边形中最长的边进行旋转那么最终的结果是下图这样的：

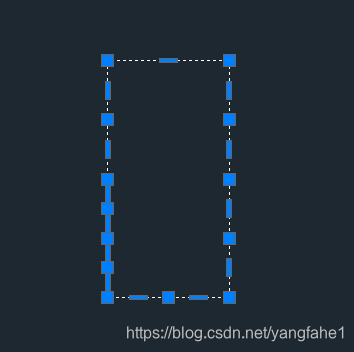
这样就不是我们想要的结果，所以在计算旋转角度的时候，我们需要先将一些共线的点给忽略掉，这样我们就可以计算出最长的边。

移除共线的点方法：

//点与线的位置关系

enum PointLocation
{
   Line_Left,
   Line_Right,
   Collinear_Left,
   Collinear_Right,
   Collinear_Contain
};

PointLocation collinearTest(const Point &P, const Point &Q1, const Point &Q2)
{
Vector A = Vector(P.x - Q1.x, P.y - Q1.y);
Vector D = Vector(Q2.x - Q1.x, Q2.y - Q1.y);
Vector N = -D.perpVector();
   double val = N.dotProduct(A);
   if(val > 0) return Line_Left;
   else if(val < 0) return Line_Right;
   val = D.dotProduct(A);
   if(val < 0) return Collinear_Left;
   else if(val > D.dotProduct(D)) return Collinear_Right;
   return Collinear_Contain;
}

PointArray removeSurplusPoint(const PointArray &node)
{
   int len = node.length(); PointArray node1;
   for(int idx = 1; idx < node.length(); ++idx)
   {
Point p1 = node[(idx - 1) % len];
Point p2 = node[(idx + 0) % len];
Point p3 = node[(idx + 1) % len];
       if(Collinear_Contain == collinearTest(p2, p1, p3)) continue;
       node1.append(p2);
   }
   return node1;
}

//计算旋转角度
double rotateAngle(const PointArray &node)
{
   double ang= 0.0, dist = 0.0;
   int len = node.length();
   for(int idx = 0; idx < len; ++idx)
   {
Point spt = node[idx];
Point ept = node[(idx + 1) % len];
       double temp = spt.distance(ept);
       if(temp > dist) { dist = temp; ang= angle(spt, ept); }
   }
   return -ang;
}

计算出旋转角度之后，我们就可以对实体进行旋转。旋转的结果就是第二个图。