算法思想
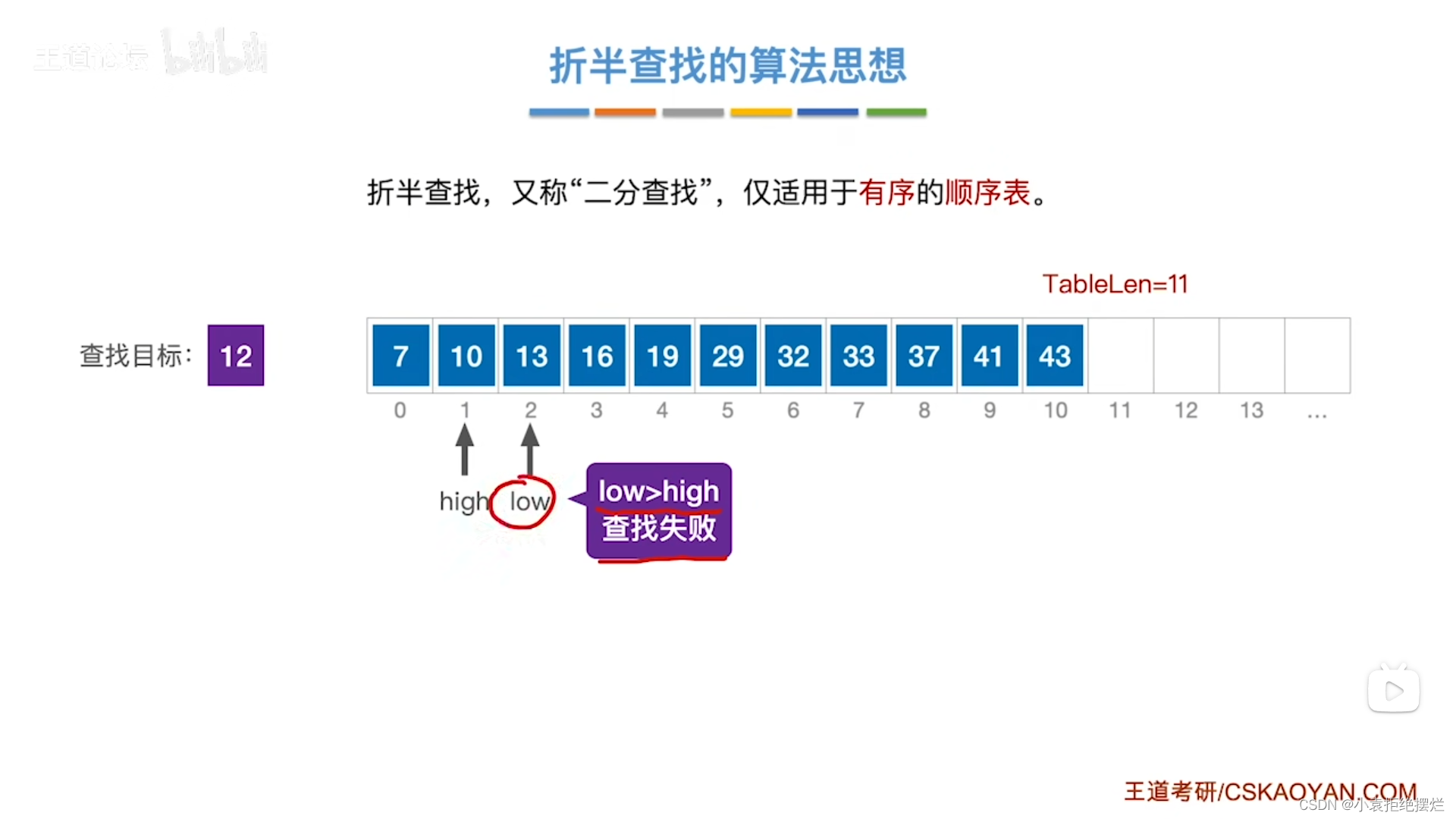
首先折半查找又称二分查找只针对于有序顺序表
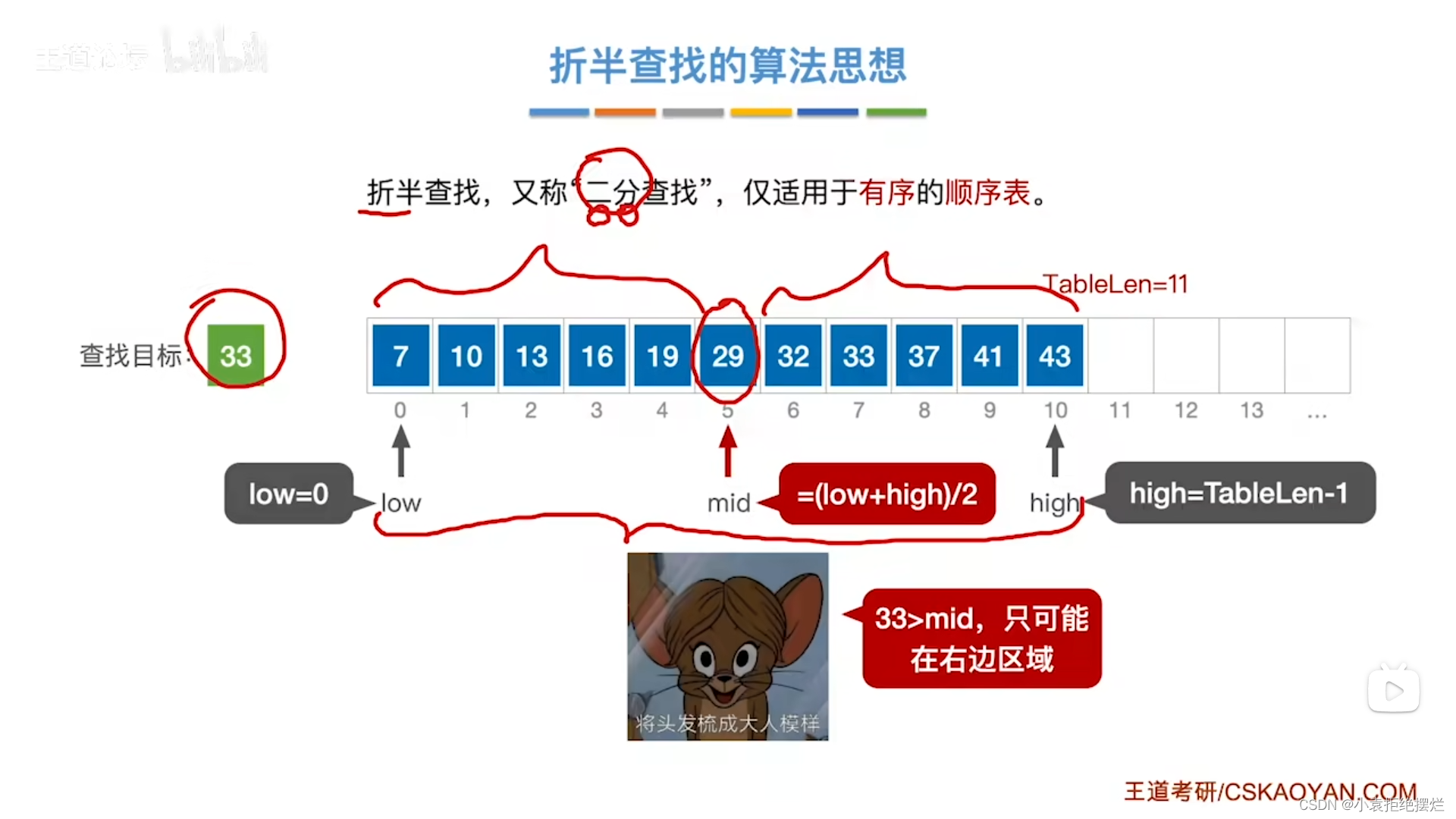
重要思想就是对半分
把0号位置给一个low
然后顺序表的最高位赋一个high位
然后使
middle=low+high/2
然后比较
data[middle]与我们要找的数据的对应大小,大的话就是在middle的右边
小的话就是在middle的左边
(如果等于的话就查找的就是middle)
如果大于middle把low=middle+1
如果小于就是high=middle-1
重点-查找数据只能出现在[low,high]之间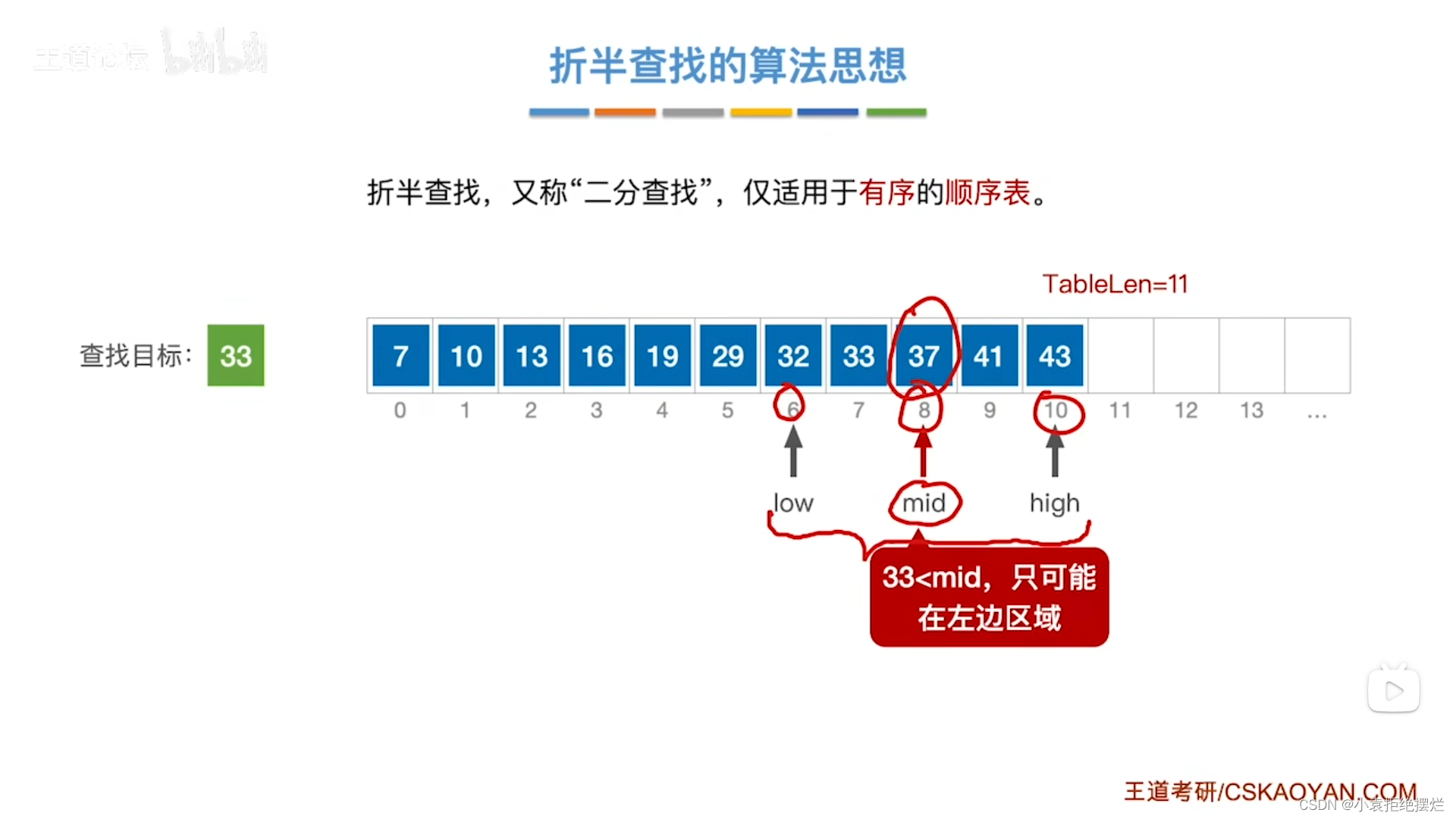
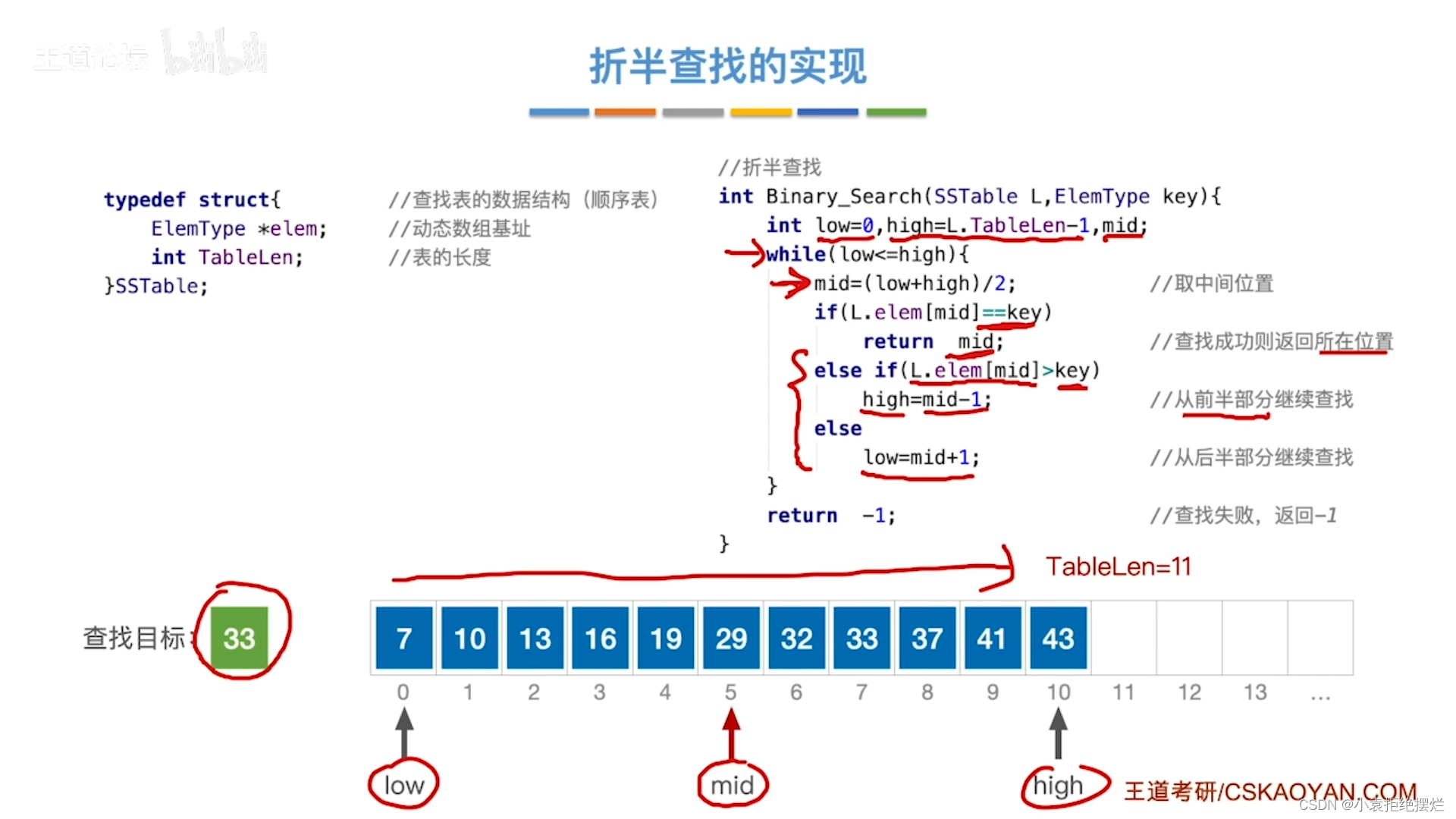
比如图中我们找的是33
此时33<37
high=mid-1
high=7
data[high]=33
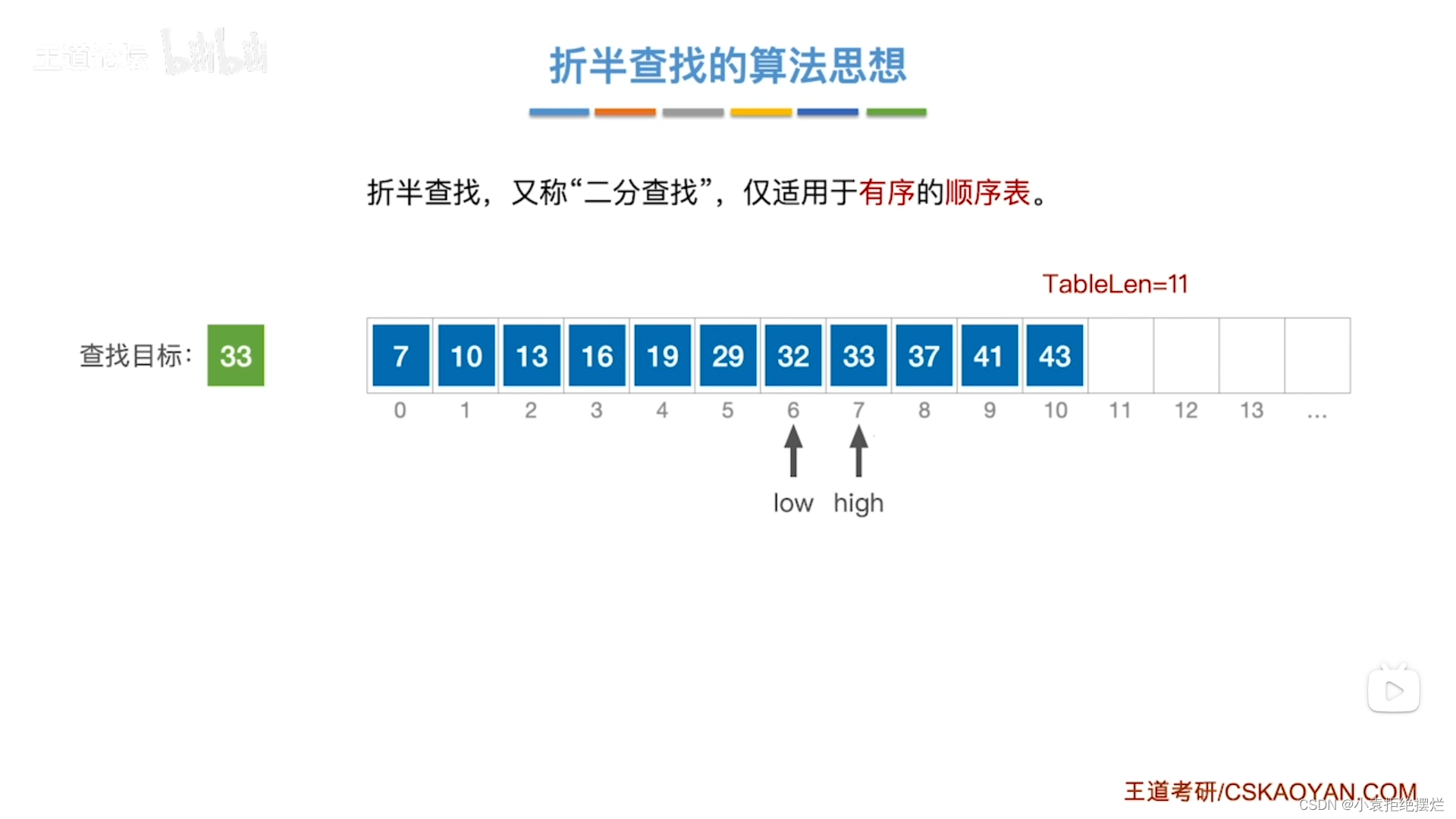
然后mid=(6+7)/2=6
data[mid]=32
low=mid+1=7
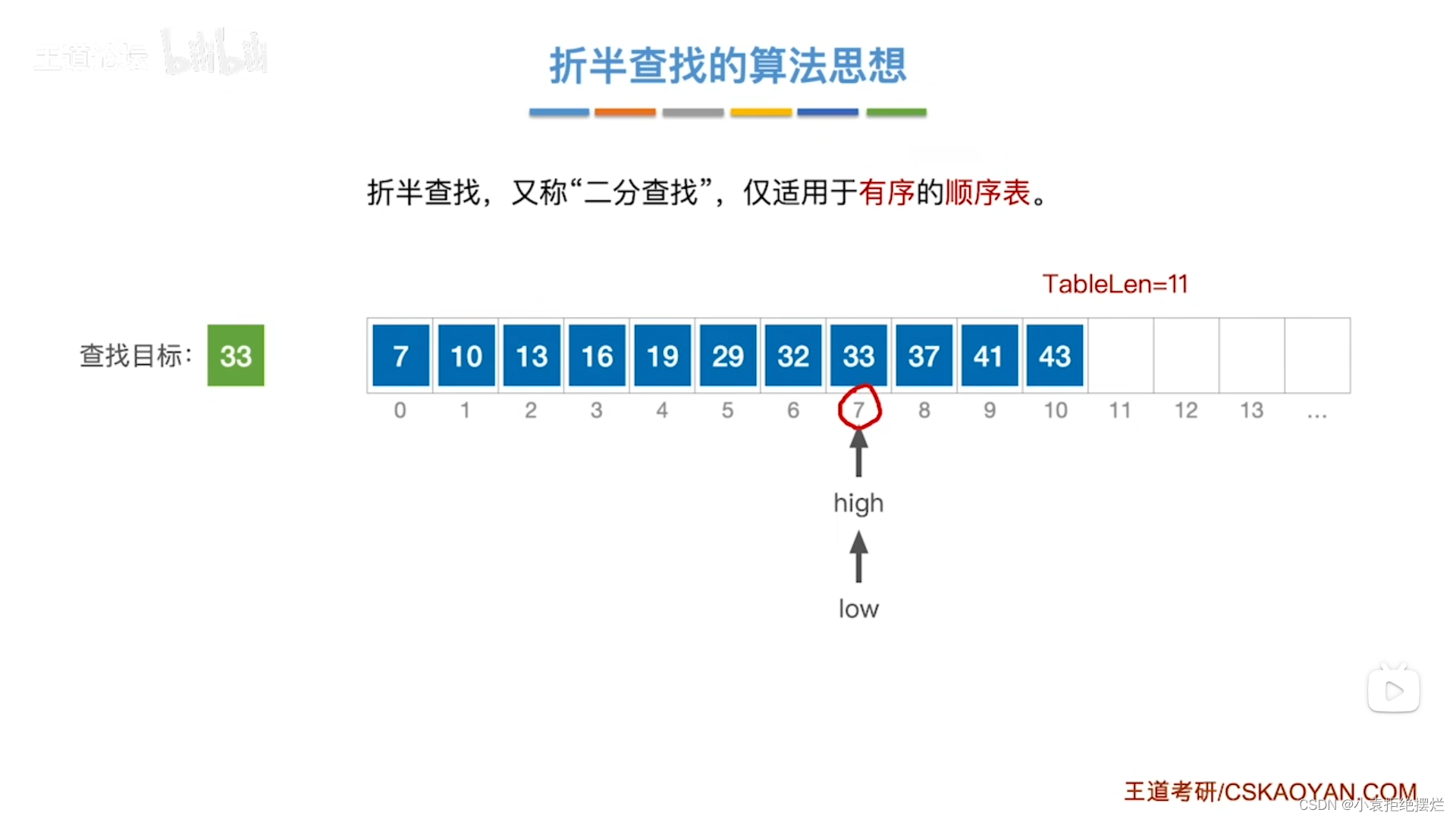
现在low和high指向同一个元素
mid=(low+high)/2=7
然后
data[mid]=33查找成功
如果这个不算33是34比如
那么high=mid-1
这样的话high=6 low=7
循环条件失效,查找失败
算法实现
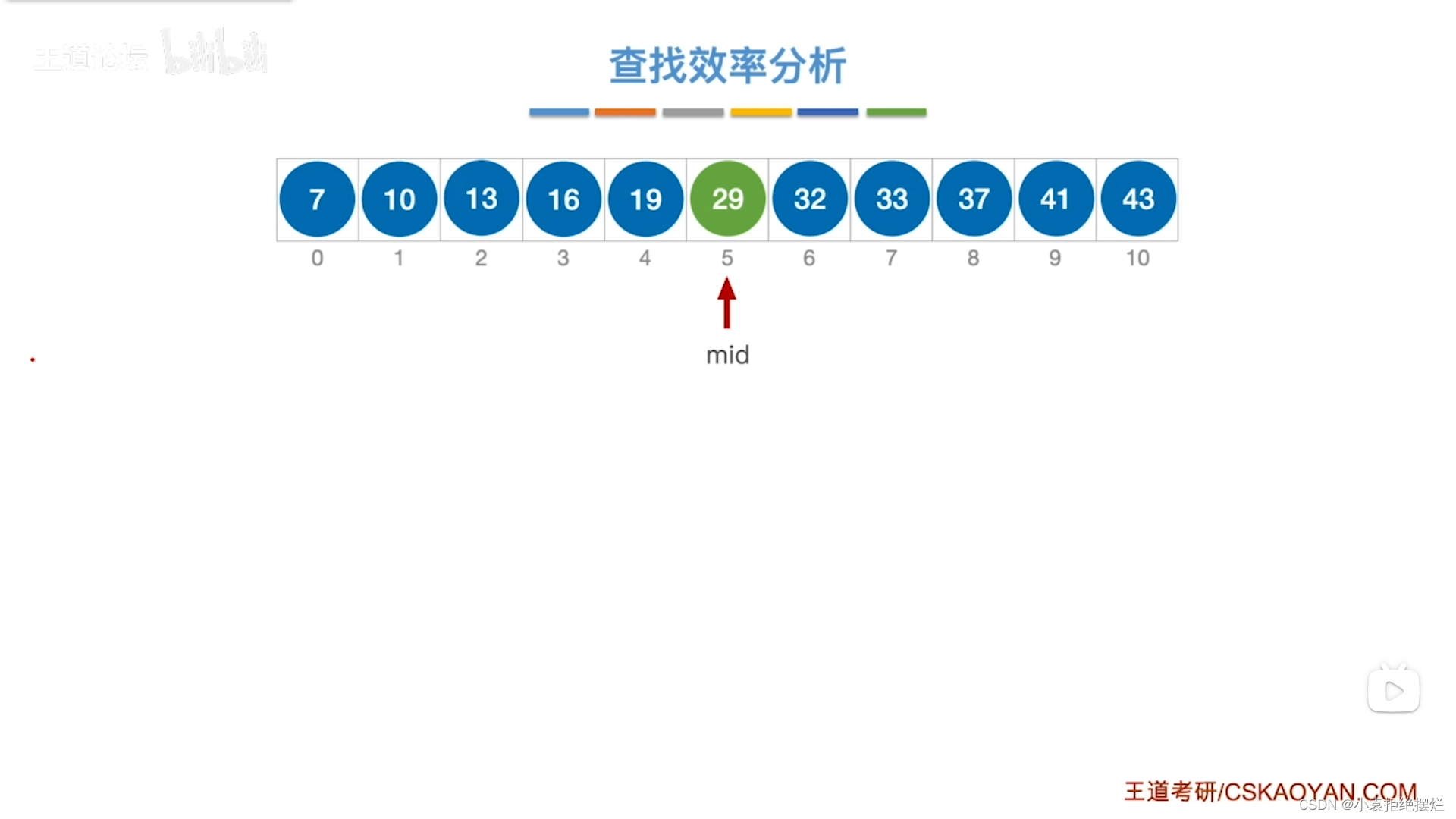
查找效率分析
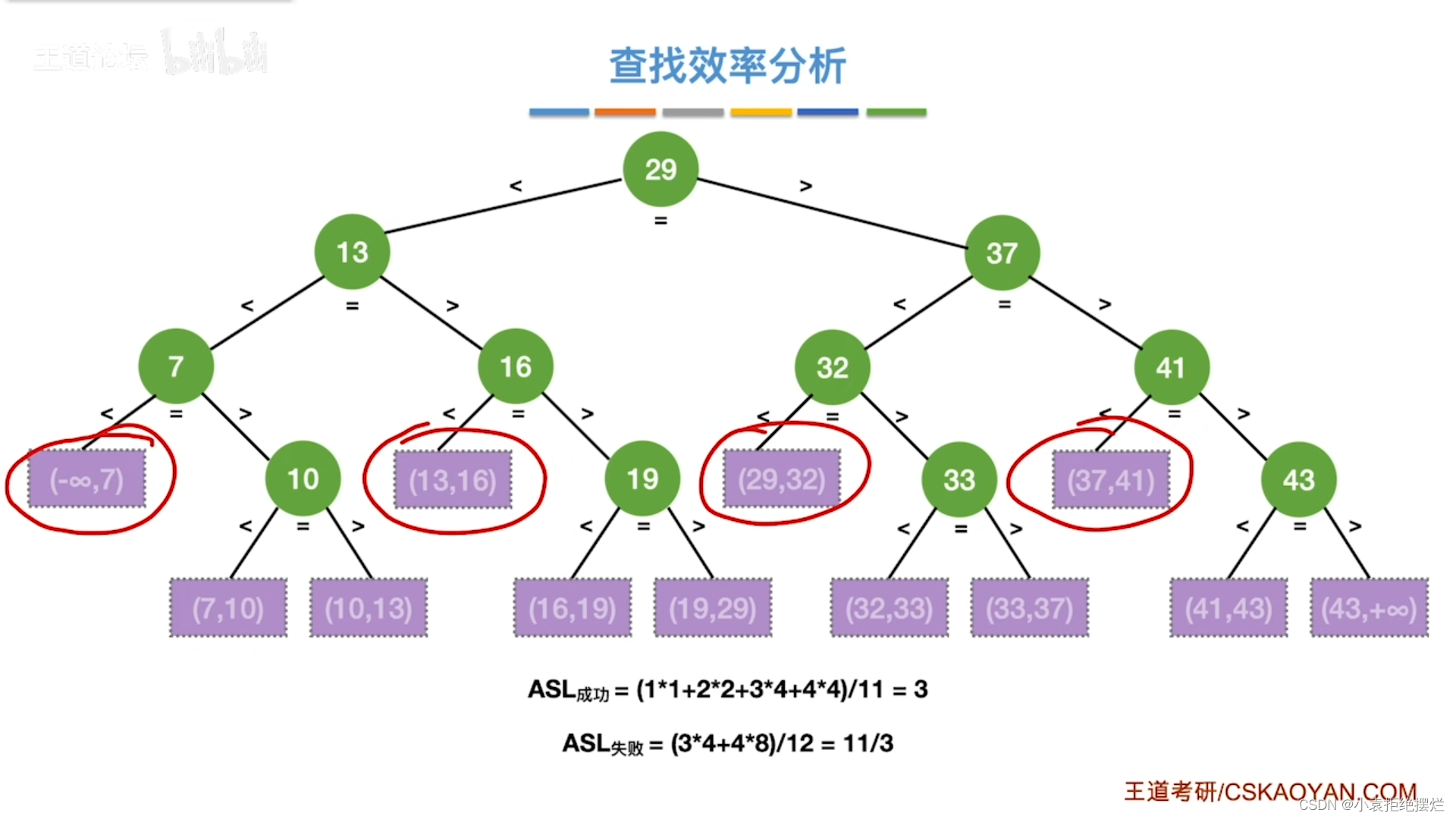
查找判定树的构造
奇数个元素
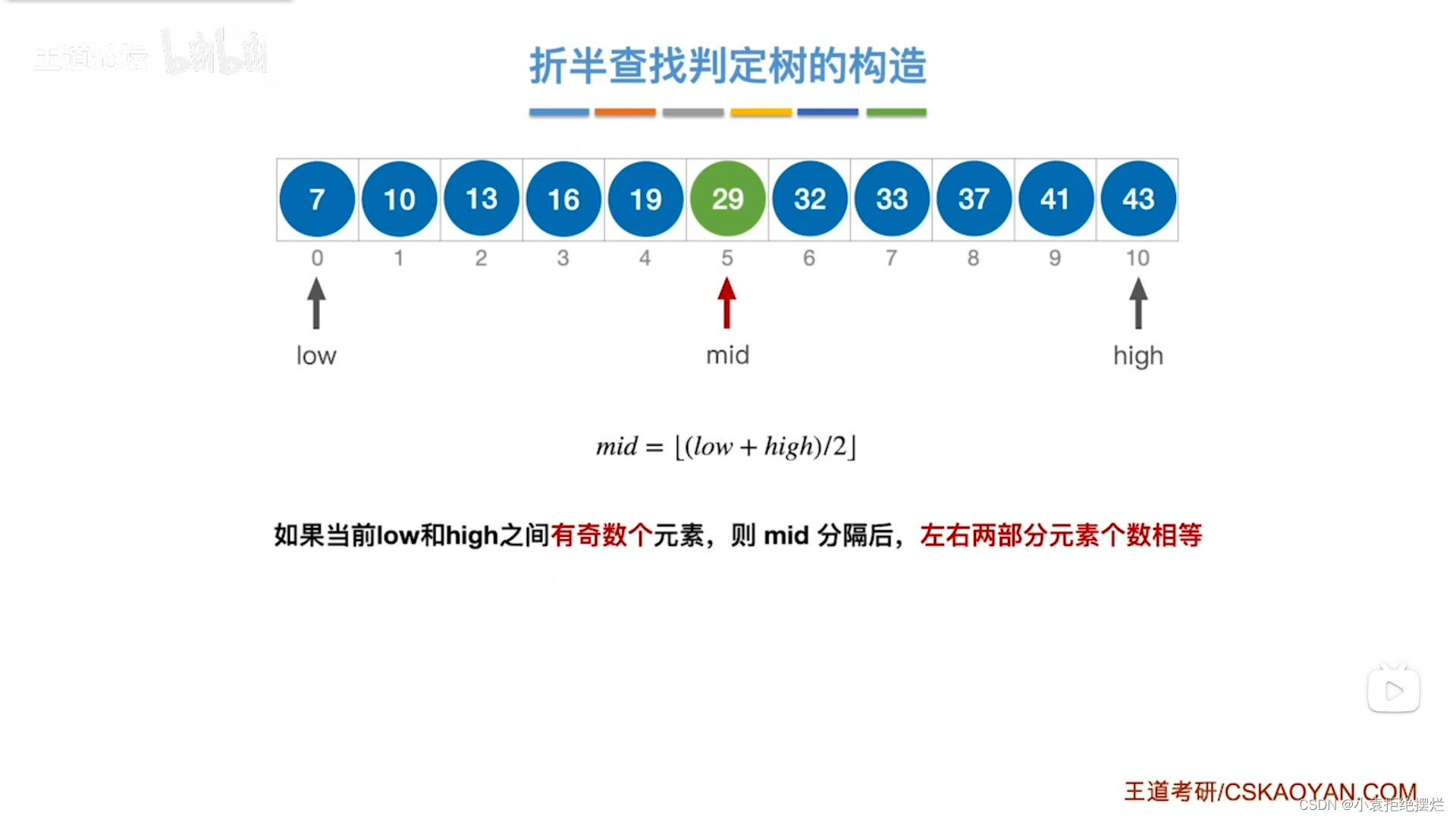
当元素的个数奇数个时
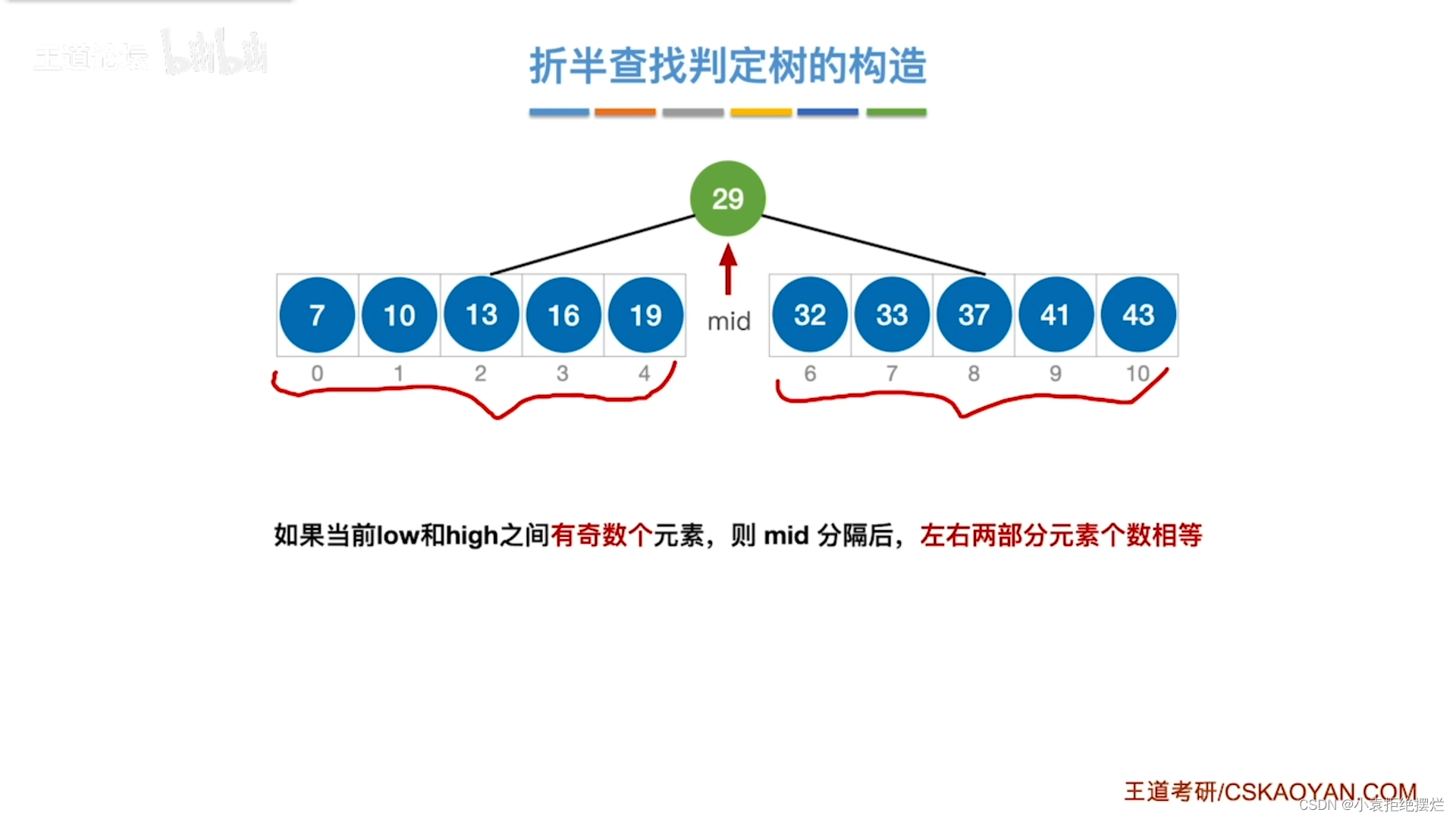
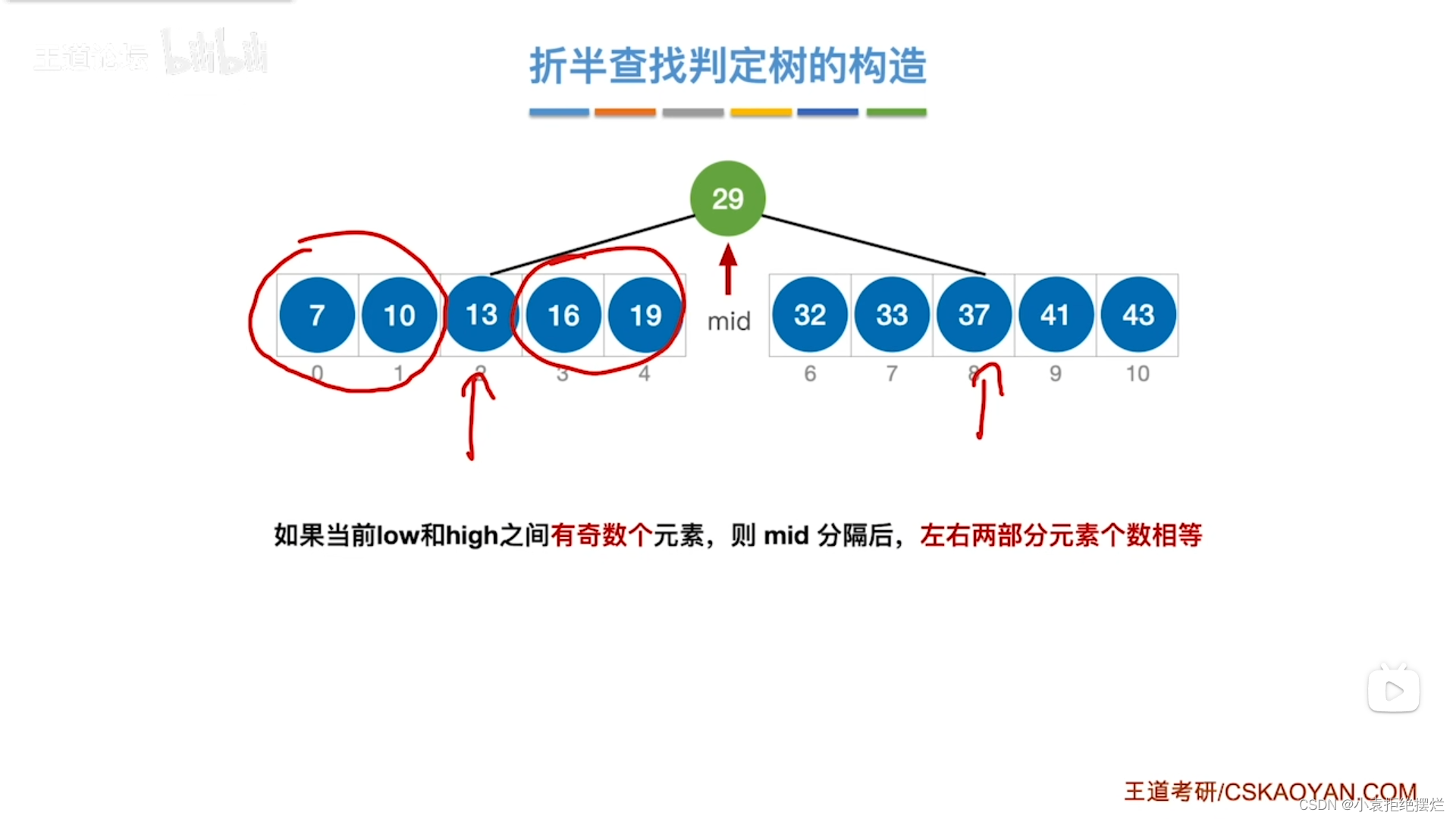
然后在找中间的可以一步步切割
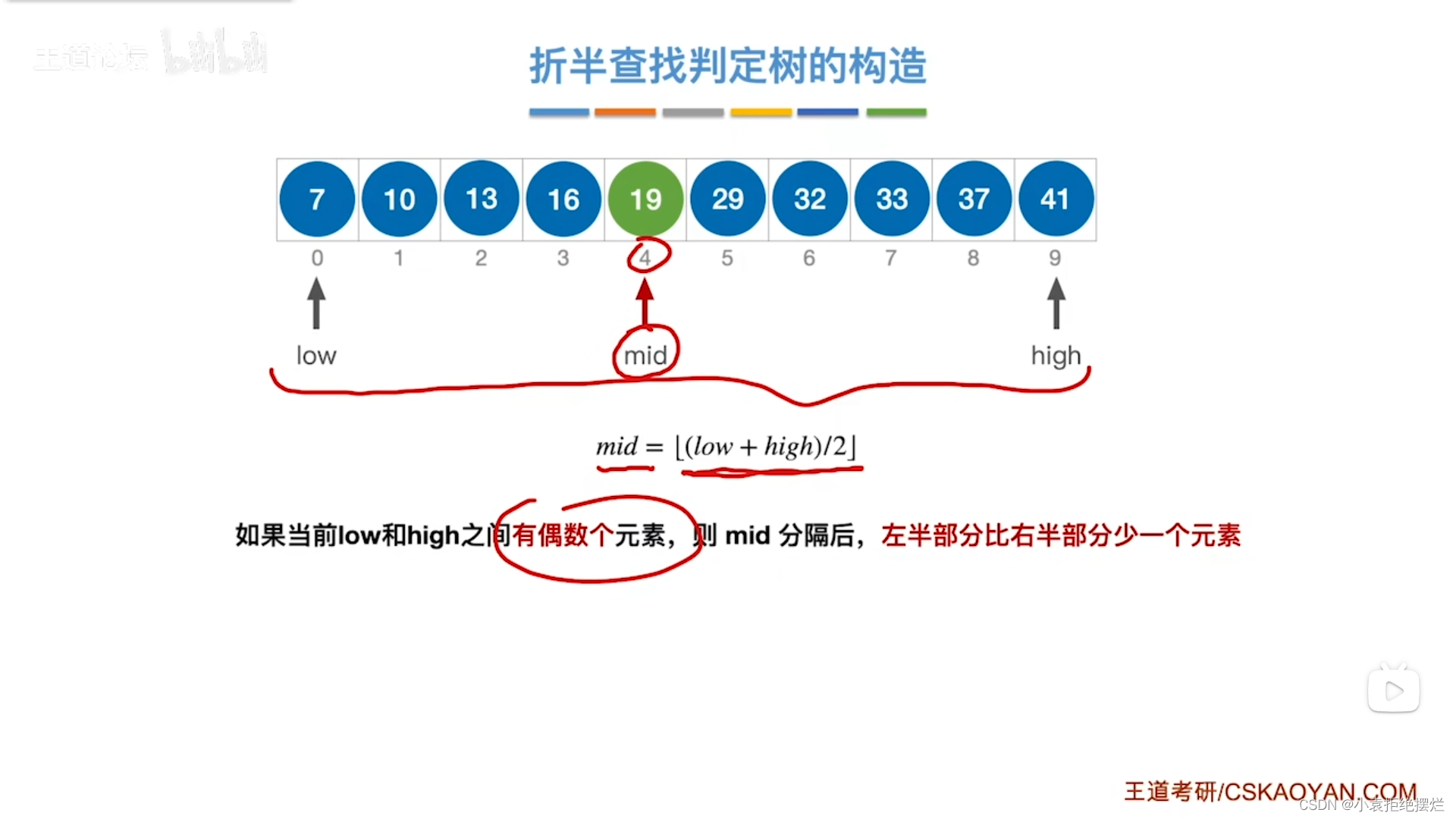
偶数个元素
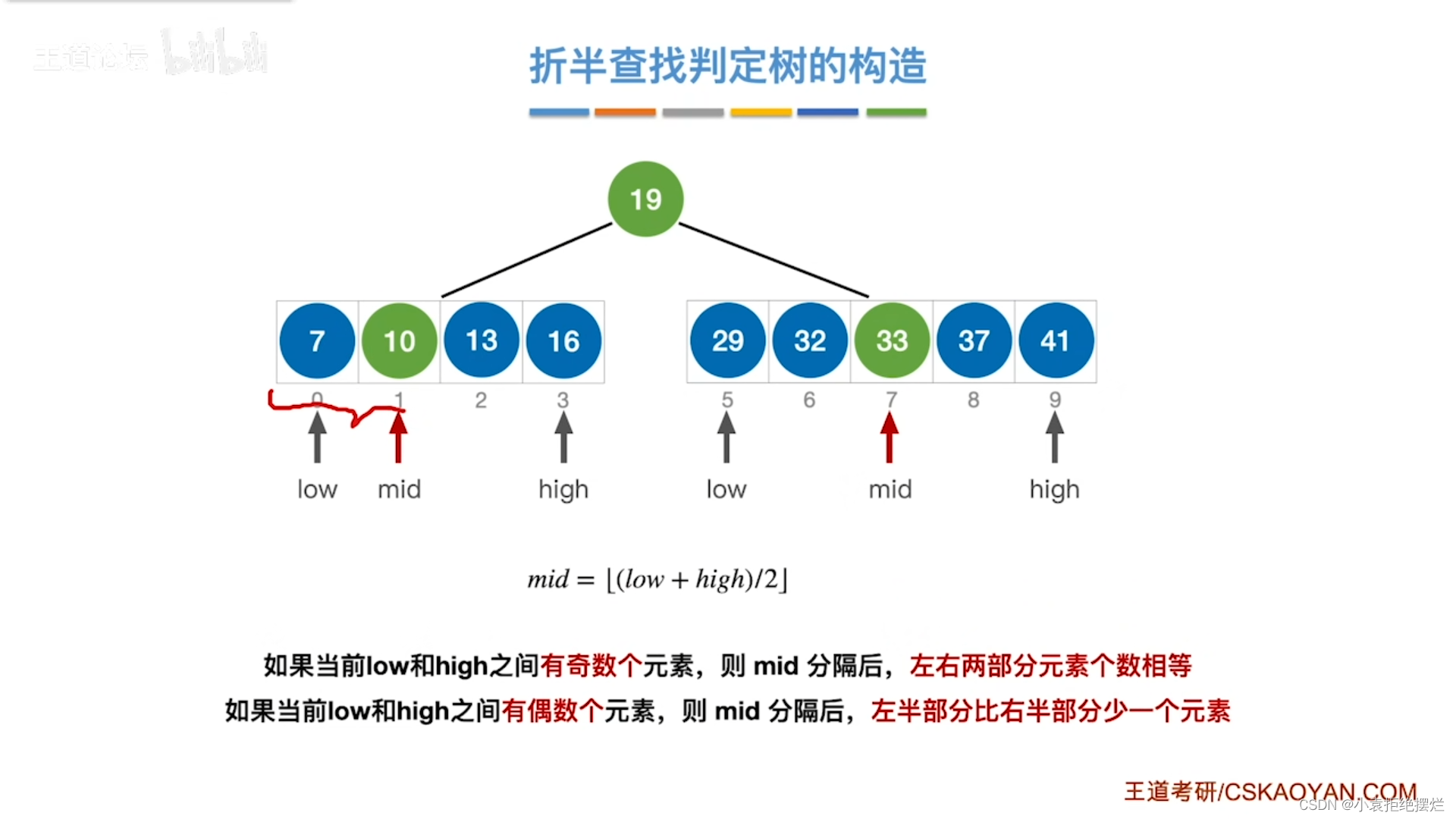
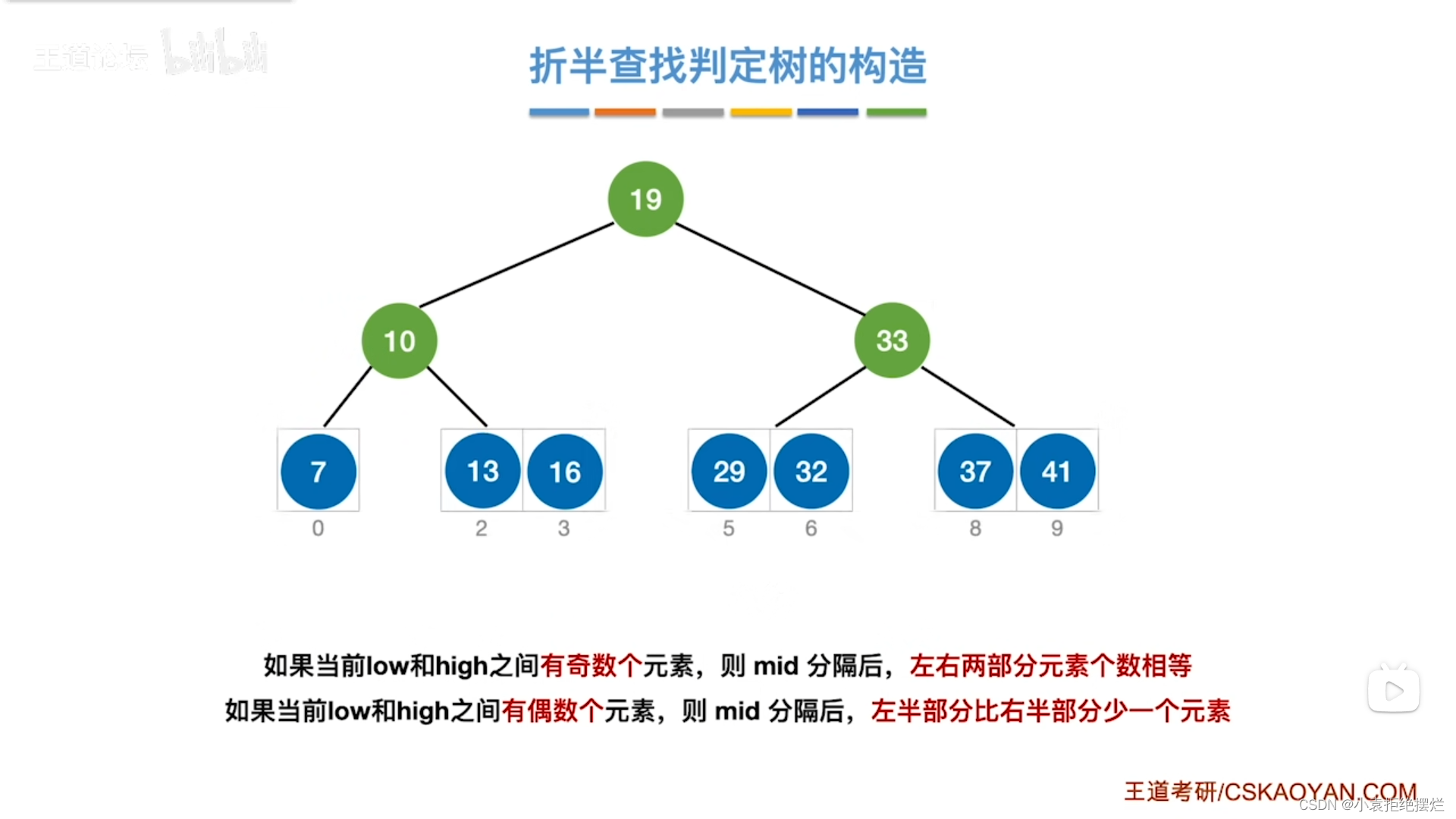
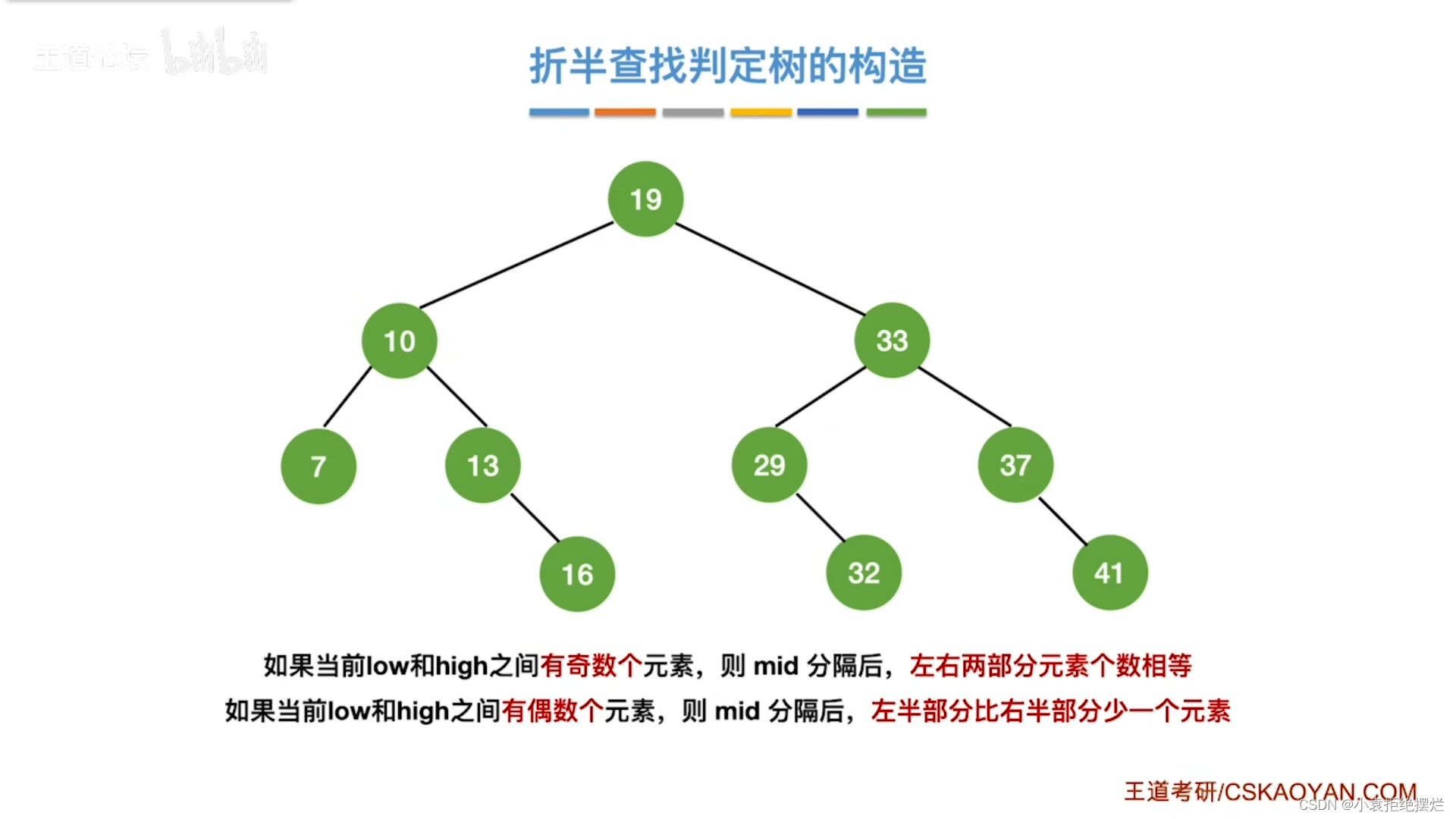
结论

右子树的节点要么比左子树节点多一个,要么和左子树相等
对应练习
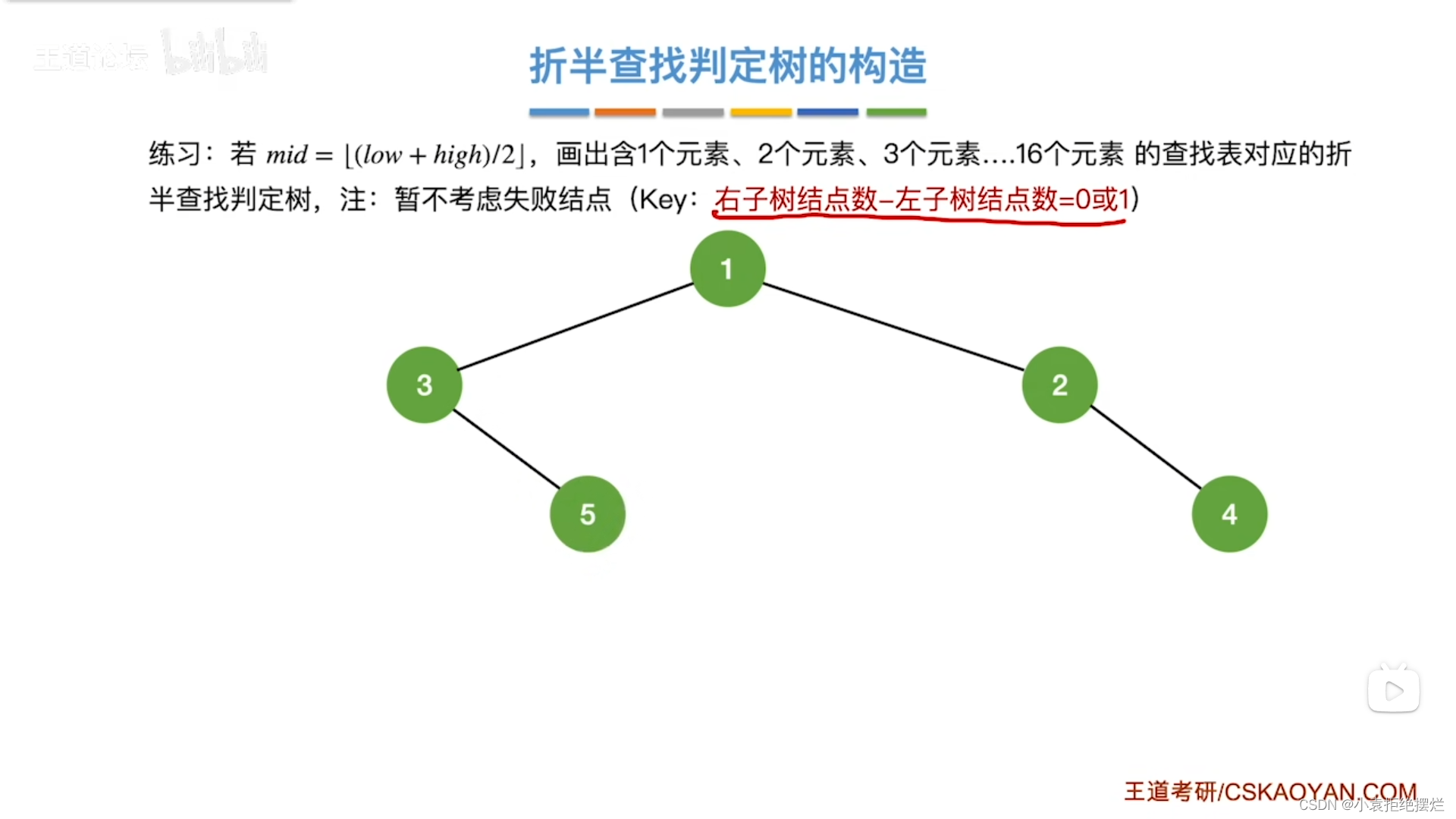
就是总是先加到右子树上面
然后加到左子树上面,且要一级一级考虑
(就是加完4以后加1的左子树呗,就是3,3肯定也要加到右子树上呗就加个5节点
这就叫一级一级考虑)
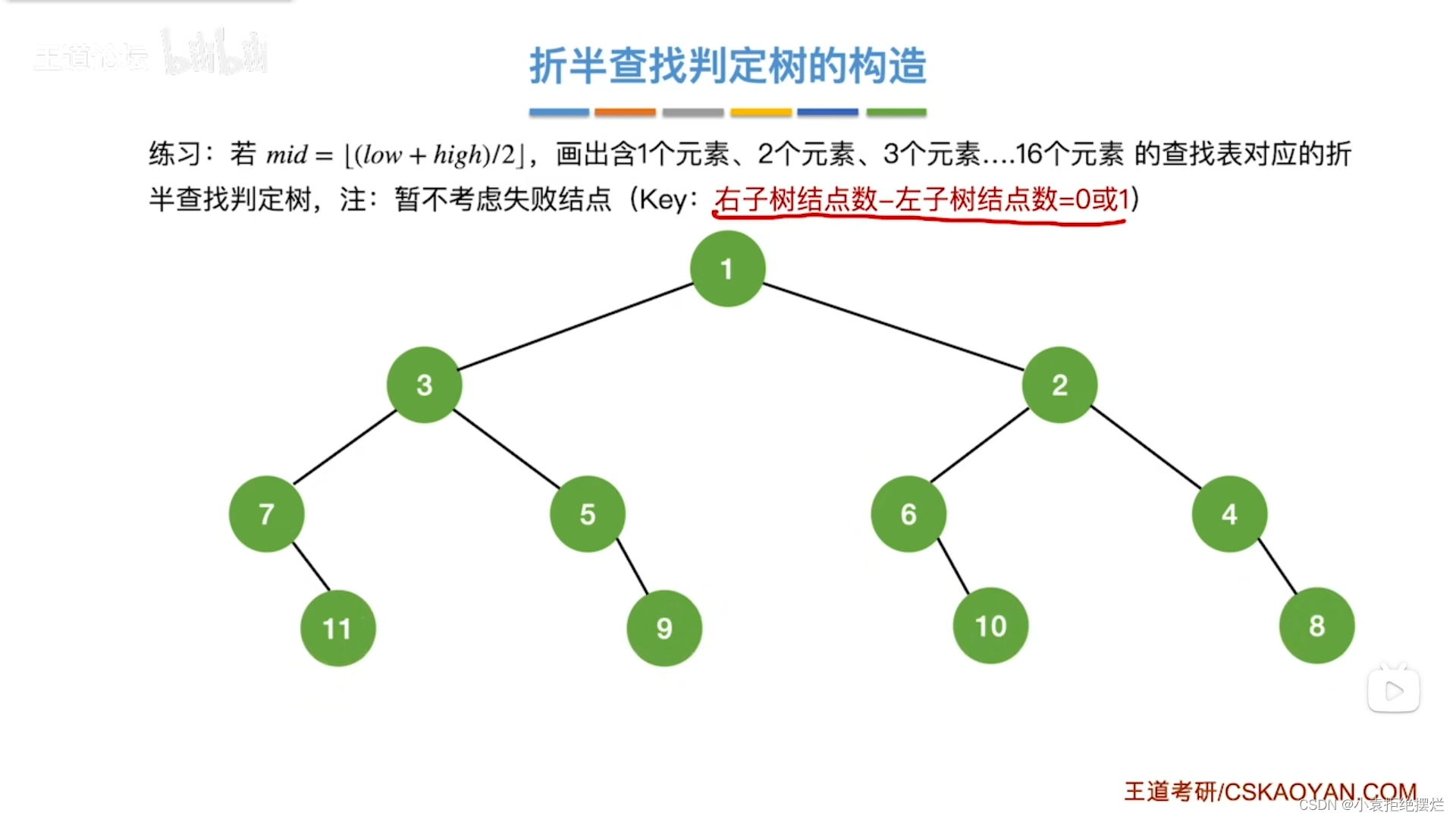
这个折半查找判定树平衡二叉树呗
那就有个对应的性质
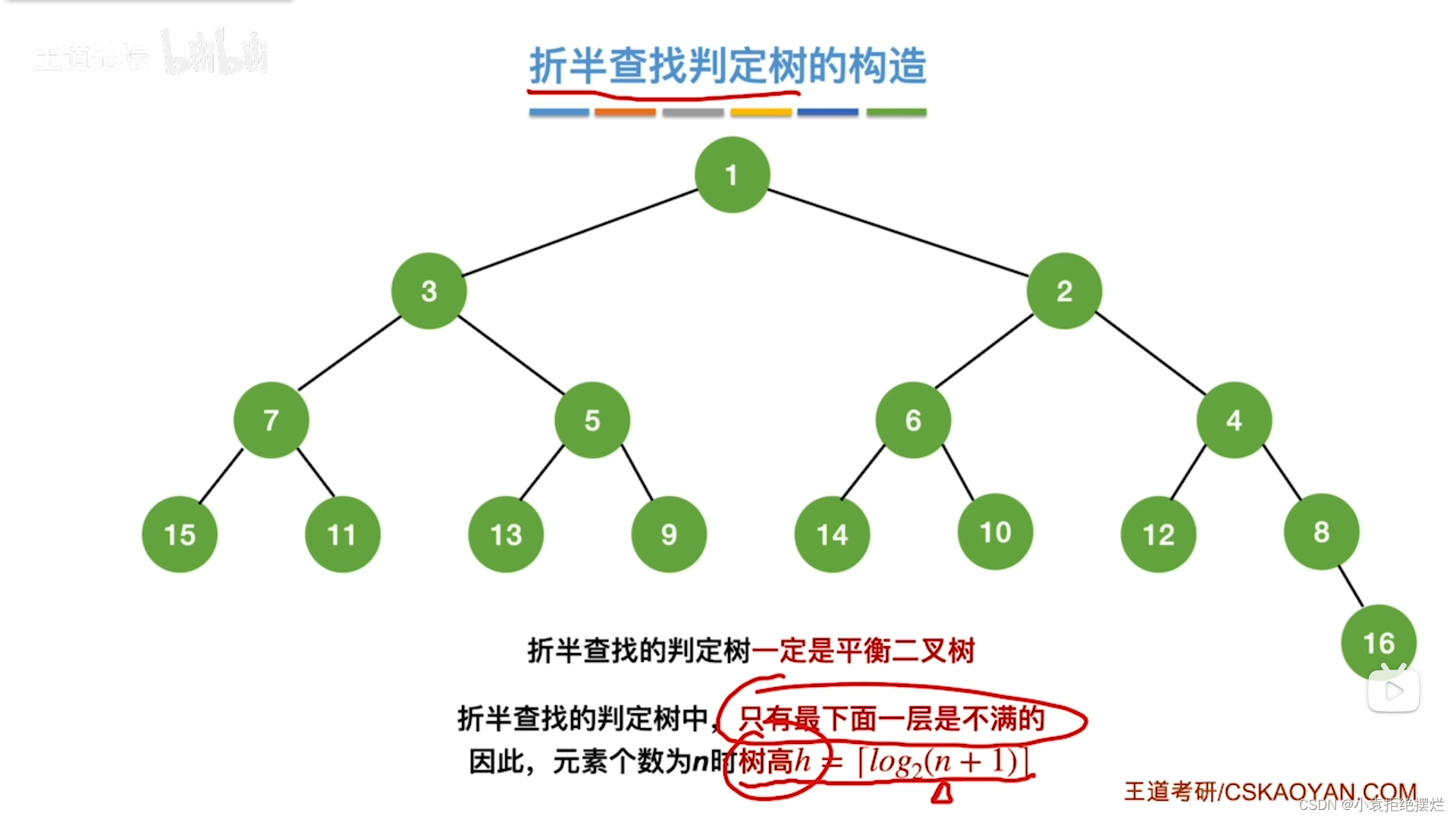

用折半查找判定树分析查找效率
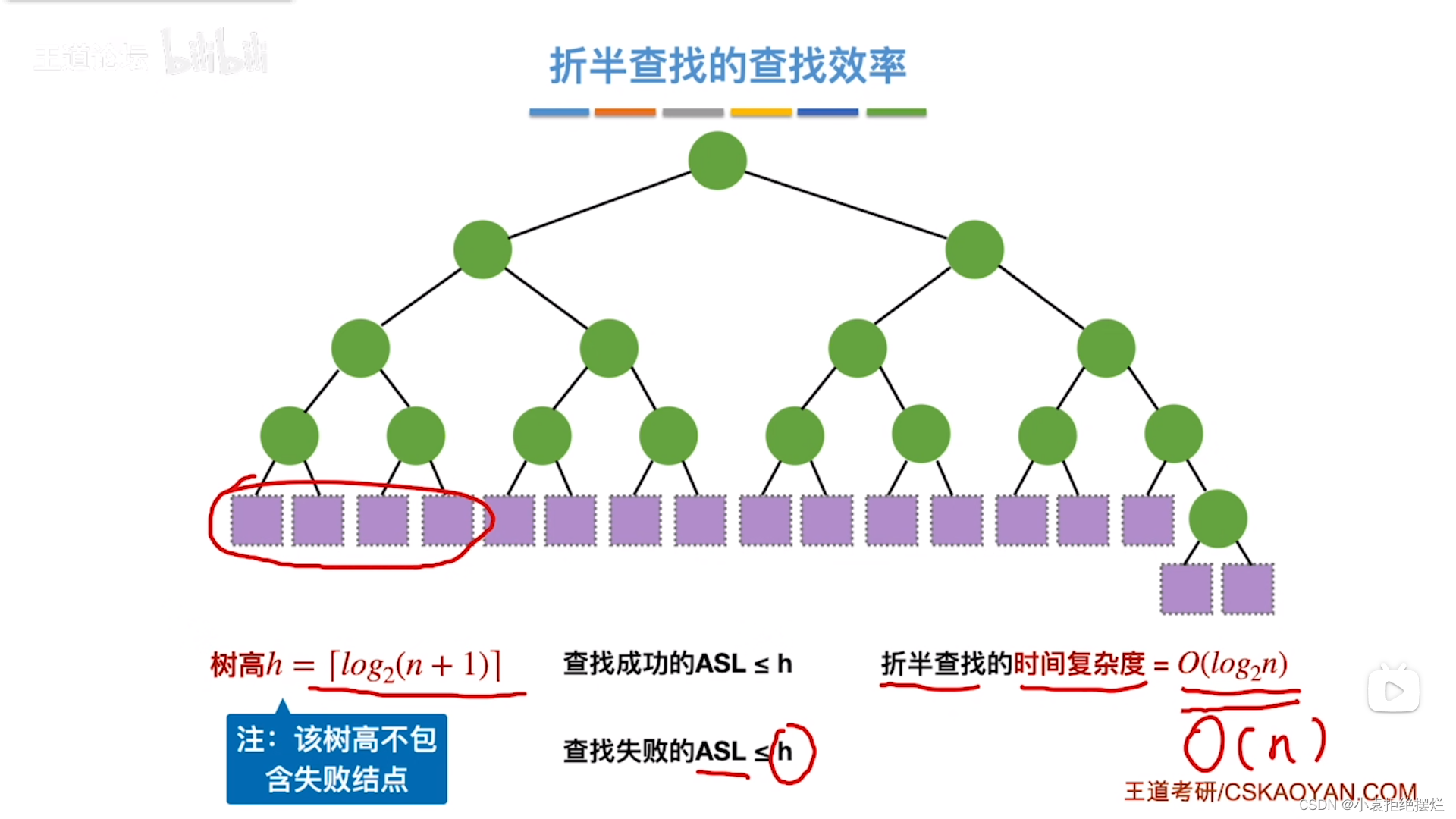
总结
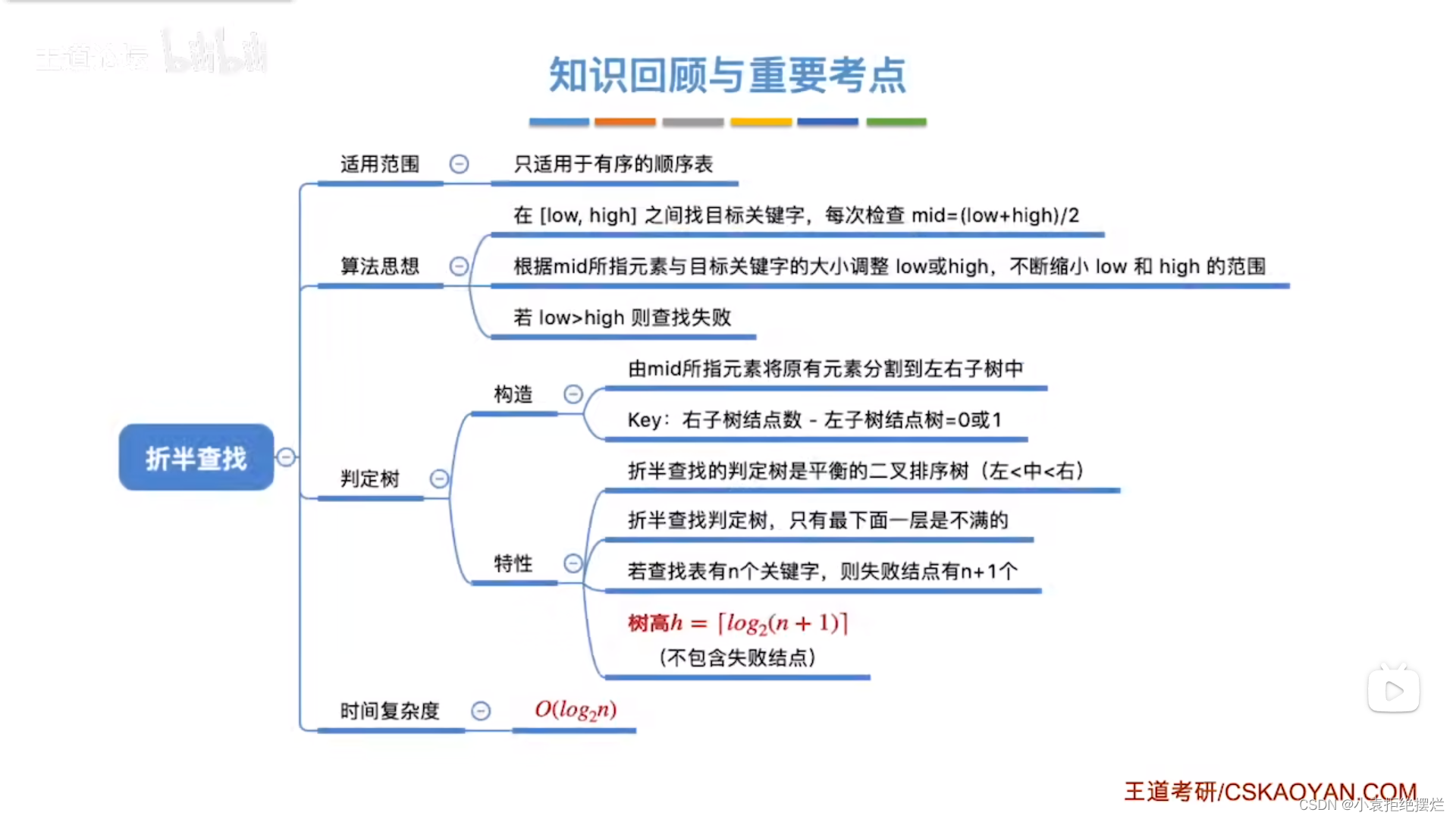





 本文详细介绍了折半查找(二分查找)算法的工作原理,特别强调了其适用于有序顺序表的特点。通过实例展示了查找过程,包括如何确定中间值、调整查找范围,并分析了在不同元素数量下的查找效率。此外,还探讨了折半查找与平衡二叉树的关系,以及如何通过折半查找判定树来评估查找效率。
本文详细介绍了折半查找(二分查找)算法的工作原理,特别强调了其适用于有序顺序表的特点。通过实例展示了查找过程,包括如何确定中间值、调整查找范围,并分析了在不同元素数量下的查找效率。此外,还探讨了折半查找与平衡二叉树的关系,以及如何通过折半查找判定树来评估查找效率。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










