Q:12 个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
分析:
- 方便起见设定 2n2n 个人排队, 这样的话每排 nn 个人,第一排的第一个人一定是最低的哪一个,同样最后一排一定是最高的哪一个。
- 假设人的身高为 , f(2n)f(2n) 表示 2n2n 个人排队方式的数量。
下面来看看 f(2n)f(2n) 和 f(2n−2)f(2n−2) 间的关系:
选择从第一列分析(也可以从最后一列分析),选择这里分析,是因为第一排第一个数已确定,只用分析第二排第一个数即可。这个数最小可以取2,最大可以取 2n−n+12n−n+1 (第二排 n 个数,最后一个为 2n), 因此 这个数有 (2n−n+1)−2+1=n(2n−n+1)−2+1=n 中可能。在这 n 个数中随便选取一个后,拿掉第一列,剩下的就是 2n−22n−2 个人的排队问题了, 并且f(2n)=n∗f(2n−2)f(2n)=n∗f(2n−2)
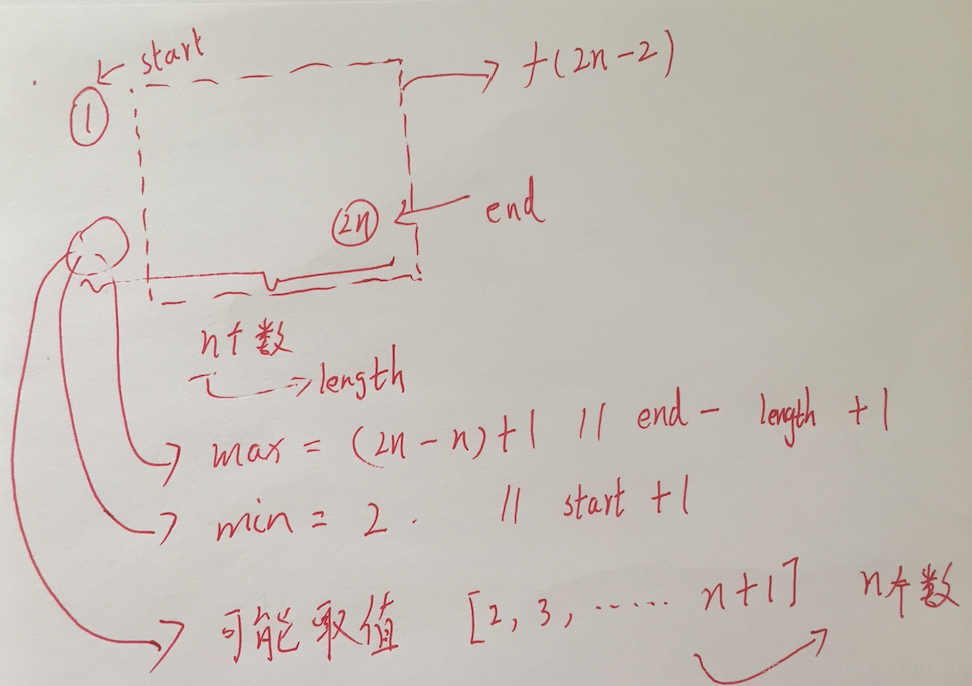
依次类推下去,得到 f(2n)=n!f(2n)=n!
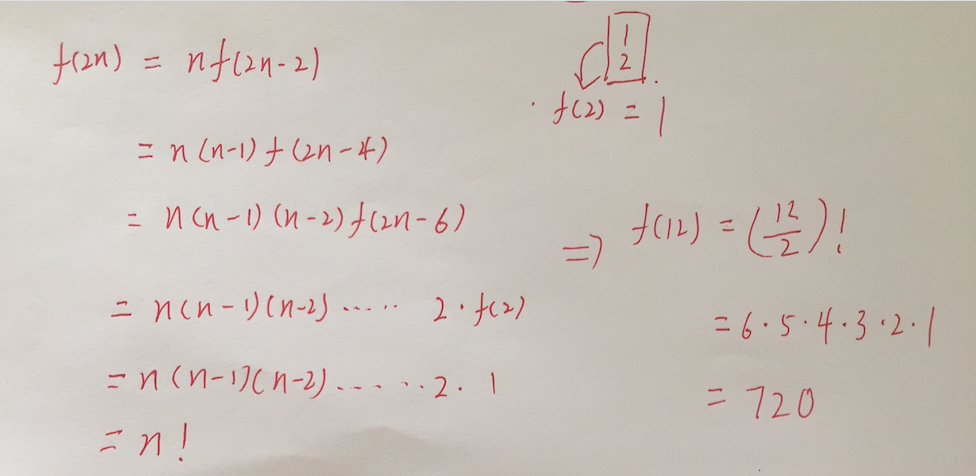
因此f(12)=6!=720f(12)=6!=720
代码就省略了,求一个数的阶乘代码不会写的话,赶快再去找本书看看吧。
 12人特殊排列计数
12人特殊排列计数





 探讨12个高矮不同的人排成两排,每排从矮到高排列,且第二排对应的人更高,计算所有可能的排列数量。通过递归分析得出,12人的排列方式共有720种。
探讨12个高矮不同的人排成两排,每排从矮到高排列,且第二排对应的人更高,计算所有可能的排列数量。通过递归分析得出,12人的排列方式共有720种。
















 5613
5613

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








