[LeetCode 6.14] Cheapest Flights Within K Stops-优快云博客

本文介绍了一个算法问题，即在给定的城市和航班价格网络中，从源城市到目标城市的最便宜路径，同时考虑不超过k次转机的约束条件。文章探讨了两种解决方案，包括回溯算法（超时）和使用堆优化的更高效方法。

Cheapest Flights Within K Stops

There are n cities connected by m flights. Each flight starts from city u and arrives at v with a price w.

Now given all the cities and flights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.

example 1:

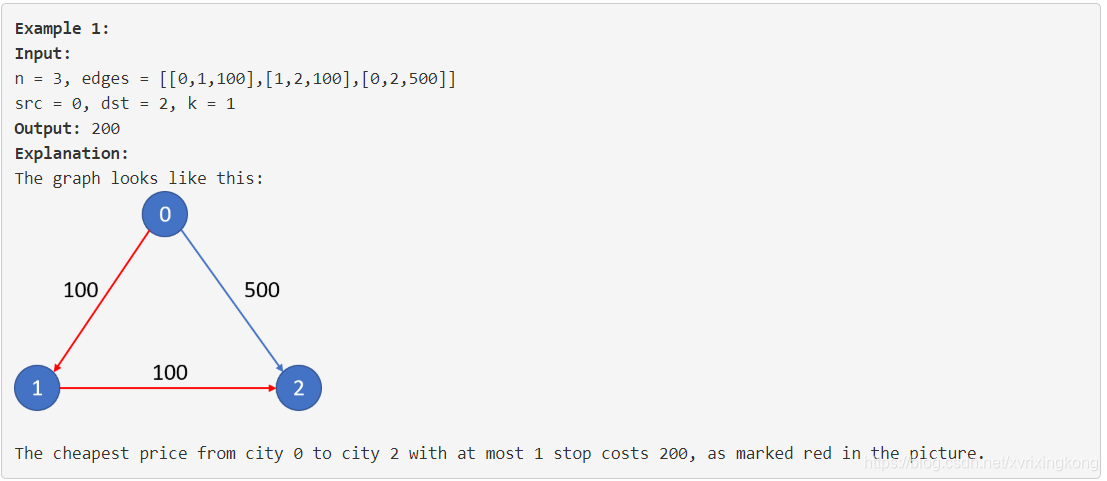
在这里插入图片描述

example 2:

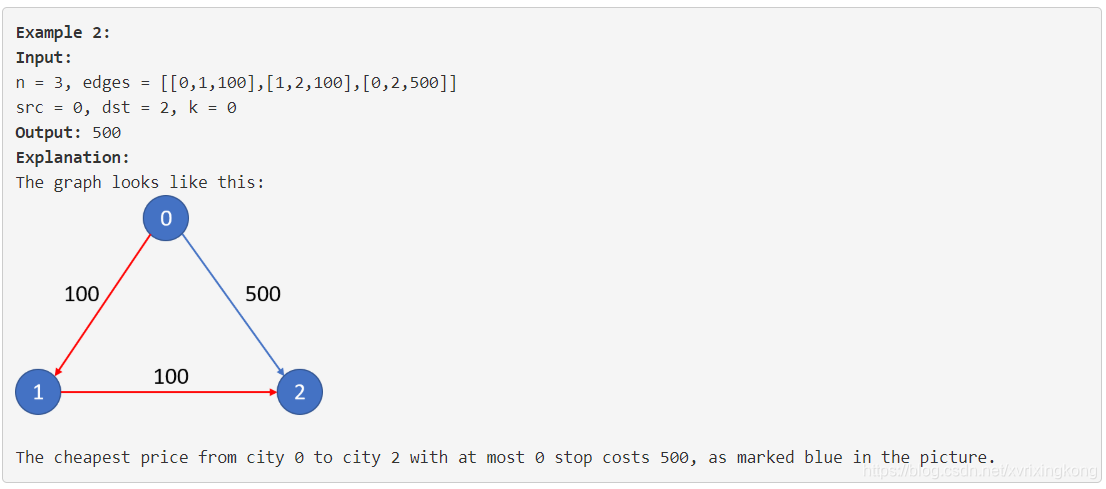
在这里插入图片描述

Constraints:

The number of nodes n will be in range [1, 100], with nodes labeled from 0 to n - 1.
The size of flights will be in range [0, n * (n - 1) / 2].
The format of each flight will be (src, dst, price).
The price of each flight will be in the range [1, 10000].
k is in the range of [0, n - 1].
There will not be any duplicated flights or self cycles.

Python3 Solution:

版本1，回溯-Time Limit Exceeded

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:
        edge = [ [[0, 0] for _ in range(n)] for _ in range(n) ]
        for a, b, price in flights: # 构建有向图
            edge[a][b] = [1, price]
        visited = [0]*n
        self.res = float('inf')

        def backtrack(node, cost, count):
            if count > K:
                return 
            if node == dst:
                self.res = min(self.res, cost)
                return 
            for i in range(n):
                if edge[node][i][0] == 1 and visited[i] == 0:
                    visited[i] = 1
                    backtrack(i, cost+edge[node][i][1], count+1)
                    visited[i] = 0

        visited[src] = 1
        backtrack(src, 0, -1)
        return -1 if self.res == float('inf') else self.res

版本二利用数据结构堆，来优化版本一

每一层都对cost最小的优先操作，找到目标解之后立即返回。

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:
        f = collections.defaultdict(dict)
        for a, b, p in flights:
            f[a][b] = p
        heap = [(0, src, K + 1)]
        while heap:
            cost, i, K = heapq.heappop(heap)
            if i == dst:
                return cost
            if K > 0:
                for j in f[i]:
                    heapq.heappush(heap, (cost + f[i][j], j, K - 1))
        return -1