一、题目描述
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:
如果有大量输入的 S,称作 S1, S2, … , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
致谢:
特别感谢 @pbrother 添加此问题并且创建所有测试用例。
示例 1:
输入:s = “abc”, t = “ahbgdc”
输出:true
示例 2:
输入:s = “axc”, t = “ahbgdc”
输出:false
提示:
0 <= s.length <= 100
0 <= t.length <= 10^4
两个字符串都只由小写字符组成。
二、题目解析
1、双指针,枚举t的全部可能的开始位置
外层for循环以t为基准,针对每个可能的起始位置,逐个匹配s的全部元素(在枚举的过程中可能包含无用操作))
如abcdh dh 其实起始位置a、b、c都是无效的,却还要遍历完dh才可以拿到结果。
class Solution {
public boolean isSubsequence(String s, String t) {
if(s == null || t == null || s.length() > t.length()){
return false;
}
//特例:空字符串
if(s.length() == 0 && t.length() == 0){
return true;
}
for(int i = 0;i <= t.length() - s.length();i++){
//每一轮开始寻找的时候都重置两个指针和计数器
int pointer1 = i,pointer2 = 0,count = 0;
while(pointer1 < t.length() && pointer2 < s.length()){
if(s.charAt(pointer2) == t.charAt(pointer1)){
count++;
pointer1++;
pointer2++;
}else{
pointer1++;//因为是序列,s的下一个位置可能符合
}
}
//这轮寻找匹配到了s的全部长度元素
if(count == s.length()){
return true;
}
}
return false;
}
}
时间复杂度O((n-m)*m),空间复杂度O(1)
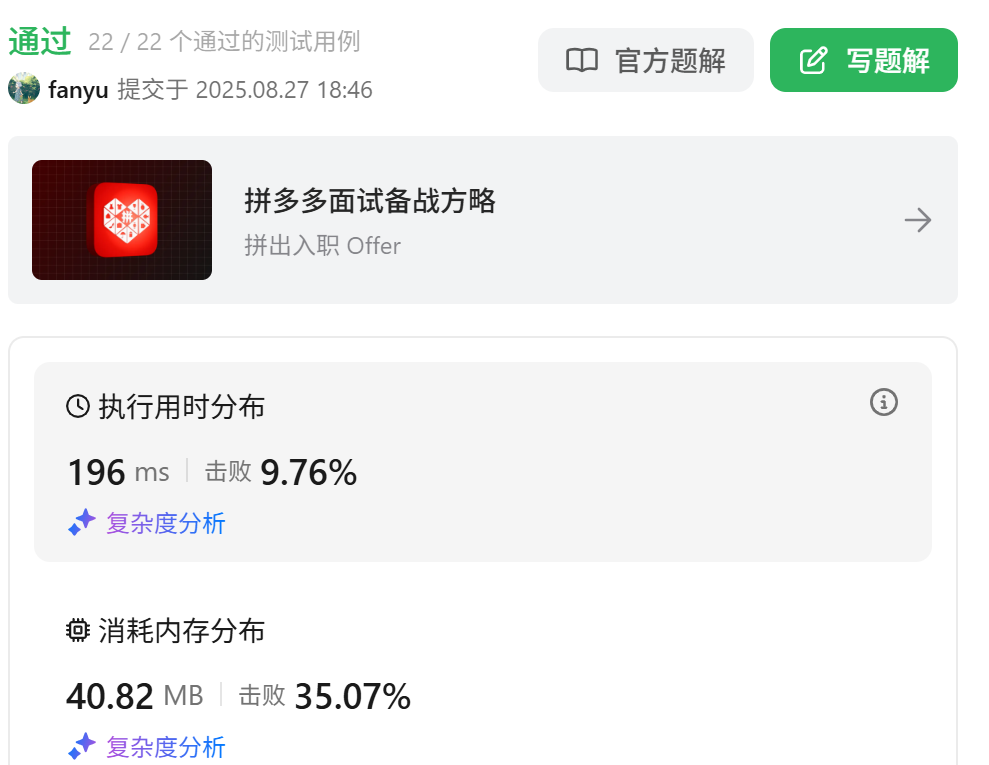
2、在1的基础上代码优化
外层for循环以s为基准,可以只遍历一遍t。
备注:和寻找子串的区别是, 一轮下来如果找不到就证明没了(因为字符串t遍历完了); 但是子串由于要求连续,如果一轮没找到,需要枚举下一个位置重新开始找。
for循环的判断处理逻辑如下:
当 s[i] == t[j] 时,代表匹配成功,此时同时 i++ , j++ ;
进而,若 i 已走过 s 尾部,代表 s 是 t
的子序列,此时应提前返回 true ;
当 s[i] != t[j] 时,代表匹配失败,此时仅 j++ ;
class Solution {
public boolean isSubsequence(String s, String t) {
if (s.length() == 0) return true;
for (int i = 0, j = 0; j < t.length(); j++) {
if (s.charAt(i) == t.charAt(j)) {
i++;
if (i == s.length()){
return true;
}
}
}
return false;
}
}
时间复杂度O(n)(n为字符串t长度,最差遍历完),空间复杂度O(1)
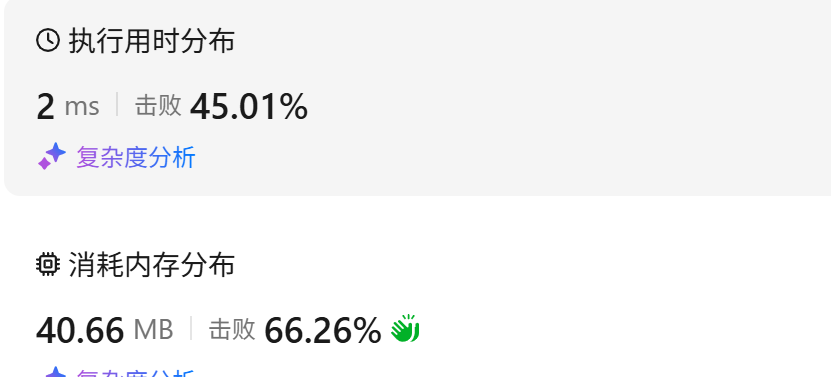





















 628
628

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








