LCR 176. 判断是否为平衡二叉树

一、题目描述

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例 1：

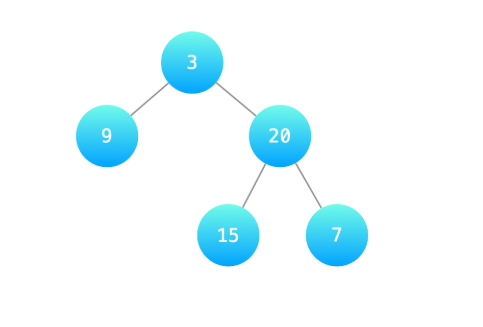
输入：root = [3,9,20,null,null,15,7]
输出：true
解释：如下图

示例 2：

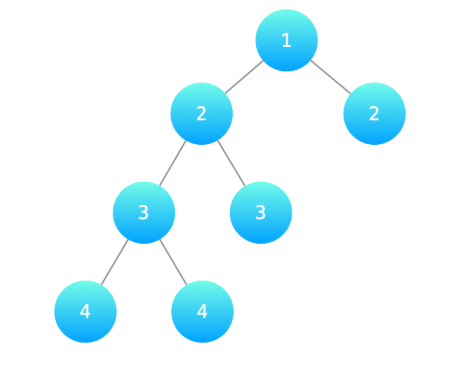
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false
解释：如下图

提示：

0 <= 树的结点个数 <= 10000

二、题目解析

1、常规思路
从顶到底判断深度，引入一个获取当前子树深度的函数，比较左右子树深度差，若满足平衡，则依次比较左子树和右子树是否为平衡。
先获取左右子树高度，再得出中间节点为根节点的树是否平衡，本质上是一种先序遍历。
缺点：产生大量重复的计算，性能比较差

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        return Math.abs(findHeight(root.left)-findHeight(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);

    }
    public int findHeight(TreeNode node){
        if(node == null){
            return 0;
        }
        // if(node.left == null && node.right == null){
        //     return 1;
        // }
        return Math.max(findHeight(node.left),findHeight(node.right)) + 1;
    }
}

2、优化版本
对二叉树做后序遍历，自底至顶返回左右子树深度，左右子树深度差都满足平衡树，则返回当前中间节点深度max（左子树深度，右子树深度）+1；若存在子树不是平衡树则进行剪枝直接返回-1，中间节点最后按照-1返回上层

class Solution {
    public boolean isBalanced(TreeNode root) {
        return recur(root) != -1;
    }

    private int recur(TreeNode root) {
        if (root == null) return 0;
        int left = recur(root.left);
        if(left == -1) return -1;
        int right = recur(root.right);
        if(right == -1) return -1;
        return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
    }
}

作者：Krahets
链接：https://leetcode.cn/problems/ping-heng-er-cha-shu-lcof/solutions/159235/mian-shi-ti-55-ii-ping-heng-er-cha-shu-cong-di-zhi/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。