隐私保护通配符模式匹配增强

隐私保护通配符模式匹配的一种增强方法

塔沙尔·坎蒂·萨哈(B)和小柴健史
日本埼玉大学科学与工程研究生院数学、电子与信息学系，樱花区埼玉市下大久保255号，邮编338‐8570{s15dm054,koshiba}@mail.saitama‐u.ac.jp

1 引言

模式匹配计算（PMC）在生物特征识别认证、语音和图像识别、生物信息学、搜索引擎、法医学等领域有广泛应用。现在，计算机专业人员和科学家正在思考如何在不向公众泄露任何信息的情况下安全地进行这些计算。因此，加密是保护数据安全的技术之一。但为了安全性，我们需要对加密数据进行计算。因此，里维斯特等人提出的同态计算是一种解决方案。[1]。此外，数据正日益增长。因此，用户不仅希望将其在线存储不仅为了节省本地计算机的空间，还可随时随地从全球访问数据。亚马逊、谷歌、微软等云服务提供商提供了大规模的存储服务以及计算能力。但与此同时，保护数据安全以及在加密数据上进行搜索也变得至关重要。同态加密（HE）使得服务提供商能够为用户提供此类服务。然而在早期阶段，戈德瓦塞尔和米卡利[20],、埃尔·加马尔[21],、科恩和费舍尔[22],、帕耶[23]的密码系统仅支持单一的同态运算，即加法或乘法，无法同时支持两者。2005年，博内等人实现了同时执行两种操作的可能性[3]，但其局限性在于只能进行多次加法和一次乘法。随后，盖内特[4]在同态计算领域实现了革命性突破，其方法可对加密数据执行多种操作，被称为全同态加密（FHE），支持多次加法和乘法运算。

然而，FHE的问题在于生成的密文ct体积庞大，导致处理速度缓慢[5]。此项突破之后，布拉克斯基等人提出了另一种部分同态加密（SwHE），支持多次加法和较少的乘法运算[6]，从而减小了密文ct大小，并提升了计算性能。2011年，劳特等人[2]展示了SwHE在医疗、金融、广告及定价领域的若干实际应用。随后，安田等人[8]提出了基于[2]的SwHE用于分析个人DNA序列的安全模式匹配应用。但他们未在其研究中解决包含通配符（*）的模式（如 ‘AT*G’、‘AT*’、‘*AT’等）的匹配问题。为弥补这一不足，他们提出了一种基于SwHE的通配符模式匹配技术，用于搜索真实世界中的基因组数据[7]。他们采用了[8]的打包方法，以匹配包含单个通配符的模式，该通配符可替换实际基因组数据文本中的一个字母。例如，在DNA字母集 Σ={A,C,T,G}中，模式‘AT*’可匹配‘ATC’、‘ATG’、‘ATA’等任意文本。

在此研究中，安田等人[7]仅考虑了模式中出现的通配符字符替换文本中一个字母的情况。但在实际中，可能需要将文本中的多个字母替换为模式中出现的同一个通配符字符，我们称这种情况为重复通配符模式匹配。本文旨在加密域中解决这一重复通配符模式匹配问题。因此，本研究关注的是在云数据库文本中安全地搜索类似‘AT*CG*AAG*TT*AGG’的模式，其中‘*’可替换文本中的一个或多个字母。实际上，我们的研究动机来源于mtDB中使用的DNA搜索方法（参见 http://www.mtdb.igp.uu.se/ 获取在线DNA搜索版本），其中通配符‘*’被表示为一个间隔。本研究仅处理一种通配符符号‘*’。若需支持其他符号，将增加该方法的时间复杂度。

1.1 最近的安全模式匹配技术

模式匹配计算可以通过两种方式实现安全保护，即特定应用协议和通用协议。我们重点讨论特定应用协议。2008年，贾等人实现了姚氏协议以用于安全基因组计算[9]。在此，他们展示了在划分后对姚氏协议进行修改的协议将问题实例分解为更小的子电路，并在参与者之间共享每个子电路的评估结果。2010年，布拉顿等人展示了使用有限自动机进行DNA搜索的安全模式匹配技术[10]。同年，卡茨等人通过修改姚氏混淆电路方法，提出了一种用于私有DNA模式匹配的新关键词搜索协议[11]。对于上述情况，它们并未处理包含通配符字符（*）的任何模式，而该通配符需要与实际文本相匹配。到目前为止，我们观察到，包含单字符通配符的安全模式匹配计算（SPMC）最早由巴伦等人在 2012[12]中提出。他们提出了一种新协议，支持更具表达性的搜索查询，包括单字符通配符以及任意字母表的子串模式匹配。此后，德夫拉维等人对一些安全模式匹配（SPM）协议进行了比较研究，并测量了它们在通配符模式匹配中的性能[15]。但迄今为止讨论的所有方法均未解决模式中出现的重复通配符问题。为了解决此类模式匹配，哈扎伊等人首次提出了针对SPM问题若干重要变体的多个协议，这些协议比之前的协议效率显著提高[16]。然而，这些协议不适用于云计算环境，因为它们未展示在云环境中的任何实现过程。因此，迫切需要一种新的方法来解决这一问题。

1.2 我们的贡献

在我们的研究中，我们重点探讨使用安田等人提出的对称部分同态加密方案在云端实现SPMC[7]。此外，通配符模式匹配在搜索真实世界基因组数据方面具有重要意义[7]。但上述少数方案仅在模式中使用了一个通配符字符，用于替换文本中的多个字母以搜索基因组数据。在此情况下，用户可能还希望在模式中使用重复通配符来搜索其基因组数据。因此，我们需要一种方法，能够有效支持此类通配符出现情况下的SPM。进一步地，我们希望使用的模式如“ AC*CTA*T”，可匹配诸如“AACGGCTATTACAACTGGT”之类的任意序列。若采用[7]的方法，则此处需要九次同态乘法运算，但我们希望找到一种仅需少量同态乘法即可完成该操作的方法。为实现这一新目标，我们提出了一种协议和一种新的打包方法，使我们能够基于对称部分同态加密方案实现隐私保护通配符模式匹配。我们的打包方法是对安田等人[14]方法的改进版本，旨在防止当数据规模超出其限制时计算过程中发生的溢出问题。

1.3 结构概述

本文的组织结构如下。第2节描述了云环境下的安全模式匹配及其协议和一些典型应用。此外，在第3节中描述了用于我们模式匹配协议的同态加密方案及其安全性与正确性。另外，我们在第4节讨论了所提出的打包方法。我们的模式匹配计算是在第5节中讨论。我们还在第6节中从理论和实践两方面叙述了我们的协议的性能。最后，我们在第7节中总结了本文。

2 云中安全模式匹配

在早期的安全模式匹配研究工作中，大多数研究既不适用于重复通配符模式匹配，也不适用于云计算。一些研究人员[7,8,14]提出了可应用于云环境的贡献，但他们未处理包含此类通配符的模式。因此，我们将在接下来的小节中讨论使用对称SwHE的SPM协议及其应用。

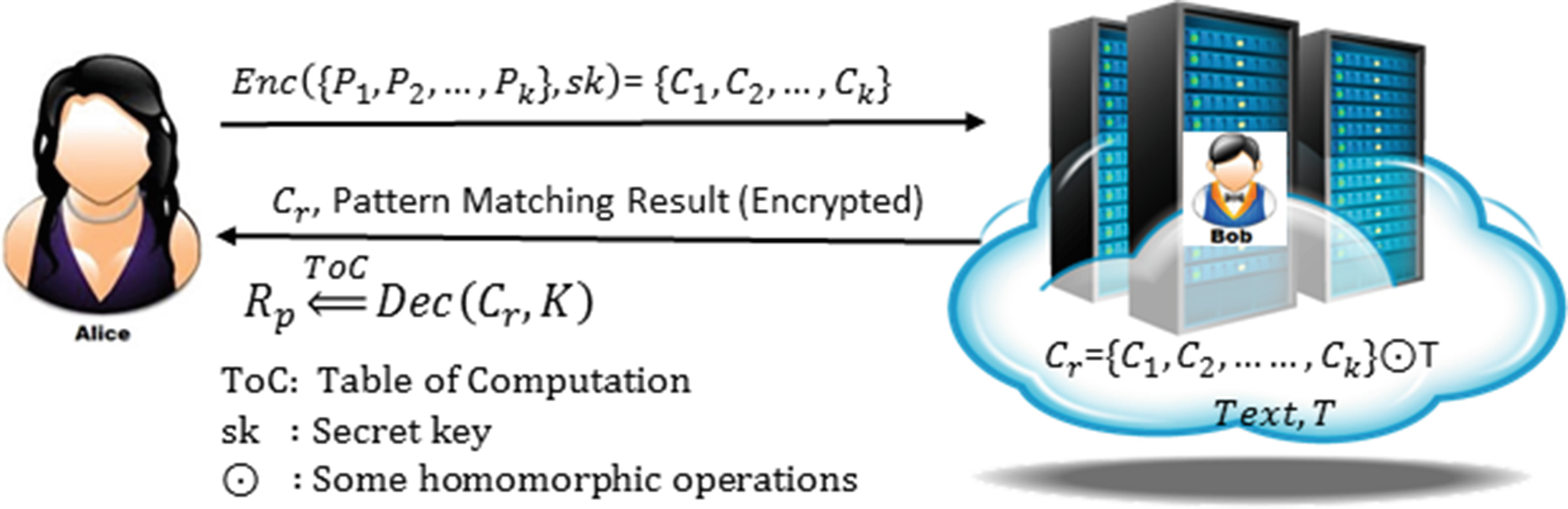
2.1 我们的协议使用对称SwHE

为了描述该协议，我们考虑爱丽丝与鲍勃之间进行安全模式匹配的一个场景。例如——鲍勃在他的安全服务器上存储了长度为 l的明文 T=(a0, . . . , al−1)，该服务器具有强大的计算能力。此外，爱丽丝有一个包含一些通配符的模式 P=(b1,0b1,1 ··· b1,p1−1 ∗b2,0b2,1 ··· b2,p2−1 ∗ ··· ∗ bk,0bk,1 ··· bk,pk −1)，该模式可在明文 T中找到。这里爱丽丝将该模式划分为不含通配符字符的子模式{P1, P2,…, Pk}，其子模式的长度向量为(p1,p2, . . . ,pk)，其中 pk ≤ l。但爱丽丝不希望向鲍勃泄露她的模式。相反，鲍勃也不能将其服务器内的信息泄露出去。因此，同态加密属性[1]可以处理这种情况。全同态加密能够执行任意操作，但具有较大的时间复杂度。在本例中，部分同态加密[7]更为适用。此外，鲍勃可以通过测量 T的子文本与P的每个子模式之间的平方欧几里得距离来进行模式匹配计算。对于 0 ≤ d ≤(ly − py) 和 1 ≤ y ≤ k，子文本 T d与每个子模式 P y 之间的平方欧几里得距离 Edis通过以下公式计算。

$$
Edis= \sum_{h=0}^{p_y-1} (a_{d+h} - b_{y,h})^2 \quad (1)
$$

此外，如图1所示，我们的协议可以通过以下几点简洁地描述。

1. 爱丽丝有一个包含多个通配符的模式 P，她将该模式 P分解为不包含通配符字符的子模式{P1, P2,…, Pk}，并使用自己生成的同态密钥对这些子模式进行加密。
2. 然后，她将加密后的模式发送给鲍勃，以执行安全搜索。
3. 鲍勃通过公式(1)在文本 T与子模式{C1, C2,…, Ck}之间执行所需的模式匹配计算，并将包含加密位置的结果返回给爱丽丝。
4. 爱丽丝使用她的密钥解密结果，并利用我们的‘计算表’来考虑通配符，从而获得她期望的结果。

备注1。 在此，我们的协议在鲍勃为半诚实（也称为诚实但好奇）的假设下是安全的，即他始终遵循协议但试图从协议中获取信息。

2.2 典型应用

SPMC在应用场景方面具有广泛的应用领域。此外，数据规模正在迅速增长。在安全性是主要考虑因素的安全计算需求中，例如患者的电子健康记录、人类基因组数据库、数字取证、生物信息学、网络入侵检测等场景均需要安全计算。医疗中心可以将其患者的数据上传到云服务器，从而患者可允许医生查阅存储在数据库中的医疗报告或DNA记录。由于Genbank数据库[17]公开可用，其中包含带注释的DNA序列集合，模式匹配技术目前被广泛使用。Genbank实际上 是国际核苷酸序列数据库协作的一部分，该协作包括日本DNA数据库(DDBJ)、欧洲分子生物学实验室(EMBL)以及国家生物技术信息中心(NCBI)的 Genbank数据库。模式匹配还可用于法医应用，从大量数字内容中搜索特定的数字内容以保护版权。我们希望我们的打包方法和协议能够对云计算平台上的多种模式匹配应用有所帮助。

使用的符号。 符号 Z表示整数环。对于一个素数 p，整数环用 Z p表示。对于向量 A=（a0, a1,…, an−1），其最大范数为 ‖a‖∞= max |ai|。令 〈T, P〉表示两个向量 T和 P之间的内积。密文ct ctadd和ct ctmul分别表示文本 m′与加密文本 ct= Enc（m, sk）的同态加法和乘法。此外，b y ,i y 表示第 y个子模式的第i y 个字符。分布 D Z n表示 n维离散高斯分布。

3 使用同态加密的安全性

在本节中，我们回顾了[7]的对称SwHE方案及其正确性。2011年，布拉克尔斯基和瓦伊昆塔纳坦[6]提出了该方案的正确性。

3.1 对称SwHE方案

安田等人[7]提出了一种基于[2]的公钥SwHE方案的对称SwHE。对于该方案，我们需要考虑以下一些参数：
– q：模数 q是一个奇素数，满足 q ≡ 1(mod 2n)，用于定义密文空间的环 Rq= R/qR= Zq[x]/f(x)。
– f(x)：一个分圆多项式，其中 f(x) = xn+ 1。
– n：一个整数，表示环 Rq=Zq[x]/f(x)的格维度，同时也表示多项式的次数，该次数为2的幂，例如1024或2048。
– σ：一个参数，用于定义离散高斯误差分布χ= DZn,σ，实际中以标准差 σ= 4 ∼ 8表示。
– t：一个素数 t< q，用于定义该方案的消息空间为 Rt= Zt[x]/f(x)，即模 f(x)和 t的整数多项式环。

现在我们可以讨论该方案的密钥生成、加密、同态性和解密特性，如下所示：

密钥生成。 为我们的密钥 sk= s 生成一个环元素 R s ← χ；
加密。 对于给定的明文 m ∈ Rt，加密算法首先采样a ← Rq和 e ← χ，然后加密可由密文对(c0, c1) =ct定义如下：
$$
Enc(m, sk)=(c0, c1)=(as+ te+ m,−a)
$$

同态操作。 通常，同态操作如加法（）和乘法（）是在两个密文之间进行的。但在我们的情况下，其中一个是明文 m′，另一个是密文 ct= Enc（m, sk）。因此，我们的密文 ct=（c0, c1）与明文 m′之间的同态操作可以定义为
$$
\begin{cases}
ct_{add}= ct m′=(c0 m ′, c1) \
ct_{mul}= ct m′=(c0 m ′, c1 m ′)
\end{cases} \quad (2)
$$
其中明文 m′在上述计算中被视为 R q 中的一个元素。我们也可以类似加法一样定义减法，即 ct (−m)′=(c0 (−m)′, c1)。

解密。 对于密文 ct ∈(Rq) 2 和 t ∈ Rt，使用私钥 sk= s 可定义一般解密为
$$
Dec(ct, sk)=[m ˜] q \mod t \quad \text{where} \quad m˜= c0+ c1s.
$$
在以同样的方式，同态解密可以通过以下方式定义 :
$$
\begin{cases}
Dec(ct {add}, sk)=[m ˜ {add}]_q \mod t \
Dec(ct {mul}, sk)=[m ˜_{mul}]_q \mod t
\end{cases}
$$
其中 m˜add= c0+ m′+ c1s 和 m˜mul= c0m′+ c1m′s。

3.2 该方案的安全性

我们可以基于带误差多项式环学习（ring‐LWE）假设来证明该方案的安全性，正如劳特等人所做的那样。[2]。设环 Rq= Zq/f(x)，其中 f(x)=(xn+ 1) 是关于次数为 n的分圆多项式。令 s ← Rq为一个均匀随机的环元素。该假设由任意多项式数量的如下形式的样本给出
$$
(ai, bi= ai · s+ ei) ∈(Rq)^2
$$
其中 ai在 Rq中均匀随机，而 ei从误差分布 χ中抽取。这里的 bi在计算上与在Rq中的均匀分布不可区分。因此，很难将(ai, bi)与一个均匀随机的数对(ai, bi)区分开来。此外，Lyubashevsky等人[18]指出，环LWE假设可归约到理想格上问题的最坏情况困难性，而该困难性被认为可抵御量子计算机的攻击。

备注2。 最近，Castryck等人[25]提出了环上LWE的可证明弱实例。但这类弱实例不会影响我们的方案。

3.3 该方案的正确性

该方案的正确性取决于解密过程如何在执行某些同态操作后从密文ct中恢复原始结果。我们可以将解密过程写为
$$
\begin{cases}
Dec(ct_{add}, sk)= Dec((ct m′), sk)= m+ m′ \
Dec(ct_{mul}, sk)= Dec((ct m′), sk)= m· m′
\end{cases} \quad (3)
$$
实际上，上述过程已在[6]的第1.1节中进行了描述。此处，密文ct ct来自 m ∈ Rq加密后的结果以及另一段明文 m′ ∈ Rq。第3.1节中的加密方案是 SwHE的体现，若以下引理成立，则该方案成立，如[7]所示。

引理1（成功解密的条件）。 对于密文 ct，当解密 Dec(ct, sk)满足 〈ct, s〉 ∈ R q 在模 q下不发生环绕时，即条件 ‖〈ct, s〉‖∞ < q / 2 成立时，能够恢复正确结果。其中令‖a‖∞= max |ai| 表示元素 a= ∑ n−1 i=0 aix i ∈ R q 。具体而言，对于新鲜密文ct，其 ∞-范数 ‖〈ct, s〉‖∞由 ‖m+ te‖∞给出。此外，对于同态运算后的密文，其 ∞-范数可通过公式(2)计算。

4 安全模式匹配的打包方法

由于篇幅限制，此处我们跳过对[2,13]的一些早期打包方法的回顾。然而，安田等人[7]实现了[13]的打包方法，用于基于对称SwHE的隐私保护通配符模式匹配。对于类似“AT*”的模式，在DNA字母表上匹配某些DNA序列“ATA”、“ATT”、“ATG”和“ATC”时，他们需要进行三次同态乘法。在他们的研究中，使用模式中的通配符字符来替换文本中的单个字母。但我们希望考虑如图 2(a)所示的DNA序列和模式。此处模式中存在一些间隙，可用通配符字符表示。如果我们将该模式拆分为子模式，则会得到4个不同的子模式。为了将这些子模式与给定的DNA序列进行匹配，我们需要4次查询，即采用[7]的方法需要12次乘法运算，如图2(b)所示。但如果希望如图2(c)所示，通过一次查询并使用较少的乘法运算完成匹配，则需要一种不同于[13]的打包方法。

设 T为文本向量， P为可表示为T=（a0， a1， a2，…， a(l−1)） ∈ Z l 和 P=（b1,0b1,1 ··· b1,p1 −1 ∗ b2,0b2,1 ··· b2,p2 −1 ∗ ··· ∗bk,0bk,1 ··· bk,pk −1) ∈ Z |P|分别对应。此处， T的长度为 l，其中 l ≤ n.¯此外，模式 P可被划分为 k个子模式，表示为 P={P1, P2,…, Pk}，忽略通配符，这些子模式的长度可表示为{p1,p2,…, pk}。我们知道，模式匹配通常通过测量相同长度的文本与模式之间的距离来实现。因此，我们需要测量每个子模式与文本中相同长度的每个子串之间的距离。这里，我们可以通过将这些距离作为 {x的次数} x的不同次数的系数，构造一个 n次多项式，从而得到文本与各个子模式之间的距离。因此，如果我们采用[13]的打包方法，将所有子模式打包成一个模式，大多数子模式的模式匹配结果将会以x的某些次数的系数形式发生环绕。这样一来，就很难从结果多项式中提取每个子模式匹配结果。因此，有必要将每个子模式匹配结果作为¯不同x的次数 x的系数获取。现在我们需要以不同于[13]的打包方式对模式 P进行打包。为了解决上述问题，即避免任何x的次数下系数的环绕，我们为 Py