Motion in an Externally Generated Velocity Field（外生速度场中的运动）

1 Convection（对流）

假设，对于模糊表面上的每个点，我们都有一个速度，当每一个点上的度量函数成立，那么对我们来说，就是可知的。

为了讲模糊表面上的所有点都有一个速度，于是有了速度场的概念：

于是我们给出了一个常微分方程：

 

因为对边界的离散化过程，会使得边界不在平滑、规律。为了规避这些问题，我们让模糊函数即表示边界，又进化边界。

模糊函数的进化过程定义如下：

其中，下标t表示对时间变量t的偏导数。是梯度符号，有如下公式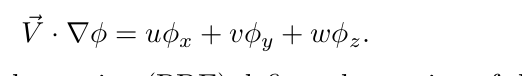：该方程就是水平设置函数（level set method）

这个方程还有另外一个比较受欢迎的形式：

在笛卡尔网格中，要求速度场不仅在的边界上，在边界外也要有定义，此时等式32才会成立。

所以对于边界之上增加band的概念，来对应上面说的边界外。我们让作为函数零水平集合。

 

举个例子：

在这个区域内，除了在边界上，其他地方的速度场都为0.，边界上为：

从而，然后确切的解决方案是以速度1向右移动的边界。但是因为在笛卡尔网格中，点并不是都在边界上的，因此这些不在边界上的就等于0 ，从而会使得等式3.2中的这一项消失。从而意味着，在每个地方成立，，

所以边界大多不正确。

这时候，该怎么办？这个困难的问题可以部分地通过对速度场上的一些条件设置一些条件来纠正.

1. 要足够平滑， 通过引入边界的带宽厚度，其中要求足够小从而来最小化变量

2.要连续

取样问题=+最小化

  Step1: 由于边界上给出的值决定了边界的运动，因此无论怎么样变化，这些运动时不变的

  Step2: 离开边界的速度与正确的边界运动无关。通过将边界速度限制垂直边界方向上恒定，可以获得速度场的最小变化。

==

3.2 逆差分

一旦我们在笛卡尔网格的每个点上定义了和，我们可以应用数值方法来演化在时间上向前移动跨越网格的边界。

在某个时间点用表示，函数的当前时间内的值用。当时间发生变化，即产生了时间增量，则此时函数变为：其中

forward Euler 方法即对等式3.2的时间离散化之后的一阶精确方法，其公式如下：

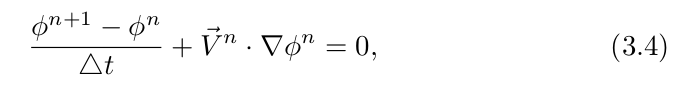
其中，在时间内，给出的外部速度场，，是在时间内，使用函数的值来评估梯度操作符。

的偏导数用常shishishishifoweorweorEFQAEFQEADF规的方法是不行的，在数值离散化偏微分方程时，通常需要非常小心。

1. 我们先对3.4进行改写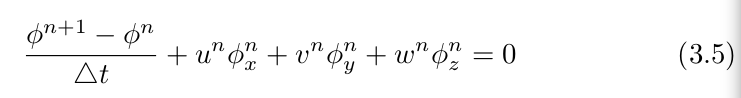，然后我们先来解决对项进行评估。为了简化计算，我们在一维空间内考虑等式3.5，有如下公式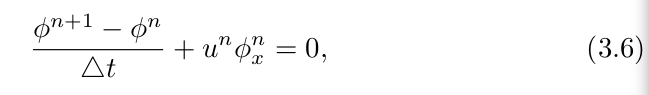：，其中符号指明了是往左移动还是往右移动。因为可以在空间上进行变化，我们则关注一个特定的网格点有如下公式：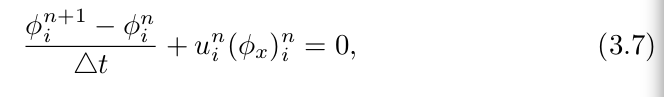

其中，表示在点处的导数。如果，则表示从左--->右，告诉我们在的左边看一下，确定在时间步长结束时落在点上的值。如果，则表示从右--->左，这种情况我们应该关注

的右边，在时间确定的适当值。
 

​，被用于接近​当​。

​，被用于接近当。

通过的符号，来选择导数的接近，这种方法被称为upwinding .

upwinding的具体分解流程如下：

1. 对与每一个网格点，用来代替，用来代替。当，用来接近，当，用来接近。当会消失。

用upwind difference与forwar Euler time 的结合来离散的方法，就是对偏微分等式3.2的一个一致的有限差分近似。根据Lax-Richtmyer等价定理，线性偏微分方程的有限差分近似是收敛的，即，当且仅当它是一致且稳定时，获得正确解为。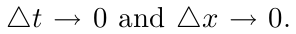

Courant-Friedreichs-Lewy condition可以加强稳定性，这个条件要求数据波的传播速度要和物理传播速度一样快甚至更快。因此有CFL时间约束如下：。其中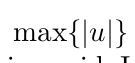要求时整个网格中最大的值。但实际当中我们只需要选边界上最大的就可以。

添加的选择，公式３．８变为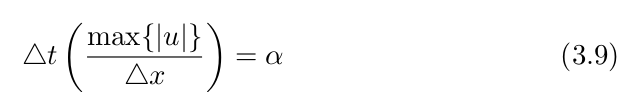，其中

多维的ＣＦＬ表达式为：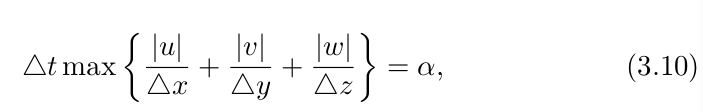

 

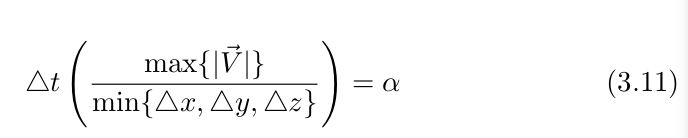
增加稳定性的另一种方法：

在方程（3.2）的右边添加一些人工耗散来获得，

其中粘度系数选择与成比例，这样人工粘度随着的消失而消失，使这种方法具有一致性。