1. 树
参考链接:
1.1 基本概念
在计算机科学中,树(Tree)作为一种抽象的数据结构,用来模拟具有树状结构性质的数据集合,表示一对多的对应关系,考虑它的各种特性,来解决我们在编程中碰到的相关问题。它是由n(n≥0)个结点组成的一个具有层次关系的有限集合,之所以把它叫做”树”,是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。树的定义就是在讲解栈时提到的递归的方法,即在树的定义之中还会用到树的概念。

与栈、队列、链表不同,树是一种非线性的数据结构。一棵树只能有一个根结点,拥有多个根结点的数据结构是树的集合,即森林。
实际在现实生活中,树状结构是十分普遍的。例如在我们的计算机磁盘上存储的文件夹和文件,就能够构成一个文件树结构。其中,盘符下存储有文件和文件夹,文件夹下又有子文件和子文件夹,但是文件之下一定不会有其他子文件和子文件夹。如果将这些层次关系表示成一棵树,其结构如下:

通过上面这张图我们可以看出:
-
通过盘符或者文件夹,我们只能向下访问其中的子文件和子文件夹,但是我们不能够从文件夹1直接跳转到文件夹2中去,正如我们不会在D盘中直接访问到C盘是一样的道理;
-
只有盘符或者文件夹下面才能够下挂子文件和子文件夹,但是文件之下是不能够下挂其他任何结构的;
-
每一个盘符和文件夹之下都有多个分支,这些分支“开枝散叶”,形成了复杂的分支结构,而这种分支结构在向上看的时候,最终都会回归到盘符这个层面,所以上面这张图正如同一棵倒置的大树,其树根在上。我们将这种由结点和分支构成,并且结点之间只能够上线联系,不能够左右沟通的结构,称之为树结构。
在上图中 ,我们称所有的盘符、文件夹和文件为树结构的结点;而连接结点与结点之间的通路,称之为路径。如果一个结点指向另一个结点(例如文件夹1和文件2的关系),那么我们称上面指出的结点为父结点或者双亲结点(文件夹1);下面被指向的结点称为父结点的孩子结点(文件2),孩子结点简称子结点。
综上,引出数的基本定义如下:
-
当n=0时,称作空树;
-
当n>0时,称作非空树;
-
在任意一棵非空树中,每一个圆圈称作一个结点(结点中包含一个数据元素及若干个指向其子树的分支),每个结点有0个或者多个子结点,但有且仅有一个特定的结点称作根结点(Root),位于树的最上方,根结点没有父结点,其余的结点称作非根结点,每一个非根结点有且只有一个父结点。
-
当n>1时,除根结点外的其余结点可分为m(m>0)个互不相交的有限集T1、T2、...、Tm,其中,每一个集合本身又是一棵树,称其为根的子树(SubTree)。
-
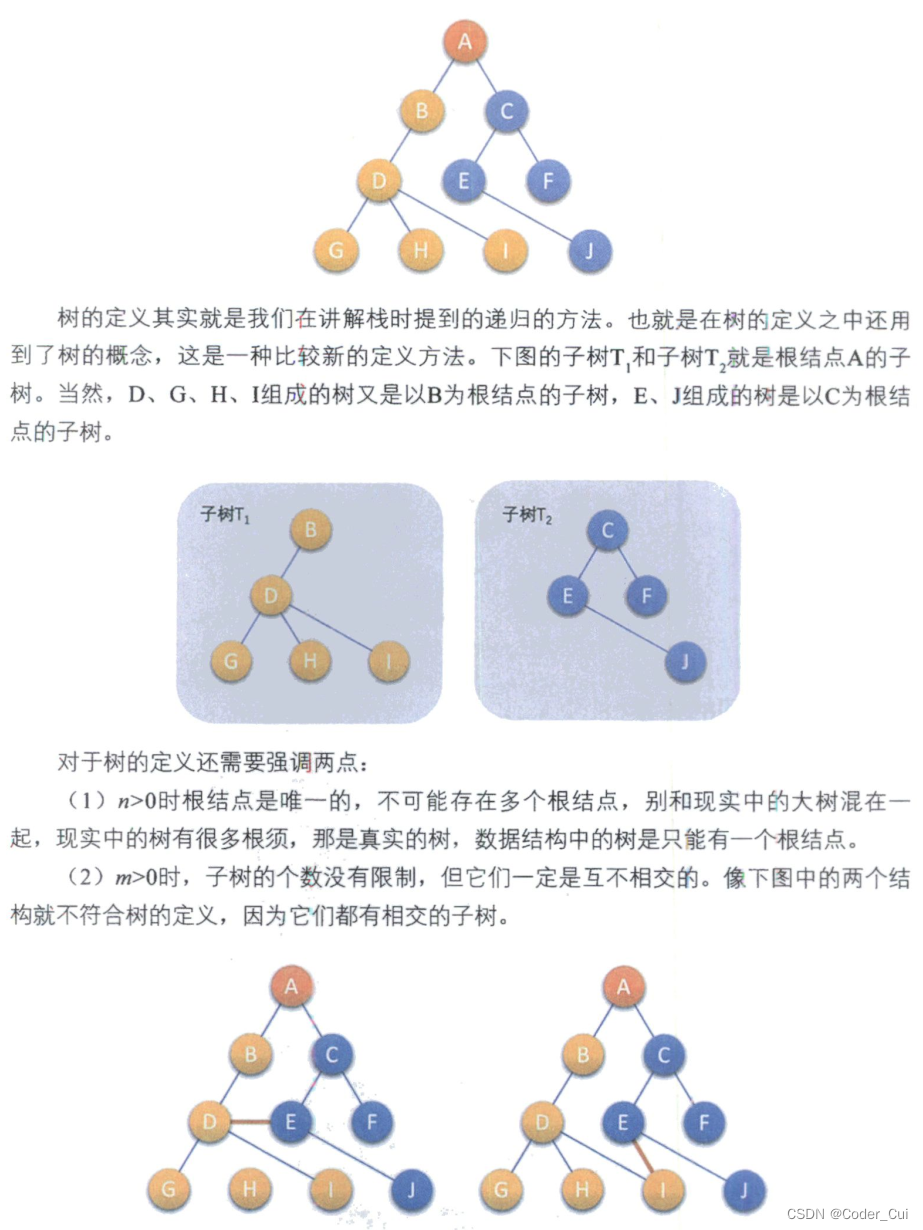
-
-
树中不存在环;
-
一个结点的直接后继结点称为该结点的孩子结点(Child)或子结点(或每一棵子树的根),习惯性的,我们将一个父结点左边的子结点称为左孩子结点,右边的子结点称之为右孩子结点;
-
一个结点的直接前驱结点称为该结点的双亲结点(Parent,雌雄同体)或父结点(或每一棵子树的根的父亲);
-
同一双亲结点的孩子结点之间互称为兄弟结点(Siblings);
-
其双亲在同一层的结点互称为堂兄弟结点。
-
结点的祖先是从根到该结点所经分支上的所有结点。
-
一个结点含有子结点个数称为结点的度(Degree),树中所有结点度的最大值称作树的度。

-
度为0(即没有子结点)的结点称为叶结点(Leaf) 或 终端结点 或 叶子结点;
-
度不为0的结点称作分支结点或非终端结点,除根结点外,分支结点也称为内部结点或中间结点;
-
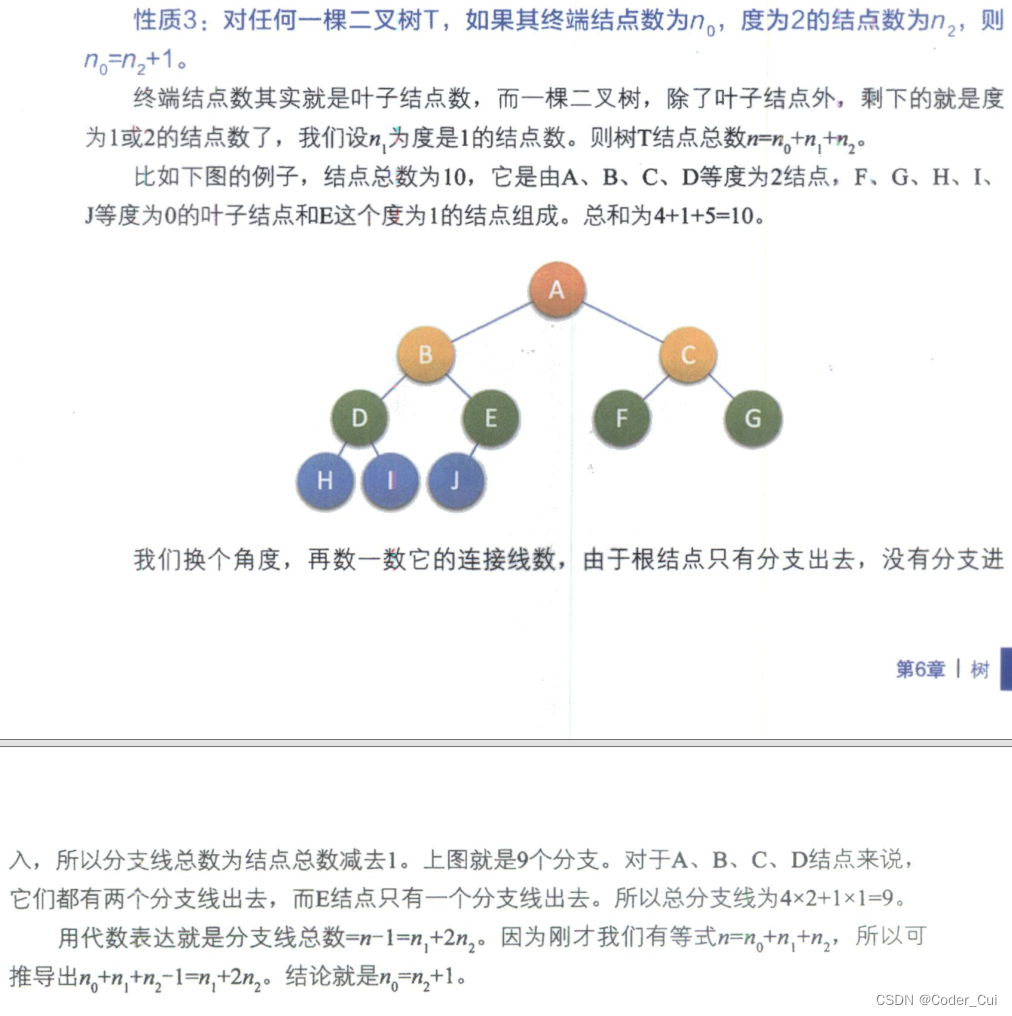
在许多面试题中,都使用n0、n1、n2分别表示度为0、度为1、度为2的结点的数量,即有0个孩子结点、1个孩子结点、2个孩子结点的结点数量。
-
在任意一棵二叉树中,这些结点的数量之间存在着如下关系:
-
n2 = n0 - 1:即度为2的结点个数总比度为0的结点个数少1,也就是说,在任意二叉树中,同时具有左右孩子的结点,总比叶子结点的数量少1个;
-
根据上式可推导出如下关系:n = n0 + n1 + n2 = 2 * n0 + n1 - 1 = n1 + 2 * n2 + 1,且n1 = n - n0 - n2 = n - 2n0 + 1 = n - 2n2 - 1,其中,n表示结点总数。
-
因此只要我们知道一个二叉树中总的结点个数以及度为0或者度为2的结点数量,就能够推导出其他度的结点数量。
-
-
-
-
结点的层次(Level):从根结点开始算起,根结点的层次为第一层,根的直接后继(孩子)层次为第二层,以此类推,即:若某结点在第n层,则其子树就在第n+1层。将树中的结点按照从上层到下层、同层从左到右的次序进行展开,可以得到一个线性序列(此处与下面的结论存在问题:树中结点的最大层次称为树的深度(Depth)或高度(Height))。

上图中,D、E、F是堂兄弟,G、H、I、J也是堂兄弟。树的深度为4。
-
对于任意结点Ni,Ni的深度(Depth)为从根结点到Ni的唯一的路径的长,因此,,根结点的深度为0。Ni的高度(Height)是从Ni到一片树叶的最长路径的长,因此,所有叶子结点的高都是0。一棵树的高等于它的根的高,一棵树的深度等于它的最深的树叶的深度,该深度总是等于这棵树的高。
-
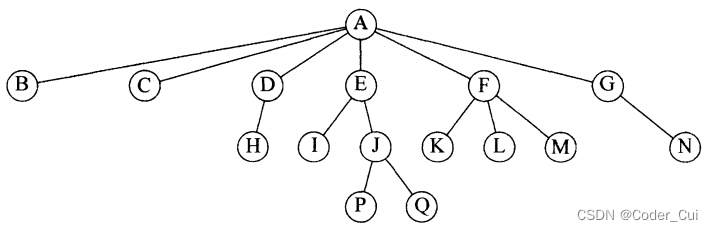
结点E的深度为1,高度为2;结点F的深度为1,高度为1;树高=树深=3
-
从递归的定义中可以发现,一棵树是由N个结点和N-1条边的集合,其中的一个结点叫做根。得出存在N-1条边的的结论依据:每条边都将某个结点连接到它的父亲,而除去根结点外每个结点都有一个父亲,即N个结点总共N-1条边。
-
从结点N1到Nk的路径(Path)定义为结点N1、N2、...、Nk的一个序列,使得对于1≤i≤k结点Ni是Ni+1的父亲,这条路径的长(Length)为该路径上边的条数,即k-1.从每一个结点到它自己有一条长为0的路径,注意,在一棵树中从根到每个结点恰好存在一条路径。
-
从根结点到目标结点所经历的所有结点称为目标结点的祖先结点,某一结点的子女以及这些子女的子女均为该结点的子孙结点。。如果存在从N1到N2的一条路径,那么称N1是N2的一位祖先(Ancestor),而N2是N1的一个后裔(Descendant)。如果N1≠N2,则称N1是N2的真祖先(Proper Ancestor),而N2是N1的真后裔(Proper Descendant)。
-
-
如果将树中结点的各子树看成是从左到右有次序的且不能互换的,则称该树为有序树,否则称为无序树。
-
森林(Forest):是m(m>=0)棵互不相交的树的集合,将一颗非空树的根结点删去,树就变成一个森林;给森林增加一个统一的根结点,森林就变成一棵树。对树中的每个结点而言,其子树的集合即为森林。

将线性表与树的结构进行对比如下:
-
线性表:
-
线性结构
-
第一个数据元素:无前驱
-
最后一个数据元素:无后继
-
中间元素:一个前驱、一个后继
-
-
树结构:
-
非线性结构
-
根结点:无双亲,唯一
-
叶结点:无孩子,可以多个
-
中间结点:一个双亲多个孩子
-
补充:利用递归计算阶乘
package tree;
/**
* @ClassName Recursion
* @Description 递归计算阶乘
* @Author Jiangnan Cui
* @Date 2022/10/16 15:48
* @Version 1.0
*/
public class Recursion {
public static void main(String[] args) {
System.out.println(factorial((4)));
System.out.println(factorial2(4));
}
// 1.利用for循环计算阶乘
public static int factorial(int n){
// 4!=4 * 3 * 2 * 1
int factorial = 1;
for (int i = n; i >= 1; i--) {
factorial *= i;
}
return factorial;
}
// 2.递归实现阶乘
public static int factorial2(int n){
if(n == 0){
return 1;
}
// 4! = 4 * 3!
// = 3 * 2!
// = 2 * 1!
// --> f(4) = 3 * f(3)
// = 3 * f(2)
// = 2 * f(1)
// = 1 * f(0)
// 令f(0)=1
return n * factorial2(n-1);
}
}
1.2 树的存储结构及Java实现
实现树的一种方法可以是在每一个结点除存储数据外还要存储一些链,使得该结点的每一个儿子都可以有一个链指向它。然而每个结点的儿子树并不确定,因此在数据结构中建立到各儿子结点的直接的链接是不可行的,因为这样会浪费太多的空间。
顺序存储和链式存储都不能很好地反映出树的逻辑关系,故需采用顺序和链式相结合的方式。树的存储方式主要有以下三种:
-
双亲表示法
-
孩子表示法
-
孩子兄弟表示法
1.2.1 双亲表示法
具体介绍详见:程杰《大话数据结构(溢彩加强版)》P130-P133
双亲表示法采用顺序表(也就是数组)存储普通树,其实现的核心思想是:顺序存储各个结点的同时,给各结点附加一个记录其父结点位置的变量。注意:根结点没有父结点,因此根结点记录父结点位置的变量通常设为 -1。其结构特点如图所示:
![]()
对于下图的树而言,存储状态如表所示:
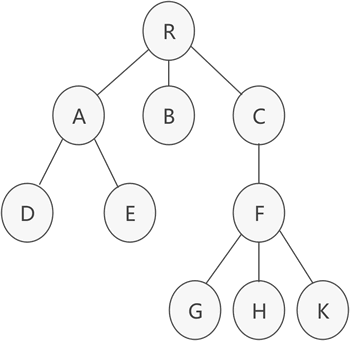
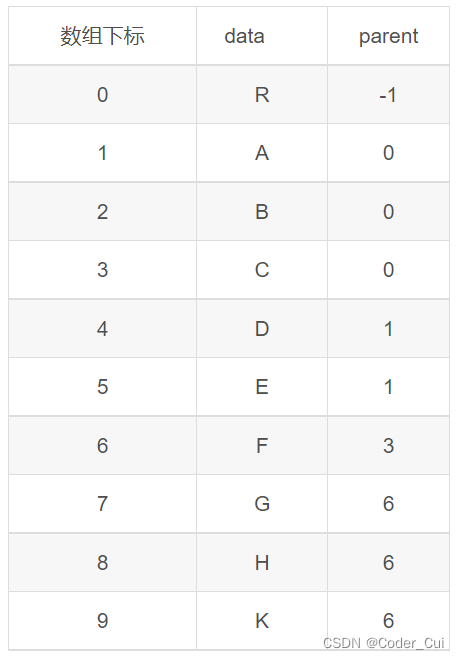
对应Java代码实现:
class TreeNode{
int data;
int parent;
TreeNode(){}
TreeNode(int val){
this.data = val;
}
}
public class Tree {
TreeNode[] treeNodes;
int n;
}
1.2.2 孩子表示法
具体介绍详见:程杰《大话数据结构(溢彩加强版)》P133-P136
孩子表示法采用顺序加链式的存储方式,首先会建立一个顺序表存储树中的各个结点,此外,孩子表示法还会在每个结点后配备一个链表,用于存储它的子女结点,无子女结点的结点对应的是空链表。存储状态示意图如下:
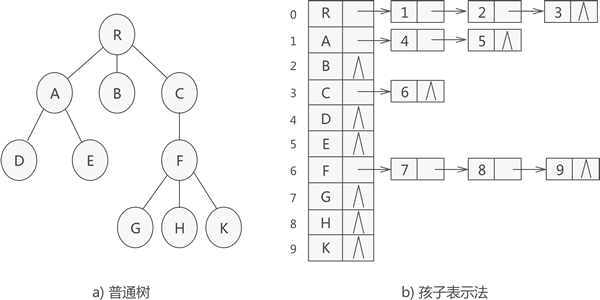
对应Java代码实现:
class TreeNode{
int val;
TreeNode next;
TreeNode(){}
TreeNode(int val){
this.val = val;
}
}
1.2.3 孩子兄弟表示法
具体介绍详见:程杰《大话数据结构(溢彩加强版)》P136-P137
孩子兄弟表示法采用的是链式存储的方式,从树的根结点开始,依次使用链表存储各个结点的孩子结点和兄弟结点,该链表中的结点分为三部分:孩子结点、数据域、兄弟结点。存储状态示意图如下:
![]()
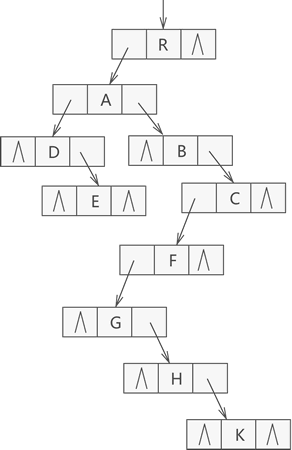
对应Java代码实现:
class TreeNode{
int val;
TreeNode child;
TreeNode brother;
TreeNode(){}
TreeNode(int val){
this.val = val;
}
}
2. 二叉树
2.1 基本概念
二叉树定义:是n(n≥0)个结点的有限结合,该集合或者为空集(称为空二叉树),或者是由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
或
如果在一棵树中,如果每个结点都最多含有2个子树(分支或子结点),即每个结点的度不超过2,那么我们称具有这种特殊的树状结构为二叉树。以此类推,树中每个结点最多具有N个分支的树状结构称之为N叉树。二叉树的结构如下所示:

即:在一棵二叉树中,一个结点要么没有子结点;如果有子结点,那么最多只有两个子节点(左孩子结点、右孩子结点)。
特点:
-
每个结点最多有两棵子树(注意此处是最多有,没有子树或者只有一棵子树也是可以的),所以二叉树中不存在度大于2的结点。
-
二叉树的左右孩子结点或左右子树均有顺序,次序不能任意颠倒。即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。
-
在二叉树的第i层上最多有 2^i-1 个节点
-
在许多面试题中,都使用n0、n1、n2分别表示度为0、度为1、度为2的结点的数量,即有0个孩子结点、1个孩子结点、2个孩子结点的结点数量:
-
在任意一棵二叉树中,这些结点的数量之间存在着如下关系:
-
n2 = n0 - 1 或 n0=n2+1:即度为2的结点个数总比度为0的结点个数少1,也就是说,在任意二叉树中,同时具有左右孩子的结点,总比叶子结点的数量少1个;
-
根据上式可推导出如下关系:n = n0 + n1 + n2 = 2 * n0 + n1 - 1 = n1 + 2 * n2 + 1,且n1 = n - n0 - n2 = n - 2n0 + 1 = n - 2n2 - 1,其中,n表示结点总数。
-
因此只要我们知道一个二叉树中总的结点个数以及度为0或者度为2的结点数量,就能够推导出其他度的结点数量。
-
-
-
-
一个具有k层的二叉树,其各层最大结点数目推导公式如下:
-
第1层:1=2^0=2^(1-1)
-
第2层:2=2^1=2^(2-1)
-
第3层:4=2^2=2^(3-1)
-
......
-
第i层:=2^(i-1)
-
......
-
第k层:=2^(k-1)
-
即:在二叉树的第k层至多有2^(k-1)个结点
-
对各层结点数目等比数列求和可知,二叉树至多有2^k-1个结点,即为满二叉树时,其叶子结点个数为2^(k-1),其各层结点实际上是一个公比为2的等比数列。
-
-
二叉树总共有以下5种形态:
-
空二叉树
-
只有一个根结点
-
根结点只有左子树(左斜树)
-
根结点只有右子树(右斜树)
-
根结点既有左子树又有右子树:满二叉树、完全二叉树
三个结点的二叉树形态如下所示:
-
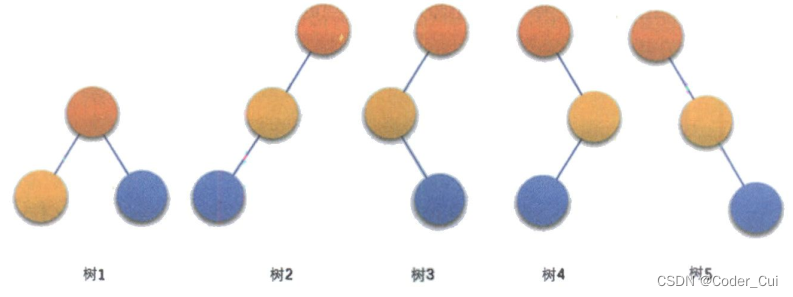
-
-
结构类比单链表:
如果我们将上述结点的结构进行调整,使每一个结点都具有两个指针域,让每一个指针都指向另一个结点,可以得到如下的数据结构:


通过上图可以看出,两种结构是等价的,因此我们只需要在单链表结点的基础上进行改动即可:
class TreeNode {
int val; // 数据域
TreeNode leftChild; // 左孩子节点
TreeNode rightChild; // 右孩子节点
TreeNode{}
TreeNode(int val){
this.val = val;
}
}
2.1.1 斜树
斜树定义:在一棵二叉树中,如果所有的结点都只有左子树的二叉树叫左斜树,所有结点都是只有右子树的二叉树叫右斜树,这两者统称为斜树,斜树最明显的特点就是每一层只有一个结点,其结点总数=二叉树的层数=二叉树的深度=二叉树的高度。线性表结构可以理解为树的一种极其特殊的表现形式。
左斜树示意图如下:

右斜树示意图如下:

2.1.2 满二叉树
满二叉树定义:在一棵二叉树中,除最后一层叶子结点无任何子结点外且均在同一层外,其余每层的父结点均含有两个子结点,即每一层的结点数均达到最大值,结点数目达到二叉树结点数目的最大值,那么就称这棵二叉树为满二叉树。满二叉树示意图如下所示:

特点:
-
叶子结点只能出现在二叉树的最下一层,出现在其它层就不可能达成平衡;
-
非叶子结点的度一定为2
-
在同样深度的二叉树中,满二叉树的总结点个数最多,叶子结点个数最多;
-
一个具有k层的满二叉树,其节点总数为2^k-1个,各层结点实际上是一个公比为2的等比数列,结点总数为2^k-1。
-
满二叉树的结点总数一定是一个奇数,因为从第2层开始,每一层的结点数量都是2的整数倍,所以最后加上根结点,那么结点总数一定是奇数,单独对上述每一层结点个数进行等比数列求和也可以证明。
-
如果按照从上到下、从左到右的方式为满二叉树的每一个结点从1开始进行编号,那么满二叉树第k层结点中的最大编号取值为2^k-1。
-
在一棵满二叉树中,编号为m的结点(父结点)和其左右孩子结点的编号关系为:
-
父结点:m
-
左子结点:2m
-
右子结点:2m+1
-
2.1.3 完全二叉树
完全二叉树定义:在一棵深度为h二叉树中,除第 h 层外,其它各层 (1~(h-1)层) 的结点数都达到最大值,且第h层所有的结点都连续集中在最左边,即如果叶子结点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树称之为完全二叉树。
或
对一棵具有n个结点的二叉树按层编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树,编号跟满二叉树编号一致。满完全二叉树结构如下所示:

特点:
-
注意:满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树,即完全二叉树不一定是满的。
-
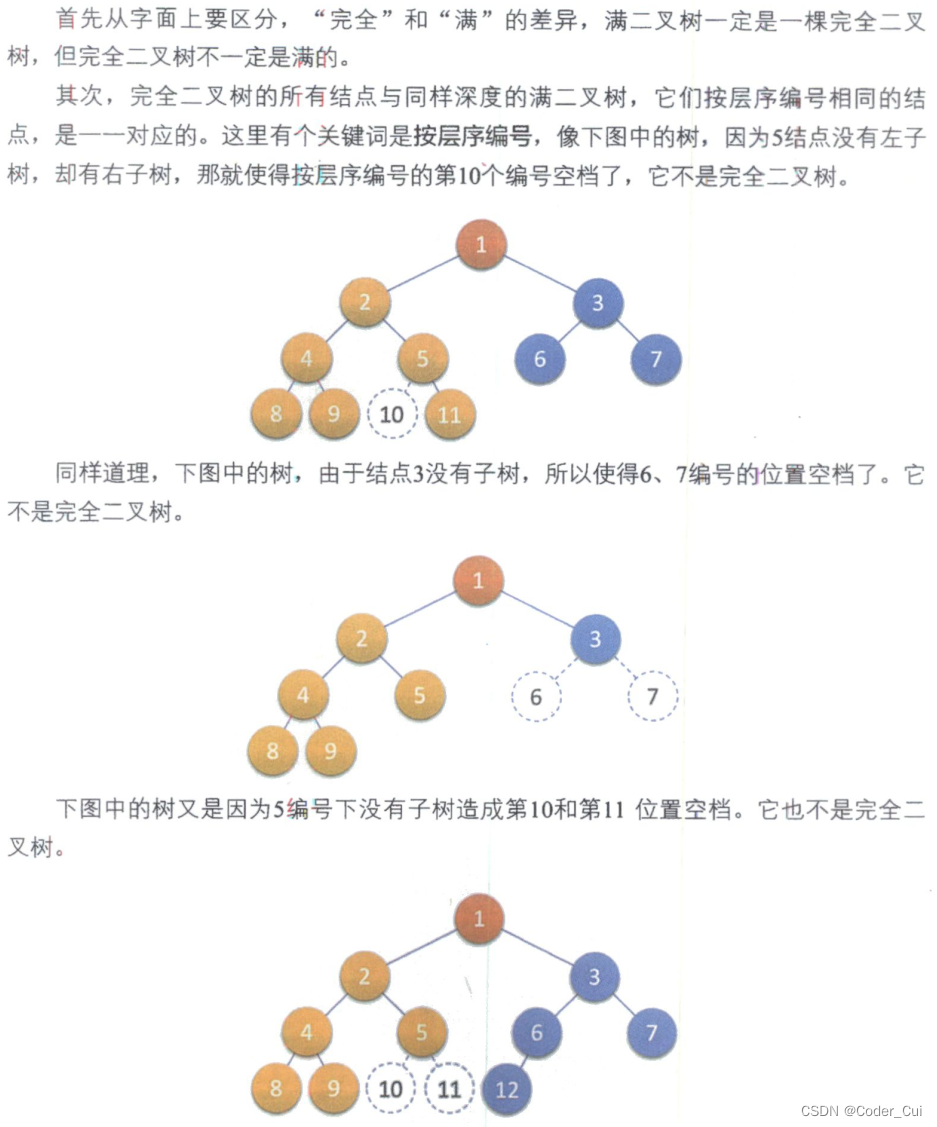
-
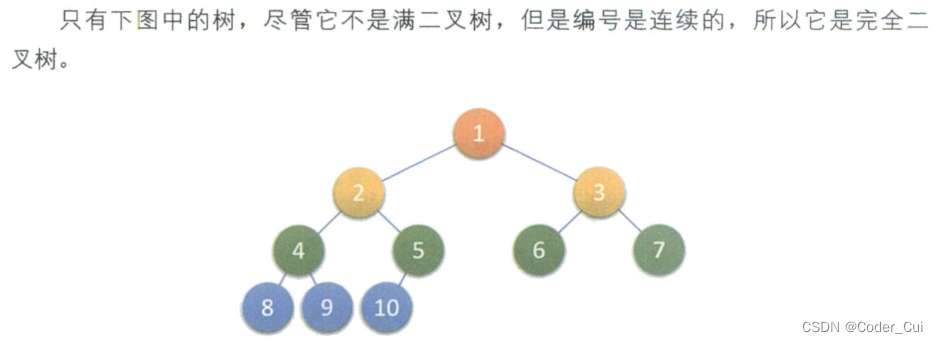
-
叶子结点只能出现在最下层和次下层
-
最下层的叶子结点集中在树的左部连续位置
-
倒数第两层,若存在叶子结点,一定在右部连续位置
-
如果结点度为1,则该结点只有左孩子,即没有右子树
-
具有n个节点的完全二叉树的深度为[log2n]+1,其中[log2n]是向下取整。同样结点数目的二叉树中,完全二叉的树深度最小。
-

-
若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 编号,则对完全二叉树中任意一个编号为 i 的结点有如下性质:
-
若 i=1,则该结点是二叉树的根,无双亲, 否则,编号为 [i/2] 的结点为其双亲结点;
-
若 2i>n,则该结点无左孩子结点, 否则,编号为 2i 的结点为其左孩子结点;
-
若 2i+1>n,则该结点无右孩子结点, 否则,编号为2i+1的结点为其右孩子结点。
-
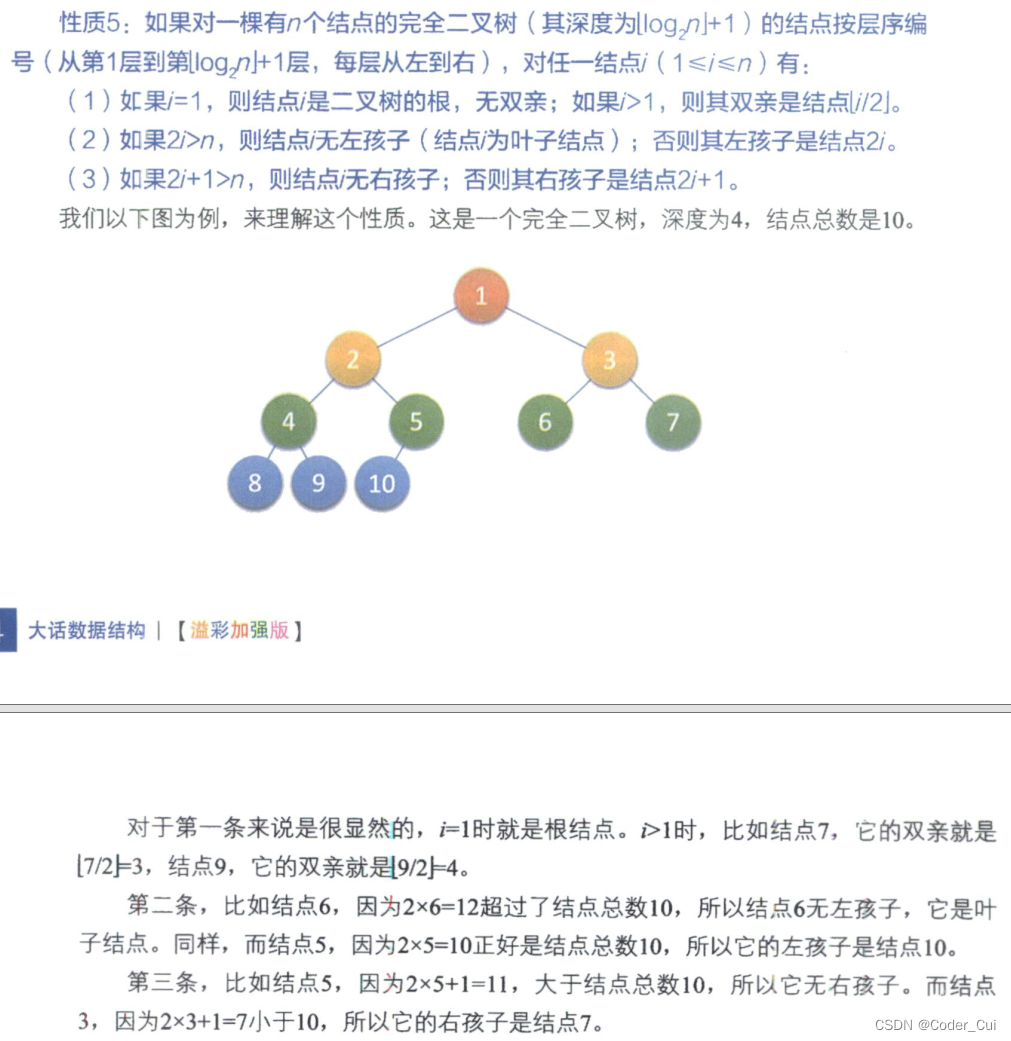
-
2.2 二叉树的存储结构
2.2.1 顺序存储结构
二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点,且结点的存储位置就是数组的下标索引。完全二叉树示例如下:

采用顺序存储方式为:

当二叉树不为完全二叉树时,该顺序存储结构又是如何?

其中浅色结点表示结点不存在,需要用^表示,那么其存储结构为:
![]()
但是在左斜树、右斜树这些极端情况下,采用顺序存储十分浪费空间。因此,顺序存储一般适用于完全二叉树。

2.2.2 链式存储结构(二叉链表)
既然顺序存储不能满足二叉树的存储需求,那么可以考虑采用链式存储。由二叉树定义可知,二叉树的每个结点最多有两个孩子。因此,可以将结点数据结构定义为一个数据域和两个指针域。结点结构图如下所示:

class Node TreeNode{
T data;// 数据
TreeNode leftChild;// 左子节点 或 左孩子指针
TreeNode rightChild;// 右子结点 或 右孩子指针
}

2.3 二叉查找树/二叉搜索树(ADT)
参考链接:
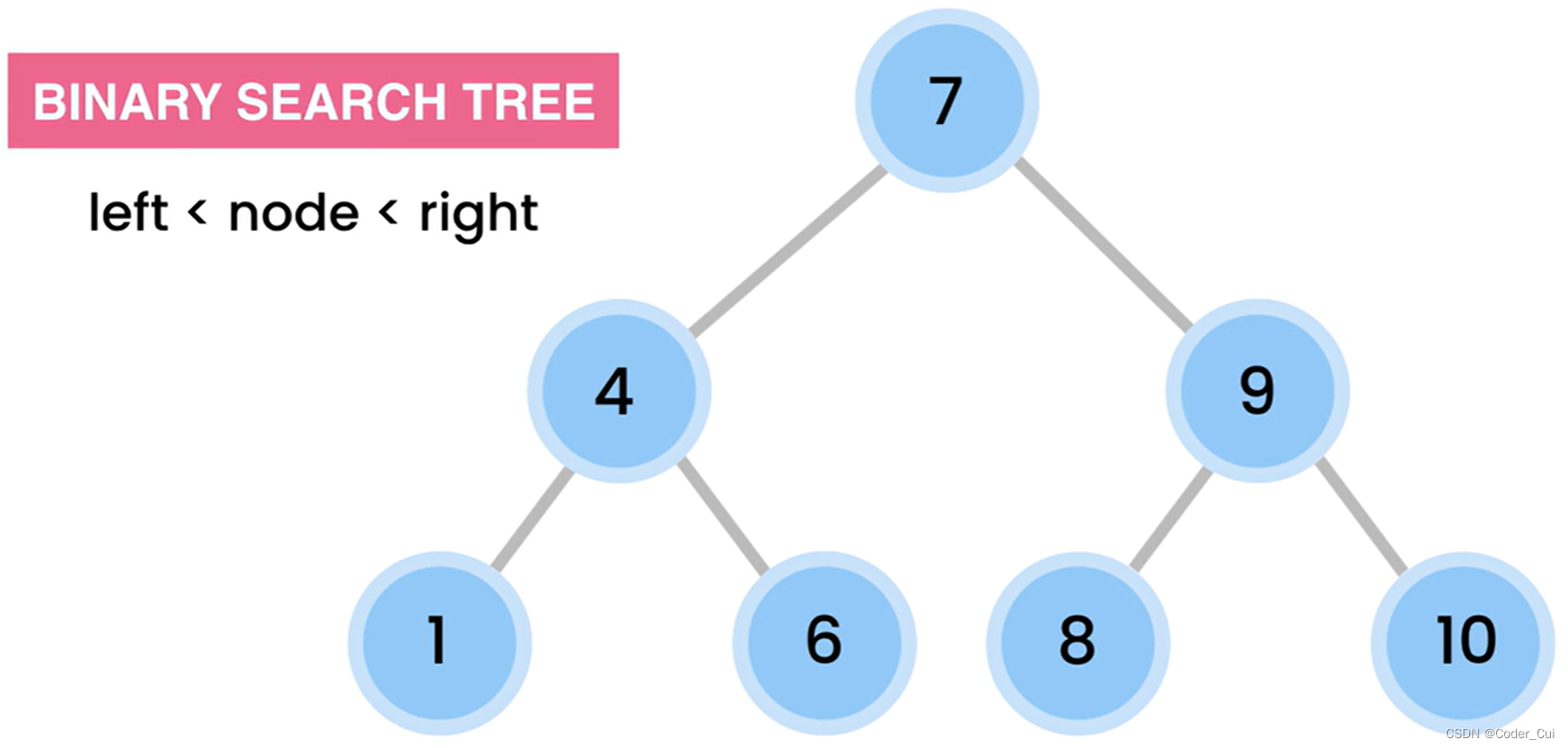
二叉查找树(ADT):对于树中的某个结点X,它的左子结点的值都比X小,它的右子结点的值都比X大,即值大小依次为:左 < 根< 右,示例如下:
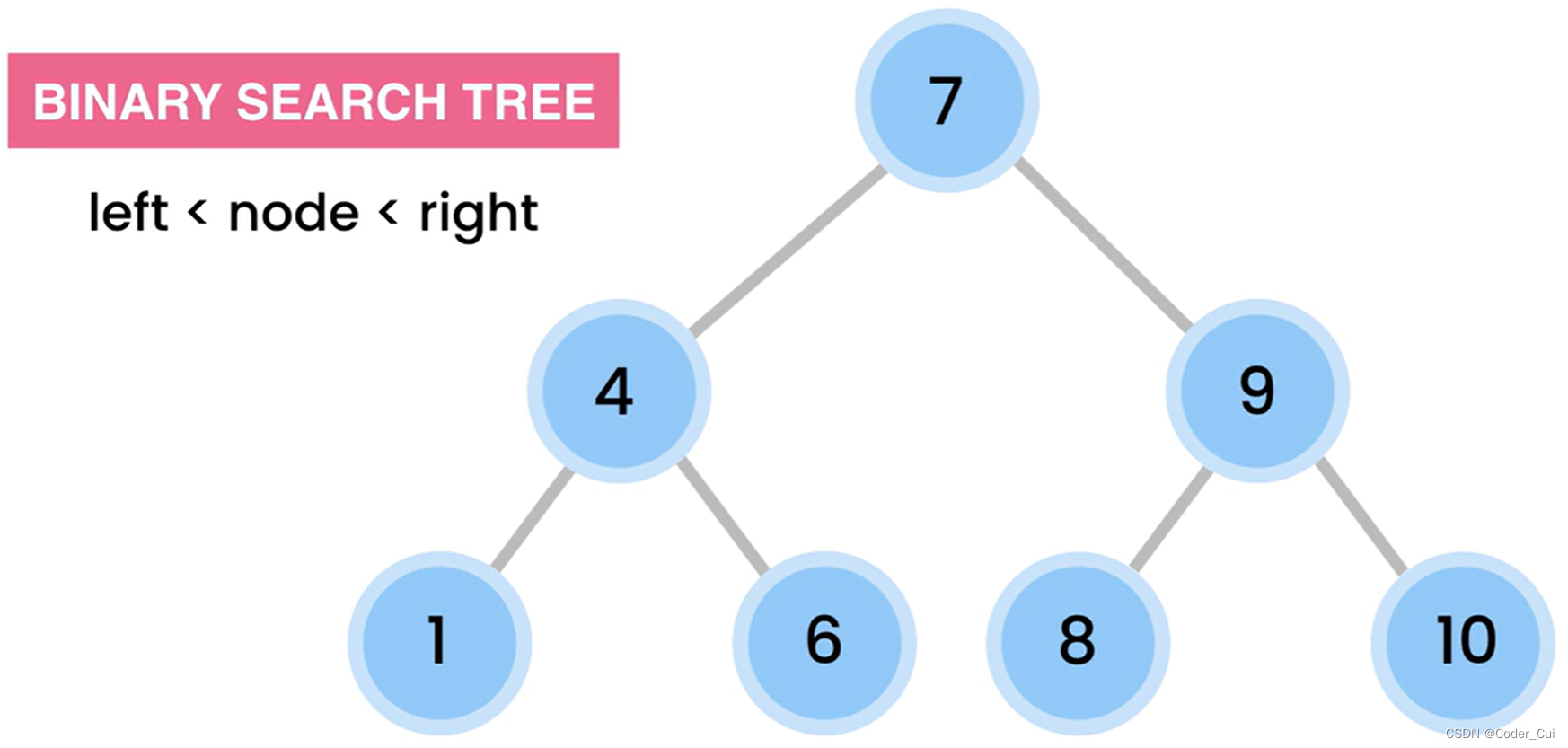
2.3.1 定义结点类Node
class Node{
int val;
Node left;
Node right;
public Node(int val){
this.val=val;
}
}
2.3.2 插入结点
思路:采用递归的方法实现
-
判断插入元素与根结点元素是否相同,相同时无需操作,不同时向下执行;
-
比根元素小往左边查找,若左结点不存在,则作为左结点插入即可;
-
比根元素大往右边查找,若右结点不存在,则作为右结点插入即可。
实现代码如下:
/**
* 添加元素
* @param val
*/
public void add(int val){
if(root==null){
root=new Node(val);
return;
}
addNode(val,root);
}
private void addNode(int val,Node root){
if(root==null || root.val==val){
return;
}
if(root.val>val){
if(root.left==null){
root.left=new Node(val);
}else {
addNode(val,root.left);
}
}else {
if(root.right==null){
root.right=new Node(val);
}else {
addNode(val,root.right);
}
}
}
2.3.3 查找结点
思路:采用递归的方法
1.判断与根节点是否相同,相同则返回true
2.比根元素小往左边查找,左节点为null则返回false表示不存在
3.比根元素大往右边查找,右节点为null则返回false表示不存在
实现代码如下:
/**
* 判断指定值是否存在
* @param val 指定值
* @return true--存在 false--不存在
*/
public boolean findVale(int val){
return isExit(root,val);
}
private boolean isExit(Node node,int val){
if(node==null){
return false;
}
if(node.val==val){
return true;
}else if(node.val>val){
return isExit(node.left,val);
}else {
return isExit(node.right,val);
}
}
2.3.4 删除结点
删除元素时要判断元素的情况:
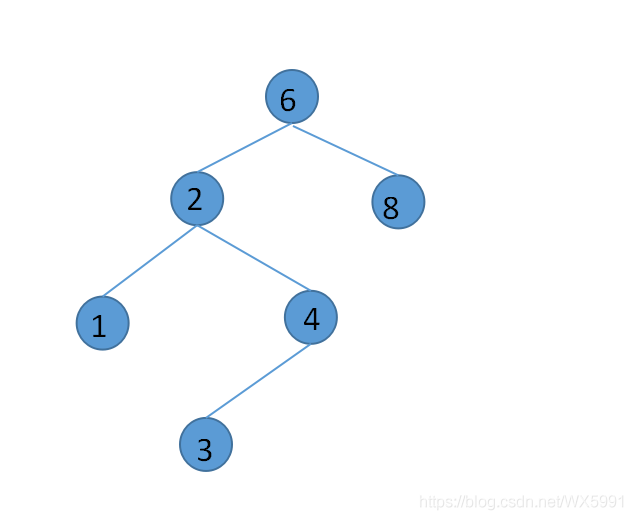
-
删除的元素没有叶子节点,直接删除,如删除值为1的节点,虽然平衡性不是太好,但是还是符合二叉查找树的特性
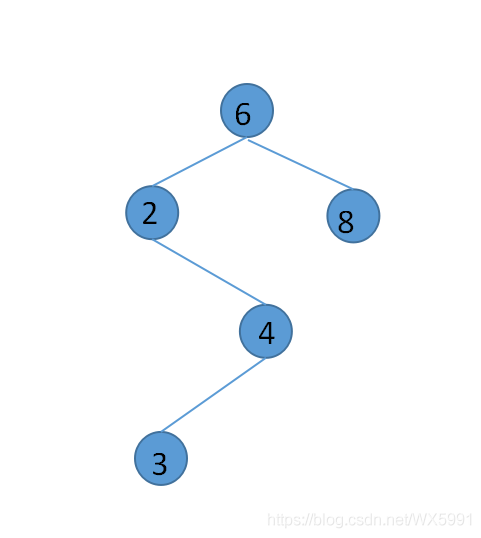
-
删除的元素只有一个节点,删除元素并将指针指向其子节点 ,如删除值为4的节点:
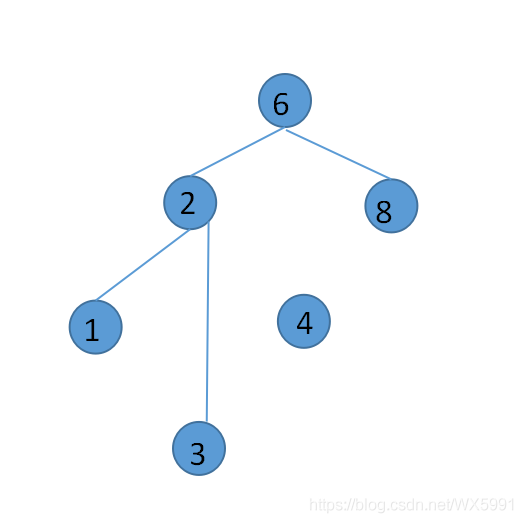
-
删除的元素有左右两个节点,从右节点中找出大于该节点的最小节点,作为新的节点A,如删除节点值为2的节点:
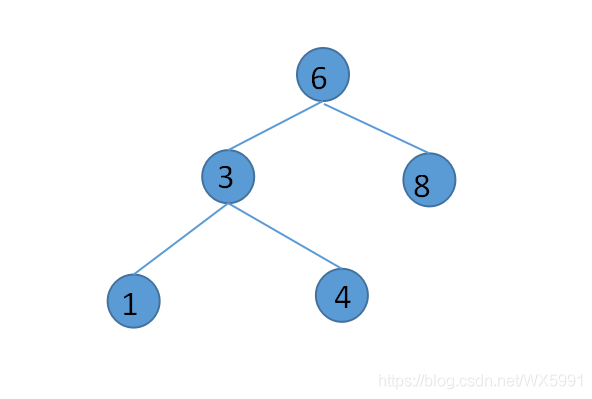
实现代码如下:
/**
* 删除元素
* 1.删除的元素没有叶子节点,直接删除
* 2.删除的元素只有一个节点,删除元素并将指针指向其子节点
* 3.删除的元素有两个节点,从右节点中找出大于该元素的最小值,作为新的节点
* @param val
*/
public void deleteElement(int val){
deleteElement(null,root,val,true);
}
/**
* 删除元素
* @param prev 父节点
* @param root 当前节点
* @param val 删除值
* @param isright 是否是右节点
*/
private void deleteElement(Node prev,Node root,int val,boolean isright){
if(root.val==val){
//删除的元素没有叶子节点,直接删除
if(root.left==null && root.right==null){
changeValue(prev,null,isright);
}else if(root.left!=null && root.right!=null){
//3.删除的元素有两个节点,从右节点中找出大于该元素的最小值,作为新的节点
changeValue(prev,new Node(findMinGt(root,root.right,true)),isright);
if(prev==null){
//对于头结点的删除特殊处理
prev=this.root;
prev.left=root.left;
prev.right=root.right;
return;
}
if(isright){
prev.right.right=root.right;
prev.right.left=root.left;
}else {
prev.left.right=root.right;
prev.left.left=root.left;
}
}//删除的元素只有一个节点,删除元素并将指针指向其子节点
else if(root.left!=null){
changeValue(prev,root.left,isright);
}else {
changeValue(prev,root.right,isright);
}
return;
}
if(root.val>val){
deleteElement(root,root.left,val,false);
}else{
deleteElement(root,root.right,val,true);
}
}
//改变元素值
private void changeValue(Node prev,Node value,boolean isright){
if(prev==null){
root=value;
return;
}
if(isright){
prev.right=value;
}else {
prev.left=value;
}
}
//寻找大于根节点的最小值
private int findMinGt(Node prev,Node root,boolean isRight){
if(root.left==null && root.right==null){
changeValue(prev,null,isRight);
return root.val;
}
if(root.left==null){
changeValue(prev,null,isRight);
return root.val;
}
return findMinGt(root,root.left,false);
}
2.3.5 实测
参考链接:2.2.7 Traversing Trees_哔哩哔哩_bilibili
-
定义结点、构造二叉查找树
package tree;
/**
* @ClassName BinaryTree
* @Description 定义一棵二叉查找树(二叉搜索树)ADT
* @Author Jiangnan Cui
* @Date 2022/10/16 11:27
* @Version 1.0
*/
public class BinaryTree {
// 定义根结点
private Node root;
// 插入元素实现1:递归实现
/**
* @MethodName addNode2
* @Description 插入元素
* @param: value
* @param: root
* @Author Jiangnan Cui
* @Date 13:24 2022/10/16
*/
public void addNode(int value){
// 初始化要插入的结点
Node node = new Node(value);
// 当根结点不存在时,数据直接插入根结点
if(root == null){
root = node;
return;
}
// 根结点存在时,继续向下进行遍历插入
addNode(value,root);
}
/**
* @MethodName addNode2
* @Description 在根节点存在的情况下插入元素
* @param: value
* @param: root
* @Author Jiangnan Cui
* @Date 14:02 2022/10/16
*/
private void addNode(int value,Node root){
// 当根结点不存在或者根结点的值等于插入值时,直接结束,无需操作,该操作的前提是根结点已存在
if(root == null || root.value == value){
return;
}
// 根结点存在的情况下,需要向下遍历进行插入,假定当前节点为根结点
Node current = root;
// 初始化要插入的结点
Node node = new Node(value);
// 根当前结点值与插入元素不相等时,要分别进行讨论
if(value < current.value){// 小于时,向左查找
if(current.leftChild == null){// 不存在时,直接插入左子结点
current.leftChild = node;
return;
}else{// 存在时,继续向下比较
// 更新当前结点
current = current.leftChild;
// 递归插入
addNode(value,current);
}
} else{// 大于时,向右查找
if(current.rightChild == null){// 不存在时,直接插入左子结点
current.rightChild = node;
}else{// 存在时,继续向下比较
// 更新当前结点
current = current.rightChild;
// 递归插入
addNode(value,current);
}
}
}
// 插入元素实现2:优化递归操作
/**
* @MethodName addNode
* @Description 插入元素
* @param: value 待插入元素
* @Author Jiangnan Cui
* @Date 11:32 2022/10/16
*/
public void addNode2(int value){
// 初始化要插入的结点
Node node = new Node(value);
// 根结点为空时
if(root == null){
// 初始化根结点
root = node;
return;
}
// 假设当前结点为根结点,即从根结点开始判断
Node current = root;
while (true){
// 插入值小于根结点的值,应放在左子树
if(value < current.value){
// 判断根结点的左孩子结点是否存在
if(current.leftChild == null){
// 不存在时初始化该结点
current.leftChild = node;
break;
}
// 更新当前结点
current = current.leftChild;
}else{// 插入值大于根结点的值,应放在右子树
if(current.rightChild == null){
current.rightChild = node;
break;
}
current = current.rightChild;
}
}
}
// 查找元素实现1:递归操作
/**
* @MethodName findNode
* @Description 查找数据在树中是否存在
* @param: value 待查找数据
* @return: boolean,其中,true表示存在,false表示不存在
* @Author Jiangnan Cui
* @Date 14:12 2022/10/16
*/
public boolean findNode(int value){
return findNode(value,root);
}
/**
* @MethodName findNode
* @Description 在根结点存在的前提下,查找数据在树中是否存在
* @param: value
* @param: root
* @return: boolean,其中,true表示存在,false表示不存在
* @Author Jiangnan Cui
* @Date 14:16 2022/10/16
*/
private boolean findNode(int value,Node root){
// 根结点不存在,直接结束
if(root == null){
return false;
}
// 假设当前结点current为根结点
Node current = root;
// 等于当前结点的值,说明找到了
if(value == current.value){
return true;
}else if(value < current.value){// 小于当前结点的值,要向左查找
// 更新当前结点
current = current.leftChild;
// 递归查找
return findNode(value,current);
}else {// 大于当前结点的值,要向右查找
// 更新当前结点
current = current.rightChild;
// 递归查找
return findNode(value,current);
}
}
// 查找元素实现2:优化递归操作
/**
* @MethodName findNode2
* @Description 查找数据在树中是否存在
* @param: value 待查找数据
* @return: boolean,其中,true表示存在,false表示不存在
* @Author Jiangnan Cui
* @Date 12:22 2022/10/16
*/
public boolean findNode2(int value){
// 假定当前结点为根结点,即从根结点开始判断
Node current = root;
// 当前结点不为null时执行
while (current != null){
// 查找值小于根结点的值,应在左子树进行查找
if(value < current.value){
// 更新当前结点
current = current.leftChild;
}else if(value > current.value){// 查找值大于根结点的值,应在右子树进行查找
current = current.rightChild;
}else{// 查找值等于根结点的值,表明找到
return true;
}
}
// 遍历完所有结点都不匹配时,说明不存在
return false;
}
// 删除元素实现1:递归操作
/**
* @MethodName deleteNode
* @Description 删除元素
* @param: value 待删除元素
* @Author Jiangnan Cui
* @Date 14:32 2022/10/16
*/
public void deleteNode(int value){
deleteNode(null,root,value,true);
}
/**
* @MethodName deleteNode
* @Description
* @param: parent 父结点
* @param: current 当前结点
* @param: value 删除值
* @param: isRight 是否是右结点
* @Author Jiangnan Cui
* @Date 14:35 2022/10/16
*/
private void deleteNode(Node parent,Node current,int value,boolean isRight){
// 当前结点的值等于删除元素
if(current.value == value){
// 当前结点没有孩子结点,即是一个叶子结点时,直接删除
if(current.leftChild == null && current.rightChild == null){
changeValue(parent,null,isRight);
}
// 当前结点有两个子节点,需要从右节点中找出大于该元素的最小值,作为新的当前结点
else if(current.leftChild != null && current.rightChild != null){
changeValue(parent,new Node(findMinGt(current,current.rightChild,true)),isRight);
// 对于头结点的删除特殊处理
if(parent == null){
parent = this.root;
parent.leftChild = current.leftChild;
parent.rightChild = current.rightChild;
return;
}
if(isRight){
parent.rightChild.rightChild = current.rightChild;
parent.rightChild.leftChild = current.leftChild;
}else {
parent.leftChild.rightChild = current.rightChild;
parent.leftChild.leftChild = current.leftChild;
}
}
// 当前结点只有一个孩子结点,删除元素并将指针指向其子节点
else if(current.leftChild != null){
changeValue(parent,current.leftChild,isRight);
}else {
changeValue(parent,current.rightChild,isRight);
}
return;
}
// 当前结点的值大于删除元素,向左递归遍历删除
else if(current.value > value){
deleteNode(root,root.leftChild,value,false);
}
// 当前结点的值小于删除元素,向右递归遍历删除
else{
deleteNode(root,root.rightChild,value,true);
}
}
/**
* @MethodName changeValue
* @Description 改变元素值
* @param: parent
* @param: node
* @param: isright
* @Author Jiangnan Cui
* @Date 14:41 2022/10/16
*/
private void changeValue(Node parent,Node current,boolean isRight){
if(parent == null){
root = current;
return;
}
if(isRight){
parent.rightChild = current;
}else {
parent.leftChild = current;
}
}
/**
* @MethodName findMinGt
* @Description 寻找大于根节点的最小值
* @param: parent
* @param: current
* @param: isRight
* @return: int
* @Author Jiangnan Cui
* @Date 15:20 2022/10/16
*/
private int findMinGt(Node parent,Node current,boolean isRight){
if(current.leftChild == null && current.rightChild == null){
changeValue(parent,null,isRight);
return current.value;
}
if(current.leftChild == null){
changeValue(parent,null,isRight);
return current.value;
}
return findMinGt(current,current.leftChild,false);
}
/**
* 定义树中结点
*/
private class Node {
/**
* 定义二叉树结点的数据域和指针域
*/
private int value; // 数据域,即结点中存储的值
private Node leftChild; // 左孩子结点 或 左孩子指针
private Node rightChild; // 右孩子结点 或 右孩子指针
/**
* 无参构造
*/
Node() {};
/**
* 有参构造
*
* @param value
*/
Node(int value) {
this.value = value;
}
/**
* 相关get、set方法
*/
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public Node getLeftChild() {
return leftChild;
}
public void setLeftChild(Node leftChild) {
this.leftChild = leftChild;
}
public Node getRightChild() {
return rightChild;
}
public void setRightChild(Node rightChild) {
this.rightChild = rightChild;
}
/**
* 重写toString方法
*
* @return
*/
@Override
public String toString() {
return "value=" + value;
}
}
}
-
测试
package tree;
import tree.Node;
/**
* @ClassName BinaryTreeTest
* @Description TODO
* @Author Jiangnan Cui
* @Date 2022/10/16 11:33
* @Version 1.0
*/
public class BinaryTreeTest {
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
// 插入结点
binaryTree.addNode(7);
binaryTree.addNode(4);
binaryTree.addNode(9);
binaryTree.addNode(1);
binaryTree.addNode(6);
binaryTree.addNode(8);
binaryTree.addNode(10);
System.out.println("Done");
// 查找结点
boolean isExists = binaryTree.findNode(9);
System.out.println("isExists = " + isExists);
isExists = binaryTree.findNode(5);
System.out.println("isExists = " + isExists);
System.out.println("--------------------------------------------------");
BinaryTree binaryTree2 = new BinaryTree();
// 插入结点
binaryTree2.addNode2(7);
binaryTree2.addNode2(4);
binaryTree2.addNode2(9);
binaryTree2.addNode2(1);
binaryTree2.addNode2(6);
binaryTree2.addNode2(8);
binaryTree2.addNode2(10);
System.out.println("Done");
// 查找结点
boolean isExists2 = binaryTree2.findNode2(9);
System.out.println("isExists2 = " + isExists2);
isExists2 = binaryTree2.findNode2(5);
System.out.println("isExists = " + isExists2);
// 删除结点
binaryTree2.deleteNode(7);
System.out.println("Done");
}
}
2.4 二叉树的遍历
2.4.1 定义
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中的所有结点,使得每个结点有且仅有被访问过一次。
-
深度优先遍历
-
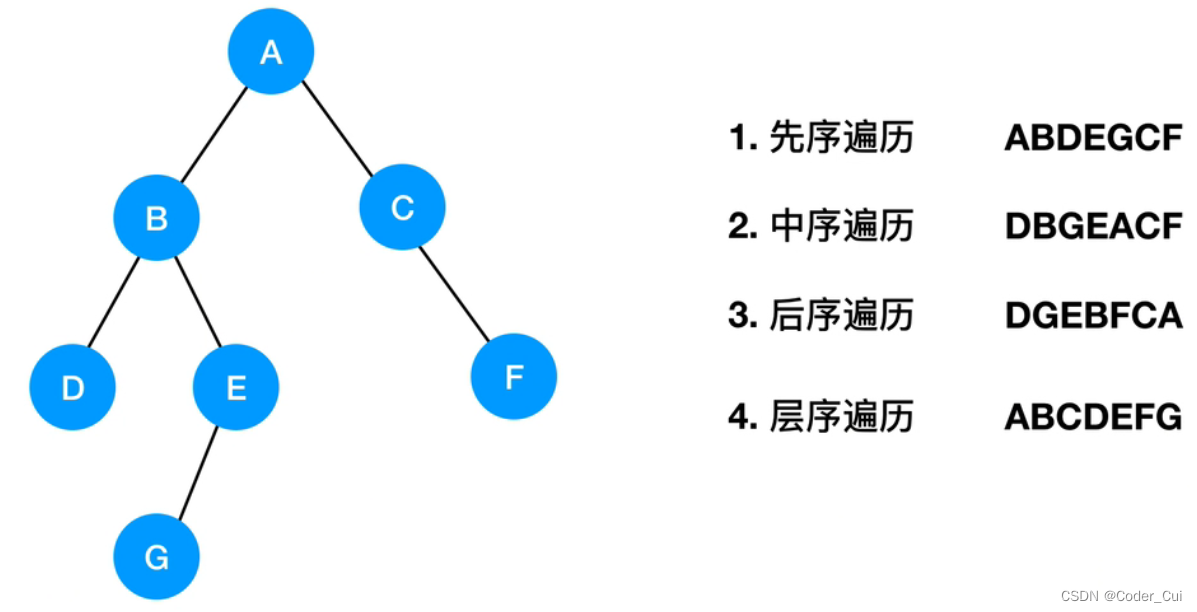
前序遍历:若二叉树为空,则返回空;若二叉树不为空,则先访问根结点,然后前序遍历左子树,最后前序遍历右子树(根-左-右)。
-
中序遍历:若二叉树为空,则返回空;若二叉树不为空,从根结点开始算起,先中序遍历根结点的左子树,然后中序遍历根结点,最后中序遍历右子树(左-根-右)。
-
后序遍历:若二叉树为空,则返回空;若二叉树不为空,从根结点开始算起,先后序遍历根结点的左子树,然后中序遍历根结点的右子树,最后中序遍历根结点(左-右-根)。
-
-
广度优先遍历
-
层序遍历:若二叉树为空,则返回空;若二叉树不为空,从根结点即树的第一层开始算起,从上到下逐层遍历,在同一层中,按照从左到右的顺序对接点进行逐个访问(层(从上到下)-结点(从左到右))。
-
2.4.2 Java代码实现
参考链接:java高频算法题(二叉树遍历)_哔哩哔哩_bilibili
package tree;
import java.util.*;
/**
* @ClassName TraverseBinaryTree
* @Description 遍历二叉树
* @Author Jiangnan Cui
* @Date 2022/10/16 21:05
* @Version 1.0
*/
public class TraverseBinaryTree {
/**
* 定义结点
*/
private static class Node{
String value;
Node left;
Node right;
Node(String value){
this.value = value;
}
}
/**
* 构建一棵简单的二叉树
* A
* B C
* D E F
* G
*/
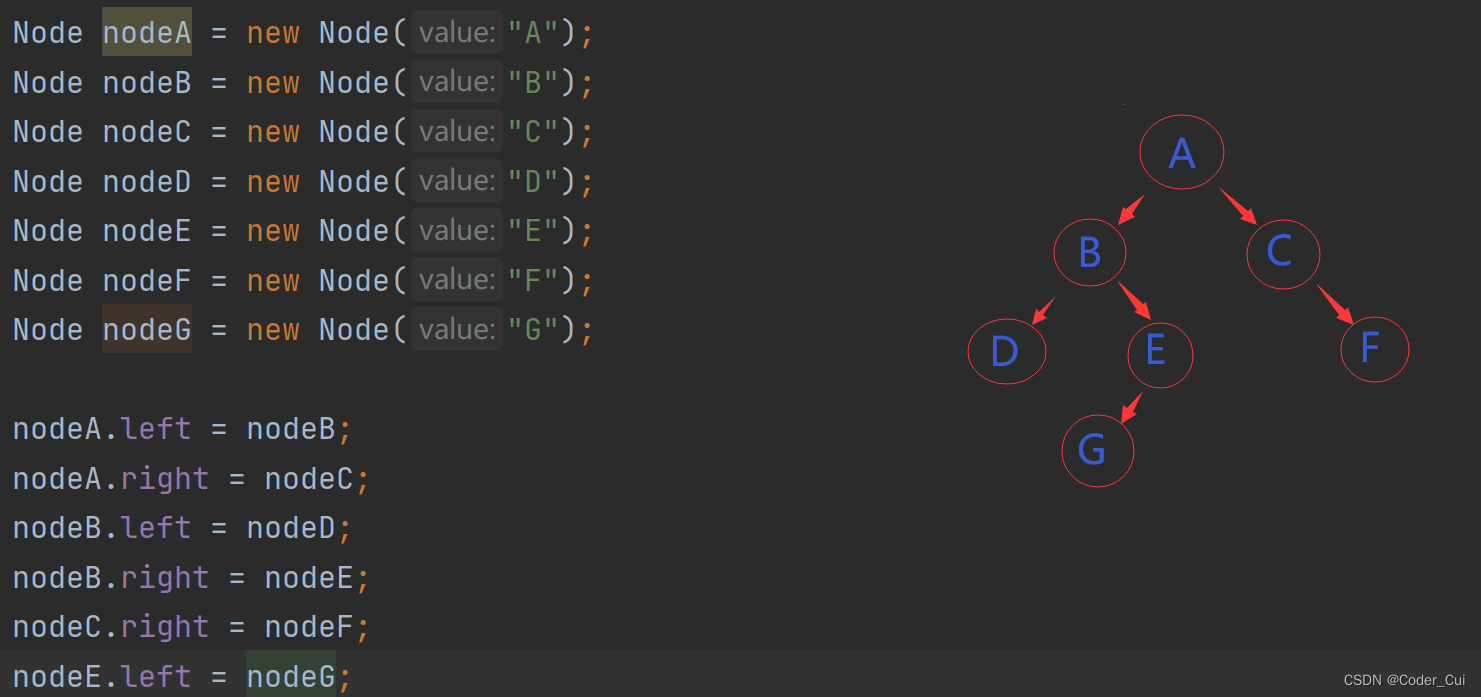
public static Node createBinaryTree(){
Node nodeA = new Node("A");
Node nodeB = new Node("B");
Node nodeC = new Node("C");
Node nodeD = new Node("D");
Node nodeE = new Node("E");
Node nodeF = new Node("F");
Node nodeG = new Node("G");
// 指定结点父子关系
nodeA.left = nodeB;
nodeA.right = nodeC;
nodeB.left = nodeD;
nodeB.right = nodeE;
nodeC.right = nodeF;
nodeE.left = nodeG;
return nodeA;
}
/**
* 2.前序遍历:根-左-右
*/
// 实现方式1:递归实现
public static void preOrderTraverse1(Node node){
if(node == null){
return;
}
System.out.print(node.value + " ");
preOrderTraverse1(node.left);
preOrderTraverse1(node.right);
}
// 实现方式2:非递归方式 栈实现:进栈右左根,出栈根左右
public static void preOrderTraverse2(Node node){
if(node == null){
return;
}
Stack<Node> stack = new Stack<>();
stack.push(node);
while(!stack.isEmpty()){
Node pop = stack.pop();
System.out.print(pop.value + " ");
if(pop.right != null){
stack.push(pop.right);
}
if(pop.left != null){
stack.push(pop.left);
}
}
}
/**
* 2.中序遍历:左-根-右
*/
// 实现方式1:递归实现
public static void inOrderTraverse1(Node node){
if(node == null){
return;
}
inOrderTraverse1(node.left);
System.out.print(node.value + " ");
inOrderTraverse1(node.right);
}
// 实现方式2:非递归方式 栈实现:进栈右根左,出栈左根右
public static void inOrderTraverse2(Node node){
if(node == null){
return;
}
Stack<Node> stack = new Stack<>();
Node cur = node;
while(!stack.isEmpty() || cur != null){
while(cur != null){
stack.push(cur);
cur = cur.left;
}
Node pop = stack.pop();
System.out.print(pop.value + " ");
if(pop.right != null){
cur = pop.right;
}
}
}
/**
* 3.后序遍历:左-右-根
*/
// 实现方式1:递归实现
public static void postOrderTraverse1(Node node){
if(node == null){
return;
}
postOrderTraverse1(node.left);
postOrderTraverse1(node.right);
System.out.print(node.value + " ");
}
// 实现方式2:非递归方式 栈实现:进栈根右左,出栈左右根 改造前序遍历
public static void postOrderTraverse2(Node node){
if(node == null){
return;
}
Stack<Node> stack = new Stack<>();
Stack<Node> stack2 = new Stack<>();
stack.push(node);
while(!stack.isEmpty()){
Node pop = stack.pop();
stack2.push(pop);
if(pop.left != null){
stack.push(pop.left);
}
if(pop.right != null){
stack.push(pop.right);
}
}
while(!stack2.isEmpty()){
System.out.print(stack2.pop().value + " ");
}
}
/**
* 4.层序遍历:直接输出元素
*/
public static void layerOrderTraverse(Node node){
if(node == null){
return;
}
Queue<Node> queue = new LinkedList<>();
queue.add(node);
while(!queue.isEmpty()){
Node poll = queue.poll();
System.out.print(poll.value + " ");
if(poll.left != null){
queue.add(poll.left);
}
if(poll.right != null){
queue.add(poll.right);
}
}
}
/**
* 层序遍历:按层输出
*/
public static List<List<String>> layerOrderTraverse2(Node node){
List<List<String>> res = new ArrayList<>();
Queue<Node> queue = new LinkedList<>();
queue.add(node);
List<String> temp;
while(!queue.isEmpty()){
int size = queue.size();
temp = new ArrayList<>();
while(size-- > 0){
Node poll = queue.poll();
temp.add(poll.value);
if(poll.left != null){
queue.add(poll.left);
}
if(poll.right != null){
queue.add(poll.right);
}
}
res.add(temp);
}
return res;
}
public static void main(String[] args) {
/**
* 构建一棵简单的二叉树
* A
* B C
* D E F
* G
*/
Node node = createBinaryTree();
System.out.println("前序遍历结果:根-左-右 递归实现");
preOrderTraverse1(node);// A B D E G C F
System.out.println();
System.out.println("前序遍历结果:根-左-右 栈实现");
preOrderTraverse2(node);// A B D E G C F
System.out.println();
System.out.println("中序遍历结果:左-根-右 递归实现");
inOrderTraverse1(node);// D B G E A C F
System.out.println();
System.out.println("中序遍历结果:左-根-右 栈实现");
inOrderTraverse2(node);// D B G E A C F
System.out.println();
System.out.println("后序遍历结果:左-右-根 递归实现");
postOrderTraverse1(node);// D G E B F C A
System.out.println();
System.out.println("后序遍历结果:左-右-根 栈实现");
postOrderTraverse2(node);// D G E B F C A
System.out.println();
System.out.println("层序遍历结果:从上到下,从左到右 队列实现 直接输出元素");
layerOrderTraverse(node);// A B C D E F G
System.out.println();
System.out.println("层序遍历结果:从上到下,从左到右 队列实现 按层输出");
System.out.println(layerOrderTraverse2(node));// [[A], [B, C], [D, E, F], [G]]
}
}
输出结果:
前序遍历结果:根-左-右 递归实现 A B D E G C F 前序遍历结果:根-左-右 栈实现 A B D E G C F 中序遍历结果:左-根-右 递归实现 D B G E A C F 中序遍历结果:左-根-右 栈实现 D B G E A C F 后序遍历结果:左-右-根 递归实现 D G E B F C A 后序遍历结果:左-右-根 栈实现 D G E B F C A 层序遍历结果:从上到下,从左到右 队列实现 直接输出元素 A B C D E F G 层序遍历结果:从上到下,从左到右 队列实现 按层输出 [[A], [B, C], [D, E, F], [G]]
待完善。。。。。。





















 1487
1487

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








