集成学习（中）task7

最新推荐文章于 2024-03-18 16:29:54 发布

原创最新推荐文章于 2024-03-18 16:29:54 发布 · 150 阅读

0 ·

CC 4.0 BY-SA版权

本文探讨了投票法在回归和分类问题中的应用，重点介绍了硬投票和软投票的区别，以及如何通过KNN模型的组合提高预测准确性。同时，Bagging方法通过多次采样训练独立模型，展示了其在减小模型方差上的优势，尤其是在高维小样本场景中的效果。

投票法

1.投票法分为回归类投票和分类型投票
2.其中分类型又分为硬投票和软投票
3.硬投票为直接可以选出来分到哪一类
4.软投票为概率加和最大的一类
5.回归投票为多个模型的平均值
6.投票法要求基模型之间不能差别太大，同时由于同质性，如果两个基模型之间的算法方式相近似，效果可能不大好，比如，如果两个模型分别为决策树和随机森林，均为树模型，可能效果并没有那么好

#建立数据集
from sklearn.datasets import make_classification
x,y=make_classification(n_samples=1000,n_features=20,n_informative=15,n_redundant=5,random_state=2)
print(x.shape,y.shape)
#使用多个KNN模型作为基模型演示投票法，其中每个模型采用不同的邻居值K参数
from sklearn.neighbors import KNeighborsClassifier
def get_voting():
    models=list()
    models.append(('knn1',KNeighborsClassifier(n_neighbors=1)))
    models.append(('knn3',KNeighborsClassifier(n_neighbors=3)))
    models.append(('knn5',KNeighborsClassifier(n_neighbors=5)))
    models.append(('knn7',KNeighborsClassifier(n_neighbors=7)))
    models.append(('knn9',KNeighborsClassifier(n_neighbors=9)))
    ensemble=VotingClassifier(estimators=models,voting='hard')
    return ensemble
#以创建一个模型列表来评估投票带来的提升
from sklearn.model_selection import RepeatedStratifiedKFold
def get_models():
    models=dict()
    models['knn1']=KNeighborsClassifier(n_neighbors=1)
    models['knn3']=KNeighborsClassifier(n_neighbors=3)
    models['knn5']=KNeighborsClassifier(n_neighbors=5)
    models['knn7']=KNeighborsClassifier(n_neighbors=7)
    models['knn9']=KNeighborsClassifier(n_neighbors=9)
    models['hard_voting']=get_voting()
    return models
#数接收一个模型实例，并以分层10倍交叉验证三次重复的分数列表的形式返回
from sklearn.model_selection import train_test_split,cross_val_score
def evaluate_model(model,x,y):
    cv=RepeatedStratifiedKFold(n_splits=10,n_repeats=3,random_state=1)
    scores=cross_val_score(model,x,y,scoring='accuracy',cv=cv,n_jobs=-1,error_score='raise')
    return scores
#可以报告每个算法的平均性能，还可以创建一个箱形图和须状图来比较每个算法的精度分数分布。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
#x,y=get_dataset()
models=get_models()
results,names=[],[]
for name,model in models.items():
    scores=evaluate_model(model,x,y)
    results.append(scores)
    names.append(name)
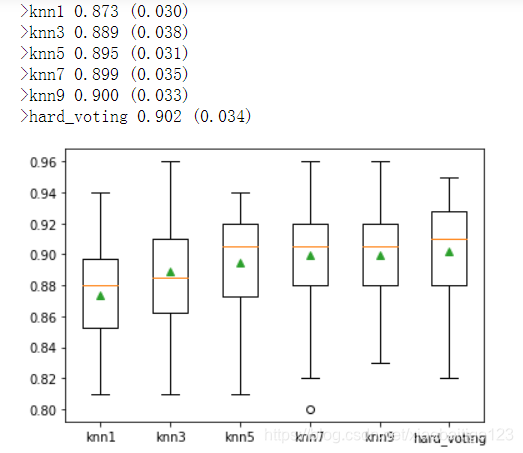
    print('>%s %.3f (%.3f)' % (name,np.mean(scores),np.std(scores)))
plt.boxplot(results,labels=names,showmeans=True)
plt.show()

结果如下图所示
在这里插入图片描述

Bagging

bagging的原理在于经过我们随机取出一个样本放入采样集合中，再把这个样本放回初始数据集，重复K次采样，最终我们可以获得一个大小为K的样本集合。同样的方法，我们可以采样出T个含K个样本的采样集合，然后基于每个采样集合训练出一个基学习器，再将这些基学习器进行结合。bagging的实在不同的训练集上进行的，也许训练集之间可能存在交集。不同的基模型在不同的训练集进行训练，最后将结果进行结合。其好处在于它在不剪枝决策树、神经网络等易受样本扰动的学习器上效果更加明显。在实际的使用中，加入列采样的Bagging技术对高维小样本往往有神奇的效果。

from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
model=BaggingClassifier()
cv=RepeatedStratifiedKFold(n_splits=10,n_repeats=3,random_state=1)
n_scores=cross_val_score(model,x,y,scoring='accuracy',cv=cv,n_jobs=-1,error_score='raise')
#cv=RepeatedStratifiedKFold(n_splits=10,n_repeats=3,random_state=1)
print('accuracy:%.3f (%.3f)'% (mean(n_scores),std(n_scores)))