数据结构 - 二叉树

二叉树

概念

二叉树是一种非常重要的数据结构，非常多其他数据结构都是基于二叉树的基础演变而来的。对于二叉树，有深度遍历和广度遍历，深度遍历有前序、中序以及后序三种遍历方法，广度遍历即我们寻常所说的层次遍历。由于树的定义本身就是递归定义，因此採用递归的方法去实现树的三种遍历不仅easy理解并且代码非常简洁，而对于广度遍历来说，须要其他数据结构的支撑。比方堆了。所以。对于一段代码来说，可读性有时候要比代码本身的效率要重要的多。

把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
(01) 每个节点有零个或多个子节点；
(02) 没有父节点的节点称为根节点；
(03) 每一个非根节点有且只有一个父节点；
(04) 除了根节点外，每个子节点可以分为多个不相交的子树。

四种基本的遍历思想

前序遍历：根结点 —> 左子树 —> 右子树
中序遍历：左子树—> 根结点 —> 右子树
后序遍历：左子树 —> 右子树 —> 根结点
层次遍历：仅仅需按层次遍历就可以
比如。求以下二叉树的各种遍历

前序遍历：1 2 4 5 7 8 3 6
中序遍历：4 2 7 5 8 1 3 6
后序遍历：4 7 8 5 2 6 3 1
层次遍历：1 2 3 4 5 6 7 8

树的基本术语

若一个结点有子树，那么该结点称为子树根的"双亲"，子树的根是该结点的"孩子"。有相同双亲的结点互为"兄弟"。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。

结点的度：结点拥有的子树的数目。
叶子：度为零的结点。
分支结点：度不为零的结点。
树的度：树中结点的最大的度。

层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1。树的高度：树中结点的最大层次。
无序树：如果树中结点的各子树之间的次序是不重要的，可以交换位置。有序树：如果树中结点的各子树之间的次序是重要的, 不可以交换位置。森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

二叉树的五种基本形态：

二叉树的性质

二叉树有以下几个性质：TODO(上标和下标)
性质1：二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。
性质2：深度为k的二叉树至多有2{k}-1个结点(k≥1)。
性质3：包含n个结点的二叉树的高度至少为log2 (n+1)。
性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1。

二叉树实现

from graphviz import Digraph
import uuid
from random import sample

# 二叉树类
class BTree(object):

    # 初始化
	def __init__(self, data=None, left=None, right=None):
		self.data = data    # 数据域
        	self.left = left    # 左子树
        	self.right = right  # 右子树
        	self.dot = Digraph(comment='Binary Tree'）
    
    # 前序遍历	
	def preorder(self):
		if self.data is not None:
			print(self.data,end=' ')
		if self.left is not None:
			print(self.left,end=' ')
        if self.right is not None:
            self.right.preorder()
    
   	# 中序遍历
   	def inorder(self):
   		if self.left is not None:
   			print(self.left,end=' ')
   		if self.data is not None:
   			print(self.data,end=' ')
   		if self.right is not None:
            	self.right.inorder()
    	# 后序遍历
    def postorder(self):
       	if self.left is not None:
            	self.left.postorder()
       	if self.right is not None:
            	self.right.postorder()
        	if self.data is not None:
            	print(self.data, end=' ')      
     
     # 层序遍历
   	def levelorder(self):
        	# 返回某个节点的左子树
        	def LChild_Of_Node(node):
            	return node.left if node.left is not None else None
        	# 返回某个节点的右子树
        	def RChild_Of_Node(node):
            	return node.right if node.right is not None else None
     
		# 层序遍历列表
		level_order = []
		# 是否添加根节点的数据
		if self.data is not None:
			level_order.append([self])
		
		#二叉树的高度
		height = self.height()
		if height >= 1:
			# 对第二层及其以后的层数进行操作, 在level_order中添加节点而不是数据
	     	for _ in range(2, height + 1):
              		level = []  # 该层的节点
              		for node in level_order[-1]:
                   		# 如果左孩子非空，则添加左孩子
              			if LChild_Of_Node(node):
                    		level.append(LChild_Of_Node(node))
                   		# 如果右孩子非空，则添加右孩子
                   		if RChild_Of_Node(node):
                        level.append(RChild_Of_Node(node))
              		# 如果该层非空，则添加该层
              		if level:
                   		level_order.append(level)
               	for i in range(0, height):  # 层数
               		for index in range(len(level_order[i])):
               			level_order[i][index] = level_order[i][index].data
               			
		return level_order
                
	#二叉树高度
	def height(self):
     	# 空的树高度为0, 只有root节点的树高度为1
		if self.data is None:
			return 0
		elif self.left is None and self.right is None:
			return 1
		# 根节点下只有一个分支
		elif self.left is None and self.right is not None:
			return 1+self.right.height()
		elif self.right is None and self.left is not None:
			return 1+self.left.height()
		else:
			return 1+max(self.left.height(),self.right.height())
	
	# 二叉树的叶子节点
    	def leaves(self):

	if self.data is None:
		return None
	elif self.left is None and self.right is None:
        	print(self.data, end=' ')
    	elif self.left is None and self.right is not None:
		self.right.leaves()
  	elif self.right is None and self.left is not None:
		self.left.leaves()
	else:
		self.left.leaves()
		self.right.leaves() 
		
	#二叉树可视化
	def print_tree(self, save_path='./Binary_Tree.gv', label=False):
     #略

上述实现的功能：
1.初始化方法：该树存放的数据为data,左子树，右子树为left和right，默认均为None;
2.preorder()方法：递归实现二叉树的先序遍历；
3.inorder()方法：递归实现二叉树的中序遍历；
4.postorder()方法：递归实现二叉树的后序遍历；
5.levelorder()方法：递归实现二叉树的层序遍历；
6.height()方法：计算二叉树的高度；
7.leaves()方法：计算二叉树的叶子结点；

实例二叉树

若我们需要实现图3的示例二叉树，完整的Python代码如下：

from Binary_Tree import BTree

# 构造二叉树, BOTTOM-UP METHOD
right_tree = BTree(6)
right_tree.left = BTree(2)
right_tree.right = BTree(4)

left_tree = BTree(5)
left_tree.left = BTree(1)
left_tree.right = BTree(3)

tree = BTree(11)
tree.left = left_tree
tree.right = right_tree

left_tree = BTree(7)
left_tree.left = BTree(3)
left_tree.right = BTree(4)

right_tree = tree # 增加新的变量
tree = BTree(18)
tree.left = left_tree
tree.right = right_tree

print('先序遍历为:')
tree.preorder()
print()

print('中序遍历为:')
tree.inorder()
print()

print('后序遍历为:')
tree.postorder()
print()

print('层序遍历为:')
level_order = tree.levelorder()
print(level_order)
print()

height = tree.height()
print('树的高度为%s.' % height)

print('叶子节点为：')
tree.leaves()
print()

# 利用Graphviz进行二叉树的可视化
tree.print_tree(save_path='E://BTree.gv', label=True)

输出结果如下

先序遍历为:
18 7 3 4 11 5 1 3 6 2 4 
中序遍历为:
3 7 4 18 1 5 3 11 2 6 4 
后序遍历为:
3 4 7 1 3 5 2 4 6 11 18 
层序遍历为:
[[18], [7, 11], [3, 4, 5, 6], [1, 3, 2, 4]]

树的高度为4.
叶子节点为：
3 4 1 3 2 4 

可视结果

总结
二叉树是很多重要算法及模型的基础，比如二叉搜索树（BST），哈夫曼树(Huffman Tree)，CART决策树等。
在Python中，已有别人实现好的二叉树的模块，它是binarytree模块，其官方文档的网址为：https://pypi.org/project/binarytree/。其使用的例子如下：

遍历方法：

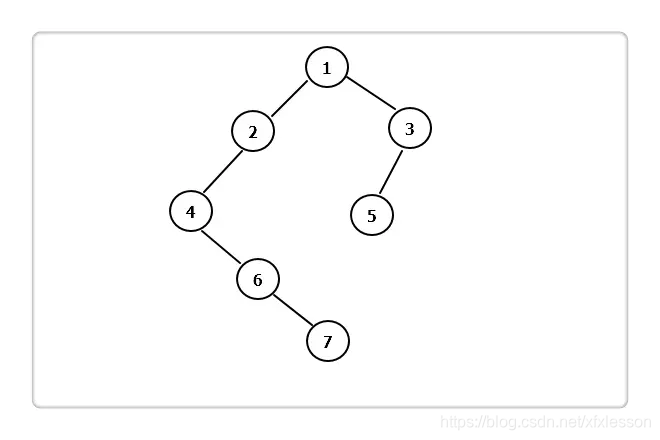
1.前序遍历

对于当前节点，先输出该节点，然后输出他的左孩子，最后输出他的右孩子。以上图为例，递归的过程如下：
（1）：输出 1，接着左孩子；
（2）：输出 2，接着左孩子；
（3）：输出 4，左孩子为空，再接着右孩子；
（4）：输出 6，左孩子为空，再接着右孩子；
（5）：输出 7，左右孩子都为空，此时 2 的左子树全部输出，2 的右子树为空，此时 1 的左子树全部输出，接着 1 的右子树；
（6）：输出 3，接着左孩子；
（7）：输出 5，左右孩子为空，此时 3 的左子树全部输出，3 的右子树为空，至此 1 的右子树全部输出，结束。

2.中序遍历

对于当前结点，先输出它的左孩子，然后输出该结点，最后输出它的右孩子。以上图为例：
（1）：1–>2–>4，4 的左孩子为空，输出 4，接着右孩子；
（2）：6 的左孩子为空，输出 6，接着右孩子；
（3）：7 的左孩子为空，输出 7，右孩子也为空，此时 2 的左子树全部输出，输出 2，2 的右孩子为空，此时 1 的左子树全部输出，输出 1，接着 1 的右孩子；
（4）：3–>5，5 左孩子为空，输出 5，右孩子也为空，此时 3 的左子树全部输出，而 3 的右孩子为空，至此 1 的右子树全部输出，结束。

3.后序遍历

对于当前结点，先输出它的左孩子，然后输出它的右孩子，最后输出该结点。依旧以上图为例：
（1）：1->2->4->6->7，7 无左孩子，也无右孩子，输出 7，此时 6 无左孩子，而 6 的右子树也全部输出，输出 6，此时 4 无左子树，而 4 的右子树全部输出，输出 4，此时 2 的左子树全部输出，且 2 无右子树，输出 2，此时 1 的左子树全部输出，接着转向右子树；
（2）：3->5，5 无左孩子，也无右孩子，输出 5，此时 3 的左子树全部输出，且 3 无右孩子，输出 3，此时 1 的右子树全部输出，输出 1，结束。

4.根据前序遍历中序遍历推导树的结构

已知：
前序遍历: GDAFEMHZ
中序遍历: ADEFGHMZ
求后序遍历
首先，要先画出这棵二叉树，怎么画呢？根据上面说的我们一步一步来……
1.先看前序遍历，前序遍历第一个一定是根节点，那么我们可以知道，这棵树的根节点是G，接着，我们看中序遍历中，根节点一定是在中间访问的，那么既然知道了G是根节点，则在中序遍历中找到G的位置，G的左边一定就是这棵树的左子树，G的右边就是这棵树的右子树了。
2.我们根据第一步的分析，大致应该知道左子树节点有：ADEF，右子树的节点有：HMZ。同时，这个也分别是左子树和右子树的中序遍历的序列。
3.在前序遍历遍历完根节点后，接着执行前序遍历左子树，注意，是前序遍历，什么意思？就是把左子树当成一棵独立的树，执行前序遍历，同样先访问左子树的根，由此可以得到，左子树的根是D，第2步我们已经知道左子树是ADEF了，那么在这一步得到左子树的根是D，请看第4步。
4.从第2步得到的中序遍历的节点序列中，找到D，发现D左边只有一个A，说明D的左子树只有一个叶子节点，D的右边呢？我们可以得到D的右子树有EF，再看前序遍历的序列，发现F在前，也就是说，F是先前序遍历访问的，则得到E是F的左子树，只有一个叶子节点。
5.到这里，我们可以得到这棵树的根节点和左子树的结构了。如下图：

6.接着看右子树，在第2步的右子树中序遍历序列中，右子树是HMZ三个节点，那么先看前序遍历的序列，先出现的是M，那么M就是右子树的根节点，刚好，HZ在M的左右，分别是它的左子树和右子树，因此，右子树的结构就出来了：

7.到这里，我们可以得到整棵树的结构：

5.根据树的中序遍历后序遍历推导树的结构

中序遍历：ADEFGHMZ
后序遍历：AEFDHZMG

1.根据后序遍历的特点（左右中），根节点在结尾，确定G是根节点。根据中序遍历的特点（左中右），确定ADEF组成左子树，HMZ组成右子树。

2.分析左子树。ADEF这四个元素在后序遍历（左右中）中的顺序是AEFD，在中序遍历（左中右）中的顺序是ADEF。根据后序遍历（左右中）的特点确定D是左子树的节点，根据中序遍历（左中右）的特点发现A在D前面，所以A是左子树的左叶子，EF则是左子树的右分枝。
EF在后序（左右中）和中序（左中右）的相对位置是一样的，所以EF关系是左右或者左中，排除左右关系（缺乏节点），所以EF关系是左中。

3.分析右子树。HMZ这三个元素在中序遍历（左中右）的顺序是HMZ，在后序遍历（左右中）的顺序是HZM。根据后序遍历（左右中）的特点，M在尾部，即M是右子树的节点。再根据中序遍历（左中右）的特点，确定H（M的前面）是右子树的左叶子，Z（M的后面）是右子树的右叶子。

所以右子树的形状

4.最后得出整棵树的形状

6.思路

存在中序遍历条件时候，可以找到根节点划分左右根支（前序遍历的头是根节点，后序遍历的尾是根节点）。即：
中序遍历划分为 [ 左子树 | 根节点 | 右子树 ]
前序遍历划分为 [ 根节点 | 左子树 | 右子树 ]
自此可确定 三个节点的关系 ：
1.树的根节点、2.左子树根节点、3.右子树根节点（即前序遍历中左（右）子树的首个元素）