用lru_cache提高性能

最新推荐文章于 2025-06-14 14:42:52 发布

原创最新推荐文章于 2025-06-14 14:42:52 发布 · 4.4k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#lru_cache #leetcode #组合总数

笔记同时被 2 个专栏收录

15 篇文章

订阅专栏

Python

2 篇文章

订阅专栏

本文探讨了lru_cache在动态规划中的应用，通过对比不同算法解决LeetCode题目，如爬楼梯和组合总和IV，展示了lru_cache如何优化递归函数的性能，同时也讨论了递归深度限制的问题及解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

leetcode 上有一题爬楼梯的题，一个n阶的台阶，每次可爬1阶或2阶，问有多少中爬法。这道题不难，就是一个斐波那契数列。我用循环写的，没啥问题。然后看评论里有人用递归写，说会超时。然后有人用了lru_cache装饰器来提高性能，顺利通过。

lru即least recently used，lru_cache可以记录函数的调用结果，再次使用时直接使用之前的返回值，而不真的再次调用。
注意，被lru_cache装饰的函数，其参数必须是可哈希的

from functools import lru_cache
import time

@lru_cache(maxsize=5)
def a(i):
    print(i)

t=time.time()
for i in [1,2,3,4,5]*1000:
    a(i)
t=time.time()-t
print(t)

以上程序输出为：
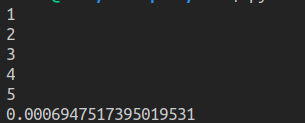
在这里插入图片描述
可以看到，a(i)实际只执行了5次。lru_cache 的参数maxsize 代表能缓存几个函数执行的结果。

lru_cache容易让人联想到带备忘的动态规划，有了lru_cache，岂不是可以直接写普通的递归函数来达到类似动态规划的效果了？事实是，有时候还是要注意的！

比如，leetcode 第377题“组合总和IV”:
在这里插入图片描述
由于“组合总和”前几题都是用回溯法，这道题我一开始也用回溯法做的：

class Solution:
    def __init__(self):
        self.res = 0
        self.target = 0
        self.temp = []

    def backTrace(self, cans):
        s = sum(self.temp)
        for x in cans:
            if s+x == self.target:
                self.temp.append(x)
                self.res += 1  
                self.temp.pop()
            elif s+x < self.target:
                self.temp.append(x)
                self.backTrace(cans)
                self.temp.pop()
            else:
                break
        
    def combinationSum4(self, candidates, target):
        candidates.sort()
        self.target = target
        self.backTrace(candidates)
        return self.res

然而超时了。。。那么就用动态规划吧。想到lru_cache，我就自顶向下直接递归了：

from functools import lru_cache

class Solution:
 @lru_cache()
 def combinationSum(self, candidates, target):
     if len(candidates)==0:
         return 0
     if target == 0:
         return 1
     if target < min(candidates):
         return 0
     r = 0
     for x in candidates:
         r += self.combinationSum(candidates,target-x)
     return r
 
 def combinationSum4(self, candidates, target):
         cans = tuple(candidates)
         return self.combinationSum(cans, target)

然而还是超时了。。。在自己电脑上跑了下，提示“RecursionError: maximum recursion depth exceeded in comparison”，原来是超过最大递归层数了。。。。查了下最后的测试用例，candidates=[3,33,333],target=10000,确实递归层数太深了。所以还是老老实实自己写了自底向上的动态规划算法：

class Solution:
    def combinationSum4(self, candidates, target):
        men = [0]*(target+1)
        for i in range(target+1):
            if i in candidates:
                men[i] += 1
            for x in candidates:
                if i - x >= 0:
                    men[i] += men[i-x]
        return men[target]