Daily AI 20251126 (注意力机制)

参考资料：神经网络与深度学习

内容概览（Nano Banana Pro）：

注意力

聚焦式注意力：自上而下的有意识的注意力，有预定目的、依赖任务的，主动有意识地聚焦于某一对象的注意力

基于显著性的注意力：由外界刺激驱动的的注意，不需主动干预，与任务无关

鸡尾酒会效应：

'''
当一个人在吵闹的鸡尾酒会上和朋友聊天时，尽管周围噪音干扰很多，他还是可以听到朋友的谈话内容，而忽略其他人的声音（聚焦式注意力）。
同时，如果未注意到的背景声中有重要的词（比如他的名字），他会马上注意到（显著性注意力）
'''

ANN中的注意力机制

当用神经网络来处理大量的输入信息时，也可以借鉴人脑的注意力机制，只选择一些关键的信息输入进行处理，来提高神经网络的效率 (如max pooling, gating)

用 $X=\left[{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N\right]$ 表示 $N$ 组输入信息，其中每个向量 ${\mathbf{x}}_i,i\in [1,N]$ 都表示一组输入信息。为了节省计算资源，不需要将所有信息都输入到神经网络，只需要从 $X$ 中选择一些和任务相关的信息。

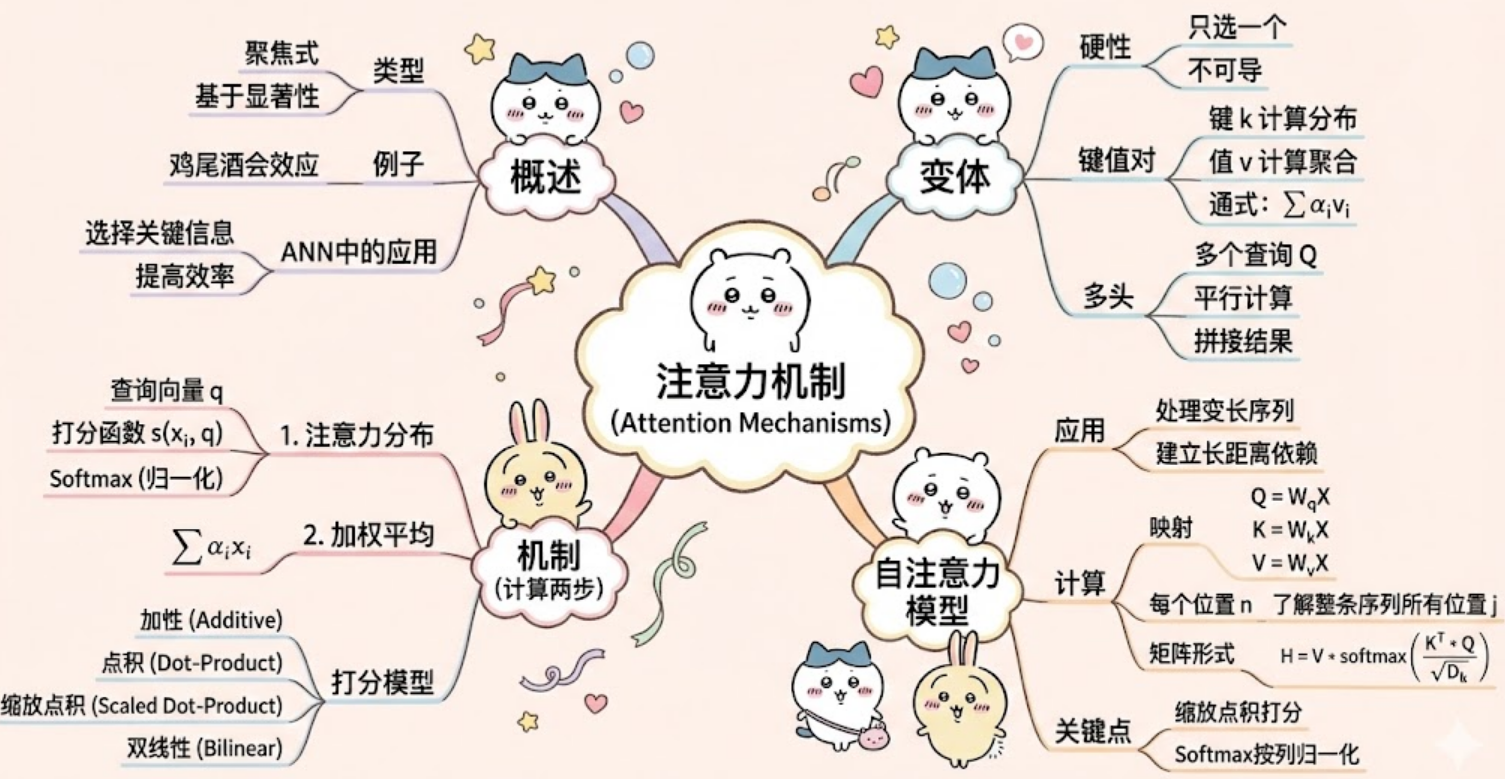
注意力机制的计算可以分为两步：一是在所有输入信息上计算注意力分布，二是根据注意力分布来计算输入信息的加权平均。

• 注意力分布：为了从 $N$ 个输入向量 $\left[{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N\right]$ 中选择出和某个特定任务相关的信息，通过引入一个和任务相关的表示$\mathbf{q}$，称为查询向量（Query Vector, $\mathbf{q}$），并通过一个打分函数$s({\mathbf{x}}_i,\mathbf{q})$来计算每个输入向量${\mathbf{x}}_i$和查询向量$\mathbf{q}$之间的相关性
  给定查询向量$\mathbf{q}$，用注意力变量 $z\in [1,N]$ 来表示被选择信息的索引位置，即 $z=i$ 表示选择了第 $i$ 个输入向量。则可以得到，在给定 $\mathbf{q}$ 和 $X=\left[{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N\right]$ 下，选择第 $i$ 个输入向量 ${\mathbf{x}}_i$的概率 ${\alpha }_i$：
  $$\begin{array}{rl}{\alpha }_i& =p(z=i\mid X,\mathbf{q})\\ & =\mathrm{softmax}\left(s\left({\mathbf{x}}_i,\mathbf{q}\right)\right)\\ & =\frac{\exp \left(s\left({\mathbf{x}}_i,\mathbf{q}\right)\right)}{{\sum }_{j=1}^N\exp \left(s\left({\mathbf{x}}_j,\mathbf{q}\right)\right)},\end{array}$$
  其中，${\alpha }_i=p(z=i\mid X,\mathbf{q})$ 为注意力分布（Attention Distribution），描述了第$i$个输入向量受关注的程度。
  注意力打分函数$s\left({\mathbf{x}}_i,\mathbf{q}\right)$ 可以使用以下几种方式来计算：

  –加性模型
  $$s\left({\mathbf{x}}_i,\mathbf{q}\right)={\mathbf{v}}^{\mathrm{T}}\tanh \left(W{\mathbf{x}}_i+U\mathbf{q}\right),$$
  –点积模型
  $$s\left({\mathbf{x}}_i,\mathbf{q}\right)={\mathbf{x}}_i^{\mathrm{T}}\mathbf{q},$$
  –缩放点积模型
  $$s\left({\mathbf{x}}_i,\mathbf{q}\right)=\frac{{\mathbf{x}}_i^{\mathrm{T}}\mathbf{q}}{\sqrt{d}},$$
  –双线性模型
  $$s\left({\mathbf{x}}_i,\mathbf{q}\right)={\mathbf{x}}_i^{\mathrm{T}}W\mathbf{q},$$

• 根据注意力分布计算输入信息的加权平均：
  $$\begin{array}{rl}\text{软性注意力机制：}\mathrm{att}(X,\mathbf{q})& =\sum _{i=1}^N{\alpha }_i{\mathbf{x}}_i={\mathbb{E}}_{z\sim p(z\mid X,\mathbf{q})}\left[{\mathbf{x}}_z\right].\end{array}$$
  

注意力机制变体

硬性注意力

只关注某一个输入向量，如
$$\mathrm{att}(X,\mathbf{q})={\mathbf{x}}_j,j=\underset{i=1}{\arg \stackrel{N}{\max }}{\alpha }_i$$
其主要缺点是基于最大采样或随机采样的方式来选择信息，使得最终的损失函数与注意力分布之间的函数关系不可导，因此无法使用反向传播算法进行训练

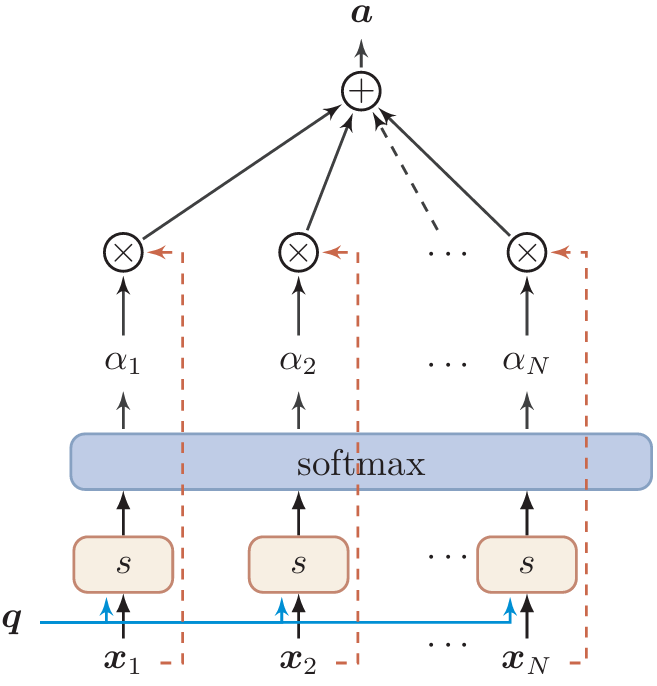
键值对注意力

用键值对（key-value pair, $\mathbf{k}$, $\mathbf{v}$）格式来表示输入信息，其中 ＂键$\mathbf{k}$＂用来计算注意力分布 ${\alpha }_i$ ，＂值$\mathbf{v}$＂用来计算聚合信息。
用 $(K,V)=\left[\left({\mathbf{k}}_1,{\mathbf{v}}_1\right),\cdots ,\left({\mathbf{k}}_N,{\mathbf{v}}_N\right)\right]$ 表示 $N$ 组输入信息（类比于$X=\left[{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N\right]$），给定任务相关的查询向量 $\mathbf{q}$ 时，注意力函数为
$$\begin{array}{rl}\mathrm{att}((K,V),\mathbf{q})& =\sum _{i=1}^N{\alpha }_i{\mathbf{v}}_i\\ & =\sum _{i=1}^N\frac{\exp \left(s\left({\mathbf{k}}_i,\mathbf{q}\right)\right)}{{\sum }_j\exp \left(s\left({\mathbf{k}}_j,\mathbf{q}\right)\right)}{\mathbf{v}}_i\end{array}$$
其中 $s\left({\mathbf{k}}_i,\mathbf{q}\right)$ 为打分函数，键值对注意力将前述的输入$X$一般化为K&V；当$K=V$时，其退化为普通注意力机制。

多头注意力

在键值对注意力的基础上，多头注意力（Multi－Head Attention）是利用多个查询 $Q=\left[{\mathbf{q}}_1,\cdots ,{\mathbf{q}}_M\right]$ ，来平行地计算从输入信息中选取多组信息。每个注意力关注输入信息的不同部分，将得到的各个结果${\mathbf{a}}_i$进行向量拼接
$$\mathrm{att}((K,V),Q)=\mathrm{att}\left((K,V),{\mathbf{q}}_1\right)\oplus \cdots \oplus \mathrm{att}\left((K,V),{\mathbf{q}}_M\right),$$

注意力机制应用

当使用神经网络来处理一个变长的向量序列时，通常可以使用卷积网络或循环网络进行编码来得到一个相同长度的输出向量序列；（但往往只能建模输入信息的局部依赖关系）。

为建立变长输入向量序列的长距离依赖关系，

自注意力模型

假设输入序列为 $\mathbf{X}=\left[{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N\right]\in {\mathbb{R}}^{D_x\times N}$ ，输出序列为 $\mathbf{H}=\left[{\mathbf{h}}_1,\cdots ,{\mathbf{h}}_N\right]\in {\mathbb{R}}^{D_v\times N}$ ，自注意力模型的具体计算过程如下：
（1）对于每个输入 ${\mathbf{x}}_i$ ，我们首先将其线性映射到三个不同的空间，得到查询向量 ${\mathbf{q}}_i\in {\mathbb{R}}^{D_k}$ 、键向量 ${\mathbf{k}}_i\in {\mathbb{R}}^{D_k}$ 和值向量 ${\mathbf{v}}_i\in {\mathbb{R}}^{D_v}$ 。

对于整个输入序列 $\mathbf{X}$ ，线性映射过程可以简写为

$$\begin{array}{rl}\mathbf{Q}& ={\mathbf{W}}_q\mathbf{X}\in {\mathbb{R}}^{D_k\times N},\\ \mathbf{K}& ={\mathbf{W}}_k\mathbf{X}\in {\mathbb{R}}^{D_k\times N},\\ \mathbf{V}& ={\mathbf{W}}_v\mathbf{X}\in {\mathbb{R}}^{D_v\times N},\end{array}$$
其中 ${\mathbf{W}}_q\in {\mathbb{R}}^{D_k\times D_x},{\mathbf{W}}_k\in {\mathbb{R}}^{D_k\times D_x},{\mathbf{W}}_v\in {\mathbb{R}}^{D_v\times D_x}$ 分别为线性映射的参数矩阵， $\mathbf{Q}=\left[{\mathbf{q}}_1,\cdots ,{\mathbf{q}}_N\right],\mathbf{K}=\left[{\mathbf{k}}_1,\cdots ,{\mathbf{k}}_N\right],\mathbf{V}=\left[{\mathbf{v}}_1,\cdots ,{\mathbf{v}}_N\right]$ 分别是由查询向量、键向量和值向量构成的矩阵．

对于每一个查询向量 ${\mathbf{q}}_n\in \mathbf{Q}$ ，基于前述键值对注意力机制计算方式（$\mathrm{att}((K,V),\mathbf{q})={\sum }_{i=1}^N{\alpha }_i{\mathbf{v}}_i={\sum }_{i=1}^N\frac{\exp \left(s\left({\mathbf{k}}_i,\mathbf{q}\right)\right)}{{\sum }_j\exp \left(s\left({\mathbf{k}}_j,\mathbf{q}\right)\right)}{\mathbf{v}}_i$），可以得到输出向量 ${\mathbf{h}}_n$：
$$\begin{array}{rl}& {\mathbf{h}}_n=\mathrm{att}\left((\mathbf{K},\mathbf{V}),{\mathbf{q}}_n\right)\\ & =\sum _{j=1}^N{\alpha }_{nj}{\mathbf{v}}_j\\ & =\sum _{j=1}^N\mathrm{softmax}\left(s\left({\mathbf{k}}_j,{\mathbf{q}}_n\right)\right){\mathbf{v}}_j,\end{array}$$
对于序列里每个位置 $n$ ，都让它了解＂整条序列里所有位置 $j$＂的内容 $x_j$ ，算一个权重 ${\alpha }_{nj}$ ，然后把这些 $x_j$ 的值向量加权求和，得到输出 $h_n$ 。
其中 $n,j\in [1,N]$ 为输出和输入向量序列的位置，${\alpha }_{nj}$ 表示第 $n$ 个输出关注到第 $j$个输入的权重。
注意到，$k_j\in {\mathbb{R}}^{D_k\times 1}$, $q_n\in {\mathbb{R}}^{D_k\times 1}$, $v_j\in {\mathbb{R}}^{D_v\times 1}$, $h_n\in {\mathbb{R}}^{D_v\times 1}$，若使用点积（$k_j^T{q}_n\in {\mathbb{R}}^{1\times 1}$）

如果使用缩放点积（$s\left({\mathbf{k}}_i,\mathbf{q}\right)=\frac{{\mathbf{k}}_i^{\mathrm{T}}\mathbf{q}}{\sqrt{d}}$）来作为注意力打分函数，输出向量序列可以简写为
$$\mathbf{H}=\mathbf{V}\text{ softmax }\left(\frac{{\mathbf{K}}^{\top }\mathbf{Q}}{\sqrt{D_k}}\right)\in {\mathbb{R}}^{D_v\times N}$$
其中，注意到$\frac{{\mathbf{K}}^{\top }\mathbf{Q}}{\sqrt{D_k}}\in {\mathbb{R}}^{N\times N}$，$\mathrm{softmax}(\cdot )$ 为按列进行归一化的函数。

自注意力基于向量形式的推导整理

$总体上：$

• 选定输入序列的任一位置$n$，其对应的查询向量为$q_n=W_q{x}_n\in {\mathbb{R}}^{D_k}$
• 随后，用得到的查询向量$q_n$，去"query"所有位置的键向量 { k j = W k x j ∈ R D k } j \{k_j = W_k x_j \in \mathbb{R}^{D_k} \}_j {kj​=Wk​xj​∈RDk​}j​，基于 缩放点积模型+softmax 得到对于每个值向量 { v j = W v x j ∈ R D v } j \{v_j = W_v x_j \in \mathbb{R}^{D_v} \}_j {vj​=Wv​xj​∈RDv​}j​的权重 { α n j } j \{ \alpha_{nj} \}_j {αnj​}j​
• 最后，加权求和得到对应的位置n的输出向量$h_n\in {\mathbb{R}}^{D_v}$

$更具体而言：$

• 打分函数采用缩放点积$s\left({\mathbf{x}}_i,\mathbf{q}\right)=\frac{{\mathbf{x}}_i^{\mathrm{T}}\mathbf{q}}{\sqrt{d}}$，得到
  $$s\left(k_j,q_n\right)=\frac{k_j^{\top }{q}_n}{\sqrt{D_k}}\in \mathbb{R}$$
  对于所有位置j，得到分数向量
  $$s^{(n)}=\frac{1}{\sqrt{D_k}}{K}^{\top }{q}_n=\left[\begin{array}{c}s\left(k_1,q_n\right)\\ ⋮\\ s\left(k_N,q_n\right)\end{array}\right]\in {\mathbb{R}}^N$$
• 为得到权重向量，对 $s^{(n)}$ 做 softmax
  $${\alpha }_n=\mathrm{softmax}\left(s^{(n)}\right)=\left[\begin{array}{c}\text{softmax}(s\left(k_1,q_n\right))\\ ⋮\\ \text{softmax}(s\left(k_N,q_n\right))\end{array}\right]=\left[\begin{array}{c}{\alpha }_{n1}\\ ⋮\\ {\alpha }_{nN}\end{array}\right]\in {\mathbb{R}}^N$$
  其中第j个分量为$({\alpha }_n{)}_j={\alpha }_{nj}$
• 为得到输出向量$h_n$，由于$V=[v_1,\dots ,v_N]\in {\mathbb{R}}^{D_v\times N}$，有
  $$h_n=V{\alpha }_n=\sum _{j=1}^N{v}_j({\alpha }_n{)}_j=\sum _{j=1}^N{\alpha }_{nj}{v}_j\in {\mathbb{R}}^{D_v\times 1}$$

自注意力基于矩阵形式的推导整理

考虑所有的查询向量$[q_1,\dots ,q_N]$，以统一得到$H=[h_1,\dots ,h_N]\in {\mathbb{R}}^{D_v\times N}$：

• 打分矩阵：
  $$S=\frac{1}{\sqrt{D_k}}{K}^{\top }Q\in {\mathbb{R}}^{N\times N}$$
  其中$S_{jn}=\frac{k_j^{\top }{q}_n}{\sqrt{D_k}}=s(k_j,q_n)=s_{jn}$。第 n 列 $S_{:,n}$ 是向量情形中的打分向量 $s^{(n)}$
• 权重矩阵：
  如前所述，对S按列做softmax，得到
  $$A=\mathrm{softmax}(S)\in {\mathbb{R}}^{N\times N}$$
  即对每一列 n，$A_{jn}=\frac{\exp (S_{jn})}{{\sum }_{\ell =1}^N\exp (S_{\ell n})}={\alpha }_{nj}.$ 因此，第 n 列 $A_{:,n}$ 就是向量情形中的权重向量 ${\alpha }_n$。
• 输出矩阵：
  基于值矩阵V和权重矩阵A，可以得到：
  $$H=VA\in {\mathbb{R}}^{D_v\times N}$$
  第 n 列满足 $H_{:,n}=V{A}_{:,n}=V{\alpha }_n=h_n$。展开为
  $$H_{:,n}=\sum _{j=1}^N{v}_j{A}_{jn}=\sum _{j=1}^N{\alpha }_{nj}{v}_j.$$
• 综合以上三步，自注意力的矩阵形式即为
  $$H=V\mathrm{softmax}\left(\frac{K^{\top }Q}{\sqrt{D_k}}\right)\in {\mathbb{R}}^{D_v\times N},$$