Java- 数组排序算法(冒泡,选择,插入,希尔排序,快速排序,并归排序,基数排序,堆排序)

本文详细介绍了排序算法，包括冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序、基数排序和堆排序。每种排序算法都有清晰的原理解释和代码实现，如冒泡排序的两层循环优化、快速排序的分治思想以及堆排序的堆调整过程。这些排序算法在时间和空间复杂度上有不同特点，适用于不同的场景需求。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

数组排序

文章目录

1, 冒泡排序

两个相邻的数比较，第一个数小向左/右换位置
冒泡的代码比较简单，两层循环，外层冒泡轮数，里层依次比较
我们看到嵌套循环，应该立马就可以得出这个算法的时间复杂度为O(n^2)
思考：如何优化？

    public static void main(String[] args) {
        int[] a = {1,3,2,5,4,7};
        System.out.println(Arrays.toString(sort(a)));
    }
    /*/
        冒泡排序
        1,比较数组，相邻的数，第一个比第二个大，交换位置
        2,没比一轮，得到一个最大的数或最小的数
        3,下一轮可以少一次循环
        4，依次循环，直到结束
     */
    public static int[] sort(int[] arr){
        int a = 0;
        //外层循环，判断循环多少次
        for (int i = 0; i < arr.length-1; i++) {
            //通过flag表示来减少没有意义的比较
            boolean flag = false;
            //内层循环，比较判断两个数，如果第一个数比第二个大，交换位置
            for (int j = 0; j < arr.length-i-1; j++) {
                /*
                    循环每次减1，不需要比最后一位数：arr.length-i-1  5 4 3 2 1
                    再依次比相邻两个数
                 */
                if (arr[j+1]>arr[j]) {
                    a = arr[j+1] ;
                    arr[j+1] = arr[j];
                    arr[j] = a;
                    flag = true;
                }
            }
            //如果没有交换位置，代表已经排序完成，可以终止循环了
            if (flag == false) {
                break;
            }
        }
        return arr;
    }

2, 选择排序

原理: 从低0个元素, 依次向后比较, 小的元素放前面

		int a = 0;//用来调换元素位置
        for (int i = 0; i < arr.length; i++) {
            //前面的数已经最小了,所以不用比较前面的了 j = 1+i
            for (int j = 1+i; j < arr.length; j++) {
                if (arr[i]>arr[j]){
                    a = arr[i];
                    arr[i] = arr[j];
                    arr[j] = a;
                }
            }
        }
        return arr;

3, 插入排序

从下标为1的元素开始, 把后面的元素插入到前面的元素中比较
后面的元素比前面的小, 就交换位置

    private static int[] InsertSort1(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            //方式一:
//            int j = i;
//            while (j>0 && arr[j] < arr[j-1]){
//                int a = arr[j];
//                arr[j] = arr[j-1];
//                arr[j-1] = a;
//                j--;
//            }
            //方式二
            for (int j = i; j >0 ; j--) {
                if (arr[j]<arr[j-1]){
                    int a = arr[j];
                    arr[j] = arr[j-1];
                    arr[j-1] = a;
                }
            }
        }
        return arr;
    }
}

4,希尔排序

定义一个增量ht分组, 每个子文件按照直接插入排序来排序, 下次一个排序按 ht/2 一半来继续排序, 直到ht=1

int[] a ={1,3,6,2,9,10,33,12}
如果ht = 4
1 -- 9  3 -- 10  6 -- 33 2 -- 12  比较 交换位置, 再按一半来比较

    private static int[] ShellSort(int[] arr) {
        //每次选数组长度的一半
        for (int h = arr.length/2; h >0 ; h/=2) {
            for (int i = h; i < arr.length; i++) {
                for (int j = i; j >h-1 ; j-=h) {
                    if (arr[j]<arr[j-1]){
                        int a = arr[j];
                        arr[j] = arr[j-1];
                        arr[j-1] = a;
                    }
                }
            }
        }
        return arr;
    }

每次选数组长度的一半效果不是很好
克鲁特序列: int h =1 ; h = 3*h +1

    //4 希尔排序 克努特序列 `int h =1 ; h = 3*h +1`
    private static int[] ShellSort(int[] arr) {
        //选取h
        int ht = 1;
        while (ht <= arr.length/3){
            ht = arr.length*3+1;
        }
        for (int h = ht; h >0 ; h=(h-1)/3) {
            for (int i = h; i < arr.length; i++) {
                for (int j = i; j >h-1 ; j-=h) {
                    if (arr[j]<arr[j-1]){
                        int a = arr[j];
                        arr[j] = arr[j-1];
                        arr[j-1] = a;
                    }
                }
            }
        }
        return arr;
    }

5, 快速排序

分治法: 比大小, 再分区

从数组中取出一个数作为基准数
分区:将比这个数大或等于的数放到他的右边, 小于他的数放到左边
再对左右区间重复第二步, 直到个区间只有一个数

实现思路: 挖坑填数

将基准数取出形成第一个坑
从后往前找比他小的数, 找到后挖出此数填到前一个坑中
从前向后找比他大或等于的数, 找到后也挖出填到前一个坑中
重复2, 3 步骤

package com.ccc.sort;

import java.util.Arrays;

public class Demo03Quick {
    public static void main(String[] args) {
        int[] arr = {66,111,666,24,41,5124,22,33,11,1,3,6,2,9,10,5,4,7};
        //调用排序方法 传入数组, 开始位置, 结束位置
        long start = System.nanoTime();
        quickSort(arr, 0, arr.length-1);
        long end = System.nanoTime();
        System.out.println(end-start);//5800
        System.out.println(Arrays.toString(arr));
    }
    public static  void  quickSort(int[] arr , int start, int end){
        //找出左右两区的索引位置, 然后对左右分区进行递归调用
        if (start<end){//直到开始和结束一致
            int index =getIndex(arr,start,end);
            //左半区 从0 - index-1
            quickSort(arr,start, index-1);
            //右半区 从end- index+1
            quickSort(arr,index+1, end);
        }

    }
    //1. 将基准数取出形成第一个坑
    //2. 从后往前找比他小的数, 找到后挖出此数填到前一个坑中
    //3. 从前向后找比他大或等于的数, 找到后也挖出填到前一个坑中
    private static int getIndex(int[] arr, int start, int end) {
        int i = start;
        int j = end;
        //1 ,挖出第一个坑位
        int first = arr[i];//第一个坑位
        while (i<j){

            //2. 从后往前找比他小的数, 找到后挖出此数填到前一个坑中
            while (i<j  && arr[j] >=first){
                j--;// j: end ,从后往前找
            }

            if (i<j){ //判断是否重合
                //上一个坑位是 arr[start]对应arr[i] , arr[j]是现在挖到坑的值填到上一个
                arr[i] = arr[j];
                i++;//前面一个坐标往右移
            }
            //3. 从前向后找比他大或等于的数, 找到后也挖出填到前一个坑中
            while (i<j && arr[i] <first){
                i++;// i: start ,从前往后找
            }
            if (i<j){//判断是否重合
                //上一个坑位是 arr[j] , arr[i]是现在挖到坑的值填到上一个
                arr[j] = arr[i];
                j--;//后面一个坐标往左移
            }
        }
        //最后把基数填到最后一个坑中
        arr[j] = first;
        return j;
    }


}

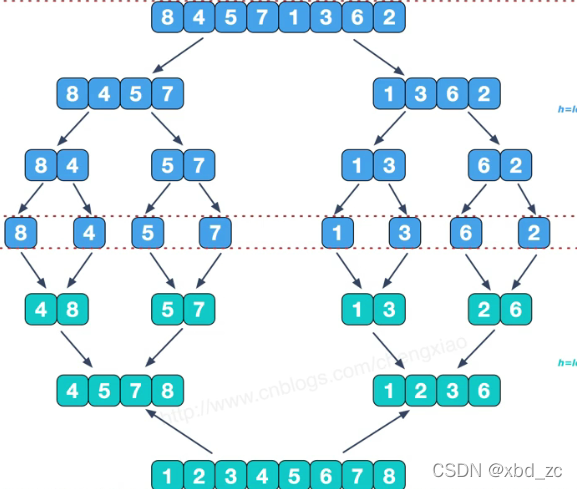
6, 归并排序

拆分
- 把元素拆分成N/2的元素
比较
- 比较拆分后元素谁小
归并
- 小的元素放临时数组

请添加图片描述

package com.ccc.sort;

import java.util.Arrays;

public abstract class Demo04MergeSort {
    public static void main(String[] args) {
        int[] arr = {66,111,666,24,41,5124,22,33,11,1,3,6,2,9,10,5,4,7};
//        int[] arr = {1,3,5,6,2,5,6,7};
        //调用排序方法 传入数组, 开始位置, 结束位置
        long start = System.nanoTime();
        mergeSort(arr, 0,arr.length-1);
        long end = System.nanoTime();
        System.out.println(Arrays.toString(arr));
    }

    private static void mergeSort(int[] arr, int start, int end) {
        //计算中间坐标
        int center = (start+end)/2;
        if (start<end){
            //拆分左边
            mergeSort(arr,start,center);
            //拆分右边
            mergeSort(arr,center+1,end);
            //归并操作
            merge(arr, start,center, end);
        }
    }
    //归并
    private static void merge(int[] arr, int start,int center, int end) {
        int[] temps = new int[(end-start)+1];
        //定义左边开启坐标
        int i = start;
        //右边的开始坐标
        int j = center+1;
        //临时数组的坐标
        int t = 0;
        //比较左右两个数组元素大小往临时数组中放
        //如果左边开始坐标和中间坐标不重合 (代表还有数) && 右边开始坐标和结束坐标不重合 (代表还有数)
        while (i<=center && j<=end){
            //两半的开始坐标数开始比较   如果右边边比左边的小 就把右边的放到临时数组里
            if (arr[i]>arr[j]){
                temps[t] = arr[j];
                j++;
                //如果左边比右边的小 就把左边的放到临时数组里
            }else{
                temps[t] = arr[i];
                i++;
            }
            t++;//临时数组坐标++
        }
        //处理剩余元素
        //如果左边还有剩余数
        while (i<=center){
            temps[t] = arr[i];
            i++;
            t++;
        }
        //如果有边还有剩余数
        while (j<=end){
            temps[t] = arr[j];
            j++;
            t++;
        }
        //将临时数组中的元素放到原数组中
        for (int k = 0; k < temps.length; k++) {
            arr[k+start] = temps[k];
        }
    }
}

7,基数排序

每个数组抽出来,在放出来
1, 准备10个桶 0~9
2, 根据数组元素个位数 0 放到 0桶中 ,1 放到 1桶中…直到放完
3, 放完之后,再拿出来, 从0桶的第一个放到最后一个, 再从1桶中第一个放到最后一个…直到取完
4, 再根据元素的十位,百位,千位…放到桶中,再取出

方式一:

二维数组:

package com.ccc.sort;

import java.util.Arrays;

public class Demo05Cardinality2 {

    public static void main(String[] args) {
        int[] arr = {66,111,666,24,41,5124,22,33,11,1,3,6,2,9,10,5,4,7};
        long start = System.nanoTime();
        cardinalitySort(arr);
        long end = System.nanoTime();
        System.out.println(Arrays.toString(arr));
        System.out.println(end-start);//42600
    }

    private static void cardinalitySort(int[] arr) {
        //定义二维数组,放10个桶
        int[][] tempArr = new int[10][arr.length];
        //定义统计数组
        int[] count = new int[10];
        int max = getMax(arr);
        //循环轮次
        for (int i = 0; i < max; i++) {
            int division = (int) Math.pow(10,i);
            for (int j = 0; j < arr.length; j++) {
                //取到个位十位...的值
                int num = arr[j]/division % 10;
                tempArr[num][count[num]++] =arr[j];
            }
            //取出桶中元素
            int index = 0;
            for (int k = 0; k < count.length; k++) {
                if (count[k]!=0){
                    for (int h = 0; h < count[k]; h++) {
                        //从桶中取出元素放回原数组
                        arr[index] = tempArr[k][h];
                        index++;
                    }
                    count[k] = 0;//清除上一次统计的个数
                }
            }
        }
    }

    //计算数组中最大值有几位
    private static int getMax(int[] arr) {
        int max = 0;
        for (int i = 0; i < arr.length; i++) {
            if (arr[i]>max){
                max = arr[i];
            }
        }
        return String.valueOf(max).length();

    }
}

方式二:

package com.ccc.sort;

import java.util.Arrays;

public class Demo05Cardinality {

    public static void main(String[] args) {
        int[] arr = {66,111,666,24,41,5124,22,33,11,1,3,6,2,9,10,5,4,7};
        long start = System.nanoTime();
        int[] result = cardinalitySort(arr);
        long end = System.nanoTime();
        System.out.println(Arrays.toString(result));
        System.out.println(end-start);//104800
    }

    private static int[] cardinalitySort(int[] arr) {
        int []result = new int[arr.length];
        int [] count = new int[10];
        int max = getMax(arr);

        for (int i = 0; i < max; i++) {
            int division = (int) Math.pow(10,i);
            for (int j = 0; j < arr.length; j++) {
                //取到个位十位...的值
                int num = arr[j]/division % 10;
                count[num]++;
            }
            for (int m = 1; m < count.length; m++) {
                count[m] = count[m] +count[m-1];
            }

            for (int n = arr.length-1; n >=0 ; n--) {
                int num = arr[n]/division %10;
                result[--count[num]] = arr[n];
            }
            System.arraycopy(result,0,arr,0,arr.length);
            Arrays.fill(count,0);
        }
        return result;
    }
    //计算数组中最大值有几位
    private static int getMax(int[] arr) {
        int max = 0;
        for (int i = 0; i < arr.length; i++) {
            if (arr[i]>max){
                max = arr[i];
            }
        }
        return String.valueOf(max).length();

    }
}

8,堆排序

1 将带排序序列构成一个大顶堆(顶部最大)
2 将顶部元素与末尾元素交换, 末尾最大
3 在将除了最后一个元素前面的元素形成大顶堆 , 在和末尾交换, 如此重复即可

package com.ccc.sort;

import java.util.Arrays;

public class Demo06Heapsort {
    public static void main(String[] args) {
        int[] arr = {66,111,666,24,41,5124,22,33,11,1,3,6,2,9,10,5,4,7};
        long start = System.nanoTime();
        heapSort(arr);
        long end = System.nanoTime();
        System.out.println(Arrays.toString(arr));
        System.out.println(end-start);//8900
    }

    private static void heapSort(int[] arr) {
        //调整成大顶堆的方法
        //定义开始调整的位置
        int start = (arr.length-1)/2;
        //循环调整
        for (int i = start; i >=0 ; i--) {
            toMaxHeap(arr,arr.length,i);
        }
        //经过上面的操作,已经把数组变成了大顶堆, 把根元素和最后一个元素调换
        for (int i = arr.length-1 ; i > 0 ; i--){
            //调换
            int t = arr[0];
            arr[0] = arr[i];
            arr[i]  = t;
            //换完之后把剩余元素调成大顶堆
            toMaxHeap(arr,i,0);
        }
    }

    /**
     *
     * @param arr       排序的数组
     * @param size    调整的元素个数
     * @param index     从哪里开始调整
     */
    private static void toMaxHeap(int[] arr, int size, int index) {
        //获取左右子节点的索引
        int left = index*2+1;
        int right = index*2+2;
        //查找最大节点所对应的索引
        int max = index;
        if (left < size && arr[left] > arr[max]){
            max = left;
        }
        if (right < size && arr[right] > arr[max]){
            max = right;
        }
        //找到最大值是调换位置
        if (max!=index){
            int t = arr[max];
            arr[max] = arr[index];
            arr[index] = t;
            //调换完之后, 可能影响下面的子树不是大顶堆, 再次调换
            toMaxHeap(arr,size,max);
        }
    }
}