树结构
树的优点
我们学习了多种数据结构来保存数据,为什么要用树结构来保存数据呢?
树结构和数组/链表/哈希表的对比有什么优点呢?
- 数组
-
优点:能根据下标值访问效率高,若根据元素查找要先对数组排序,在进行二分查找;
-
缺点: 需要对数组排序,生成有序数组;在数值插入和删除操作时,需要大量的位移操作,效率较低;
- 链表
-
优点: 插入和删除操作效率很高;
-
缺点:查找效率较低,需要从头依次访问数据项;
3.哈希表
- 优点:插入/查询/删除效率都很高;
- 缺点:空间利用率不高,由于底层实现是数组,有些单元未被利用;元素无序,不能固定顺序遍历;不能快速查找最大值或最小值等特殊值。
这里树结构综合了以上数据结构的一些优点,但是也不一定最好(比如查找效率方面不如哈希表)
树的术语
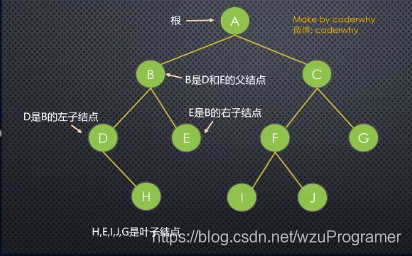
-
树(Tree):n(n >= 0)个节点构成的有限集合;
-
对于一颗非空树:有一个"根(Root)"节点r,其余节点可分为m个互不相交的有限集T1,T2,T3…Tm,每个集合本身又是树,称为子树(SubTree);
-
节点的度(Degree):节点的子树个数(二叉树只有0,1,2三个值);
-
树的度:树的所有节点中最大的度数;
-
叶(子)节点:度为0的节点;
-
父节点:有子树的节点;
-
子节点:A为B的父节点,那么B为A的子节点;
-
兄弟节点:有同一父节点的各节点;
-
路径及路径长度:从一个节点到另一个节点,经过的边为路径的长度;
-
节点的层次: 根节点在第一层,其他节点都是其父节点的层次+1;
-
树的深度:树中所有节点的最大层次是输的深度.
树的表示方式
- 普通表示法
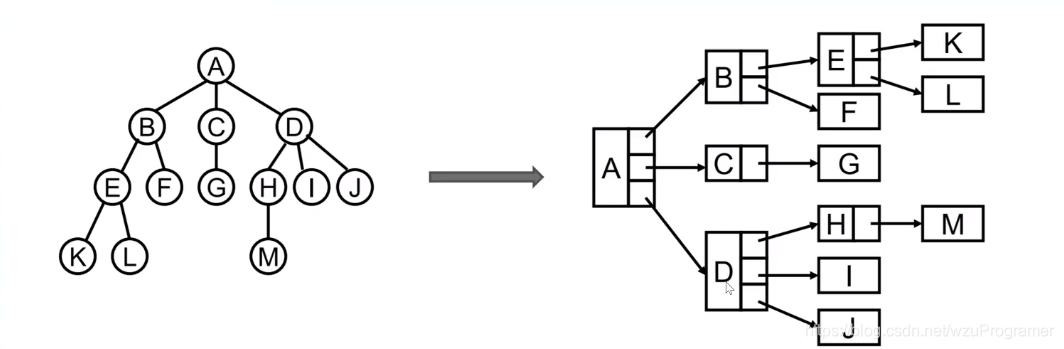
- 兄弟表示法
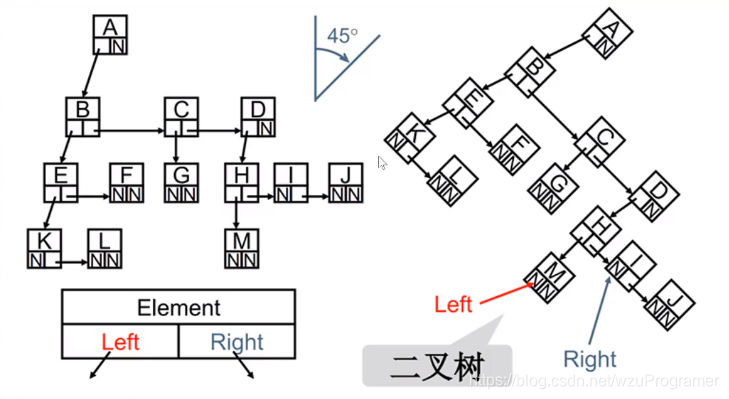
所有树本质上都可以用二叉树表示
二叉树
- 二叉树
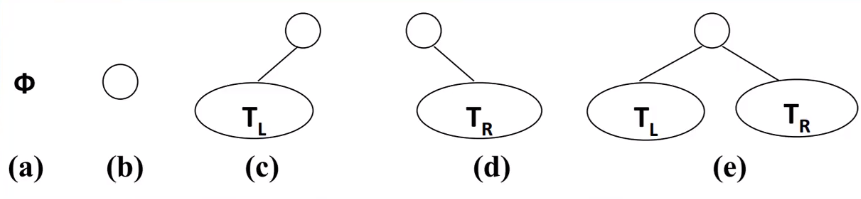
二叉树:每个节点最多只有两个子节点的树。
二叉树可以为空,也可以是由根节点和称为其左子树TL和右子树TR的两个二叉树组成。
- 二叉树的特性
- 二叉树第i层的最大节点树:2^(i - 1);
- 深度为k的二叉树的最大节点总数为2^k - 1;
- 对任意非空二叉树,叶节点的个数(no) = 度为2的非叶节点个数(n2) + 1;
- 完美二叉树和完全二叉树(Complete Binary Tree)
完美二叉树:除叶节点其余节点的度都为2;
完全二叉树:
- 除最后一层 其他各层的节点数达到最大;
- 最后一层从左到右叶节点连续存在;
- 完美二叉树是特殊的完全二叉树;
- 二叉树的存储
二叉树的存储常见有数组和链表;
- 数组方法在存储非完全二叉树时会造成空间浪费;
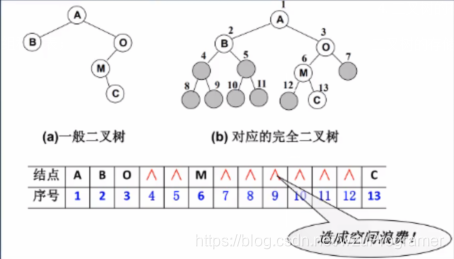
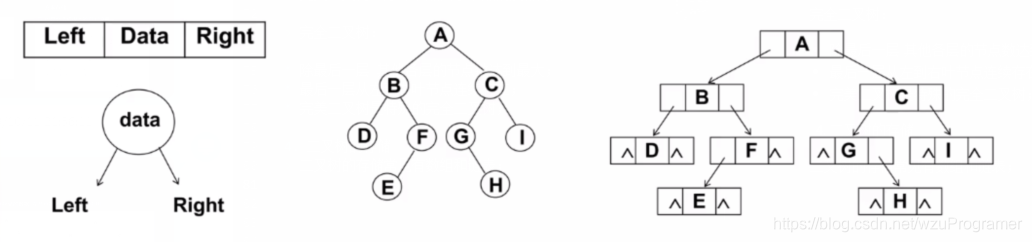
- 链表将每个节点封装成Node,Node包含data,左节点的引用,右节点的引用。
二叉搜索树
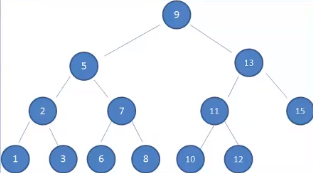
查找的最大次数就是树的深度,这里运用了二分查找的思想。
根据这个思路封装一个二叉搜索树,每个节点两个指向。左指向key比该节点key小的节点,右指向key比该节点key大的节点。
//封装二叉搜索树
function BinarySearchTree() {
//属性
this.root = null;
//内部节点类
function Node(key) {
this.key = key;
this.left = null;
this.right = null;
}
//方法
//1.插入一个新键
BinarySearchTree.prototype.insert = function(key) {
//1.创建节点
var newNode = new Node(key);
//2.判断根节点是否有值
if(this.root == null) {
this.root = newNode;
}else {
this.insertNode(this.root,newNode);
}
}
BinarySearchTree.prototype.insertNode = function(node,newNode) {
//向左查找
if(node.key > newNode.key) {
if(node.left == null) {
node.left = newNode;
}else {
this.insertNode(node.left,newNode);
}
}else { //向右查找
if(node.right == null) {
node.right = newNode;
}else {
this.insertNode(node.right,newNode);
}
}
}
// 遍历
// 1.先序遍历
BinarySearchTree.prototype.preOrderTraversal = function (handler) {
this.preOrderTraversalNode(this.root,handler);
}
BinarySearchTree.prototype.preOrderTraversalNode = function(node,handler) {
if(node != null) {
handler(node.key);
this.preOrderTraversalNode(node.left,handler);
this.preOrderTraversalNode(node.right,handler);
}
}
// 2.中序遍历
BinarySearchTree.prototype.inOrderTraversal = function (handler) {
this.inOrderTraversalNode(this.root,handler);
}
BinarySearchTree.prototype.inOrderTraversalNode = function(node,handler) {
if(node != null) {
this.inOrderTraversalNode(node.left,handler);
handler(node.key);
this.inOrderTraversalNode(node.right,handler);
}
}
// 3.后序遍历
BinarySearchTree.prototype.postOrderTraversal = function (handler) {
this.postOrderTraversalNode(this.root,handler);
}
BinarySearchTree.prototype.postOrderTraversalNode = function(node,handler) {
if(node != null) {
this.postOrderTraversalNode(node.left,handler);
this.postOrderTraversalNode(node.right,handler);
handler(node.key);
}
}
//4.最大值和最小值
BinarySearchTree.prototype.min = function() {
var node = this.root;
while(node.left) {
node = node.left;
}
return node.key;
}
BinarySearchTree.prototype.max = function() {
var node = this.root;
while(node.right) {
node = node.right;
}
return node.key;
}
//5.查找节点(循环方法)
BinarySearchTree.prototype.search = function(key) {
var node = this.root;
if(node == null) {
return false;
}else {
while(node != null) {
if(key < node.key) {
node = node.left;
}else if(key > node.key) {
node= node.right;
}else {
return true;
}
}
}
return false;
}
//6. 删除节点
BinarySearchTree.prototype.remove =function(key) {
//1. 寻找要删除的节点
//1.1 定义变量,保存一些信息
current = this.root;
parent = null;
isLeftChild = true;
//1.2 开始寻找要删除的节点
while(current.key != key) {
parent = current;
if(key < current.key) {
current = current.left;
isLeftChild =true;
} else {
current = current.right;
isLeftChild = false;
}
//一种情况,没有找到要删除的节点
if(current == null) {
return false;
}
}
//2 找到节点,开始根据情况删除节点(current.key == key)
//2.1 删除节点是叶子节点时
if(current.left == null && current.right == null) {
if(current == this.root) { //2.1.1节点正好是根节点
this.root = null;
}else if(isLeftChild) { //2.1.2节点是左子节点
parent.left = null;
}else {
parent.right = null;
}
}
//2.2 删除有一个子节点的节点
else if(current.right == null) { //2.2.1子节点是左子节点
if(current == this.root) {
this.root = current.left;
}else if(isLeftChild) {
parent.left = current.left;
}else {
parent.right = current.left;
}
}else if(current.left == null) { //2.2.2子节点是右子节点
if(current == this.root) {
this.root = current.right;
}else if(isLeftChild) {
parent.left = current.right;
}else {
parent.right = current.right;
}
}
//2.3 删除有两个子节点的节点(这里非常复杂,我们用寻找后继点来覆盖删除节点)
else {
//2.3.1找到后继点
var successor = this.getSuccessor(current);
//2.3.2判断是根节点
if(current == this.root) {
this.root =successor;
}else if(isLeftChild) {
parent.left = successor;
}else {
parent.right = successor;
}
//2.3.3让后继的左子树 = 原删除节点的左子树
successor.left = current.left;
//最后我们还有一种情况没有考虑到,就是删除节点的右子树不是一个节点时,将后继提上来,他的右指向就是后继的原父节点
//在封装寻找后继点函数时我们将它考虑进去;
}
return true;
}
BinarySearchTree.prototype.getSuccessor = function(delNode) {
//定义变量
var successorParent = delNode;
var successor = delNode;
var current = delNode.right;
//找到后继点
while(current != null) {
successorParent = successor;
successor = current;
current = current.left;
}
//前面所说后继节点不是删除节点的右节点的情况
if(successor != delNode.right) {
successorParent.left = successor.right;
successor.right = delNode.right;
}
return successor;
}
}
//测试
var binarySearchTree = new BinarySearchTree();
binarySearchTree.insert(20);
binarySearchTree.insert(11);
binarySearchTree.insert(30);
binarySearchTree.insert(25);
binarySearchTree.insert(40);
binarySearchTree.insert(35);
binarySearchTree.insert(50);
binarySearchTree.insert(36);
binarySearchTree.remove(30);
var resultString = "";
binarySearchTree.preOrderTraversal(function(key) {
resultString += key + " ";
});
console.log(resultString);
在删除节点操作中,2.3步比较麻烦,总结有一下规律:
删除的节点有两个子节点,甚至子节点还有子节点,所以我们要从下面的子节点来代替删除的节点,这个节点有什么规律?
-
比current节点要大一点点或者小一点点;
-
这两个点就是current左子树的最大值(前驱)或者右子树的最小值(后继);
-
这里我们以后继为例。




















 174
174

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








