《基于张量网络的学习入门》学习笔记2
量子逻辑门
量子信息处理的本质就是对编码的量子态进行一系列的幺正演化,对qubit最基本的幺正操作被称为逻辑门。在量子计算机的运算中,经常用量子位和量子逻辑门的量子电路来描述。
单量子逻辑门
恒等操作
I = ( 1 0 0 1 ) = ∣ 0 > < 0 ∣ + ∣ 1 > < 1 ∣ \displaystyle I = \left( \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right) = \left| 0 \right> \left< 0 \right| + \left| 1 \right> \left< 1 \right| I=(1001)=∣0⟩⟨0∣+∣1⟩⟨1∣
这里的 ∣ 0 ⟩ ⟨ 0 ∣ \mathinner{|0\rangle}\mathinner{\langle0|} ∣0⟩⟨0∣是左右矢的外积
泡利-X门(Pauli-X gate)
泡利-X门操作单个量子比特,相当于经典的逻辑非门。如操作前量子位为 ∣ 1 ⟩ \mathinner{|1\rangle} ∣1⟩,经过泡利-X门后会转换为 ∣ 0 ⟩ \mathinner{|0\rangle} ∣0⟩.
其矩阵表示为:

泡利-Y门(Pauli-Y gate)
泡利-Y门操作单个量子比特,类似于复数操作
其矩阵表示为:
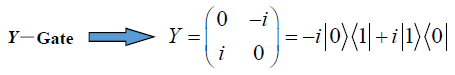





 本文介绍了量子逻辑门的基础知识,包括单量子逻辑门如Pauli-X、Y、Z门,阿达马门,以及双量子逻辑门CNOT和受控互换门SWAP。此外,还探讨了三量子逻辑门的Toffoli门和量子门在并行计算中的重要性,阐述了量子信息处理如何通过张量网络助力机器学习。
本文介绍了量子逻辑门的基础知识,包括单量子逻辑门如Pauli-X、Y、Z门,阿达马门,以及双量子逻辑门CNOT和受控互换门SWAP。此外,还探讨了三量子逻辑门的Toffoli门和量子门在并行计算中的重要性,阐述了量子信息处理如何通过张量网络助力机器学习。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 520
520

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








