Vector Autoregressive Methods
在此之前,我们已经介绍了预测单一/单变量时间序列的经典方法,如 ARIMA(自回归整合移动平均)模型和简单线性回归模型。 我们了解到,使用自回归整合移动平均模型时,静止性是一个必要条件,而使用线性回归模型时则无需强加这一条件。 在本笔记本中,我们将预测问题扩展到一个更广义的框架中,即处理具有多个时间变量的多变量时间序列。 更具体地说,我们将介绍向量自回归(VAR)模型,并展示如何将其用于预测多变量时间序列。
Multivariate Time Series Model
如前几章所示,使用简单的单变量方法(如 ARIMA)的主要优势之一是能够仅使用一个变量的过去值来预测该变量的未来值。 然而,我们知道,我们观察到的大多数(如果不是全部)变量实际上都依赖于其他变量。 大多数情况下,我们收集的信息受限于我们测量相关变量的能力。 例如,如果我们想研究某个城市的天气,我们可以测量一段时间内的温度、湿度和降水量。 但是,如果我们只有一个温度计,那么我们就只能收集温度的数据,这实际上将我们的数据集缩小为单变量时间序列。
现在,如果我们有多个时间序列(不止一个变量的纵向测量),我们实际上可以使用多元时间序列模型来了解不同变量随时间变化的关系。 通过利用相关序列提供的额外信息,这些模型通常能比单变量时间序列模型提供更好的预测。
在本节中,我们将介绍理解矢量自回归模型(一类多变量时间序列模型)所需的基础信息,使用的框架类似于前几章中的单变量时间序列,并将其扩展到多变量情况。
Definition: Univariate vs Multivariate Time Series
时间序列可以是单变量时间序列,也可以是多变量时间序列。 单变量时间序列由在相等时间增量内连续记录的单个观测值组成。 在处理单变量时间序列模型(如 ARIMA)时,我们通常指的是包含自变量滞后值的模型。
另一方面,多元时间序列有不止一个时间变量。 对于一个多变量过程,在一段时间内会同时观测到几个相关的时间序列。 作为单变量情况的延伸,多变量时间序列模型涉及两个或多个输入变量,并利用不同时间序列变量之间的相互关系。
import numpy as np
import pandas as pd
import statsmodels.tsa as tsa
from statsmodels.tsa.vector_ar.var_model import VAR, FEVD
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.tsa.stattools import acf, adfuller, ccf, ccovf, kpss
from statsmodels.graphics.tsaplots import plot_acf
import matplotlib.pyplot as plt
import mvts_utils as utils
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
pd.set_option('display.max_rows', None)
pd.set_option('display.max_columns', None)
%load_ext autoreload
%autoreload 2
Example 1: Multivariate Time Series
A. Air Quality Data from UCI
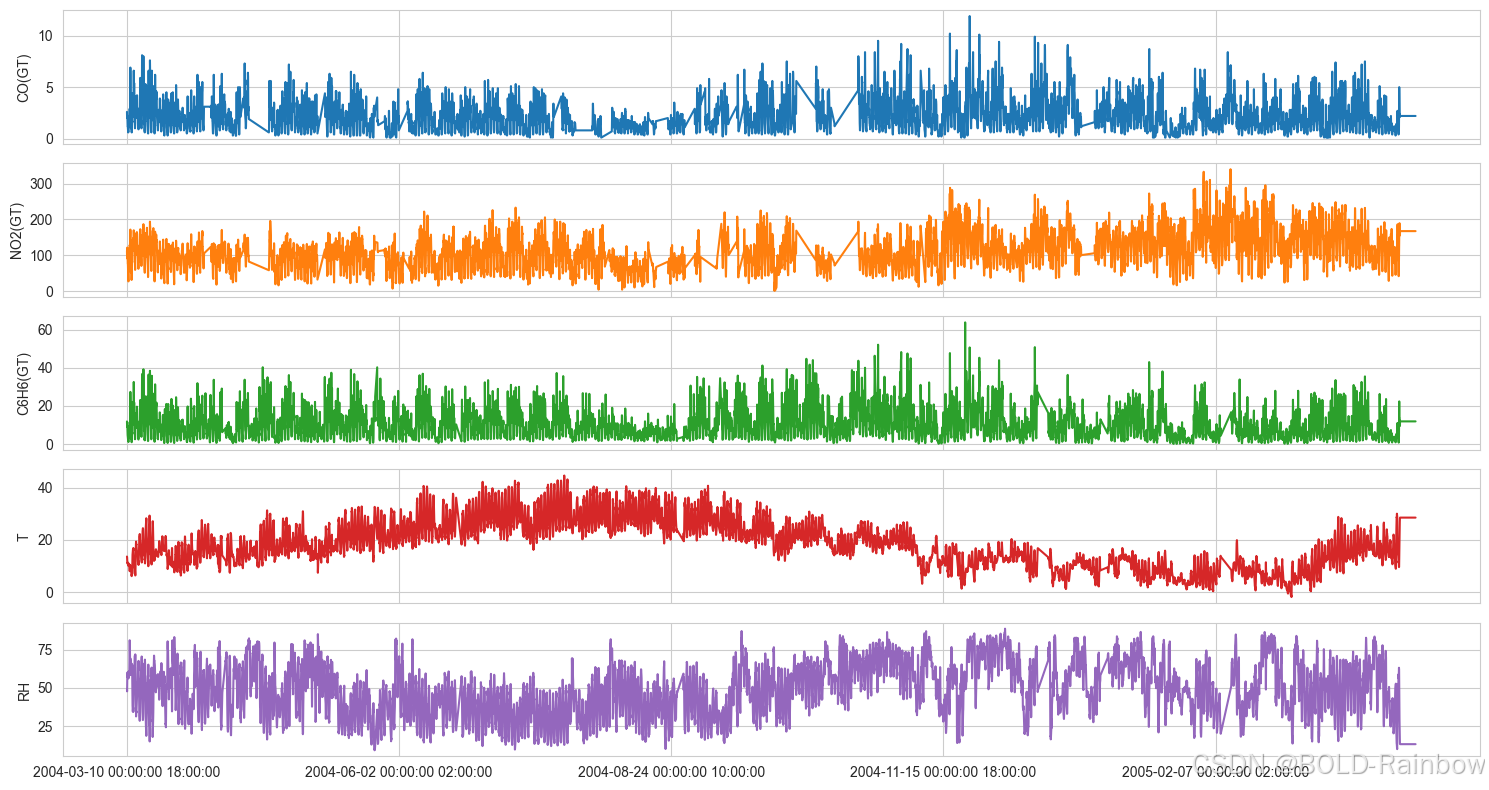
数据集包含一个空气质量化学多传感器装置的每小时平均测量值,该装置位于意大利某城市的污染区。 数据集可在此处下载。
aq_df = pd.read_excel("../data/AirQualityUCI/AirQualityUCI.xlsx", parse_dates=[['Date', 'Time']])\
.set_index('Date_Time').replace(-200, np.nan).interpolate()
aq_df.head(2)
fig,ax = plt.subplots(5, figsize=(15,8), sharex=True)
plot_cols = ['CO(GT)', 'NO2(GT)', 'C6H6(GT)', 'T', 'RH']
aq_df[plot_cols].plot(subplots=True, legend=False, ax=ax)
for a in range(len(ax)):
ax[a].set_ylabel(plot_cols[a])
ax[-1].set_xlabel('')
plt.tight_layout()
plt.show()
B. Global Health from The world Bank
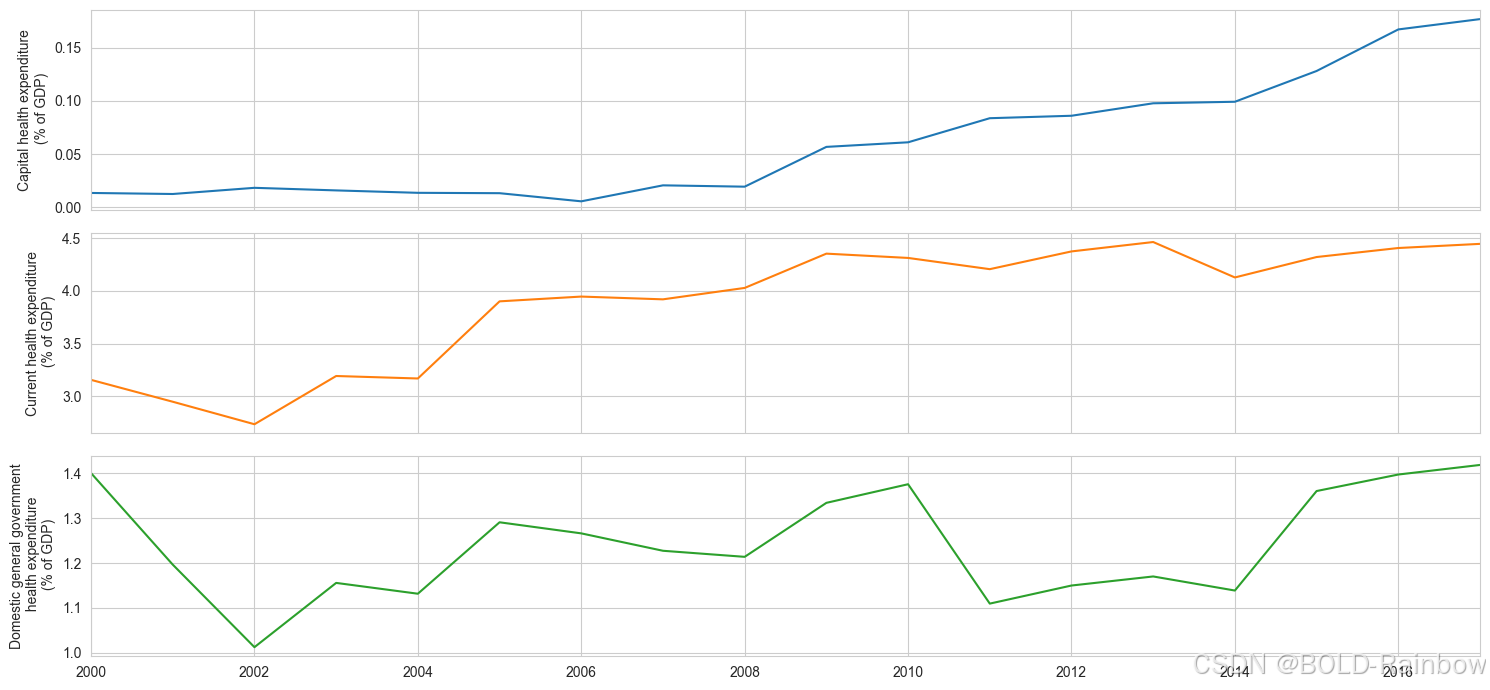
该数据集综合了各种来源的主要卫生统计数据,提供了全球卫生和人口趋势概览。 它包括 200 多个国家的营养、生殖健康、教育、免疫接种和疾病方面的信息。 该数据集可在此处下载。
ind_df = pd.read_csv('../data/WorldBankHealth/WorldBankHealthPopulation_SeriesSummary.csv')\
.loc[:,['series_code', 'indicator_name']].drop_duplicates().reindex()\
.sort_values('indicator_name').set_index('series_code')
hn_df = pd.read_csv('../data/WorldBankHealth/WorldBankHealthPopulation_HealthNutritionPopulation.csv')\
.pivot(index='year', columns='indicator_code', values='value')
cols = ['SH.XPD.KHEX.GD.ZS', 'SH.XPD.CHEX.GD.ZS', 'SH.XPD.GHED.GD.ZS']
health_expenditure_df = hn_df.loc[np.arange(2000, 2018), cols]\
.rename(columns = dict(ind_df.loc[cols].indicator_name\
.apply(lambda x: '_'.join(x.split('(')[0].split(' ')[:-1]))))
health_expenditure_df.index = pd.date_range('2000-1-1', periods=len(health_expenditure_df), freq="A-DEC")
health_expenditure_df.head(3)
fig, ax = plt.subplots(3, 1, sharex=True, figsize=(15,7))
health_expenditure_df.plot(subplots=True, ax=ax, legend=False)
y_label = ['Capital health expenditure', 'Current health expenditure',
'Domestic general government\n health expenditure']
for a in range(len(ax)):
ax[a].set_ylabel(f"{y_label[a]}\n (% of GDP)")
plt.tight_layout()
plt.show()
C. US Treasury Rates
1982 年 1 月至 2016 年 12 月(每周) https://essentialoftimeseries.com/data/ 此示例数据集包含 1982 年 1 月至 2016 年 12 月期间美国国库券利率的每周数据。数据集可在此处下载。
treas_df = pd.read_excel("../data/USTreasuryRates/us-treasury-rates-weekly.xlsx")
treas_df = treas_df.rename(columns={'Unnamed: 0': 'Date'}).set_index('Date')
treas_df.index = pd.to_datetime(treas_df.index)
treas_df.head(3)
treas_df = pd.read_excel("../data/USTreasuryRates/us-treasury-rates-weekly.xlsx")
treas_df = treas_df.rename(columns={'Unnamed: 0': 'Date'}).set_index('Date')
treas_df.index = pd.to_datetime(treas_df.index)
treas_df.head(3)

D. Jena Climate Data
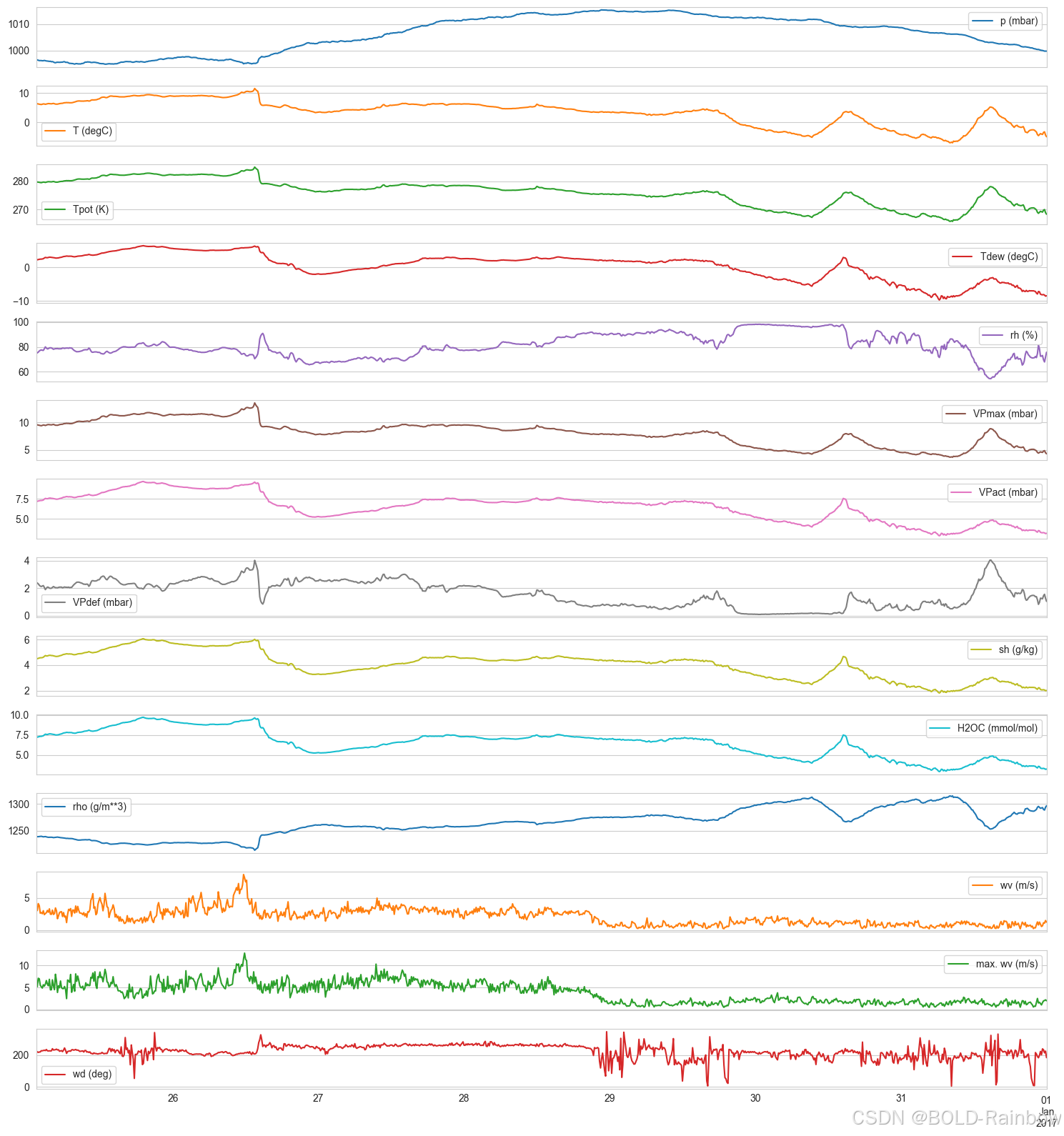
德国耶拿马克斯-普朗克生物地球化学研究所气象站 2009 年至 2016 年记录的时间序列数据集。 它包含每 10 分钟记录一次的 14 种不同数量(如气温、气压、湿度、风向等)。 您可以在这里下载数据。
jena_data = pd.read_csv('../data/jena_climate_2009_2016.csv')
jena_data['Date Time'] = pd.to_datetime(jena_data['Date Time'])
jena_data = jena_data.set_index('Date Time')
jena_data.head(3)
fig,ax = plt.subplots(jena_data.shape[-1], figsize=(15,16), sharex=True)
jena_data.iloc[-1000:].plot(subplots=True, ax=ax)
ax[-1].set_xlabel('')
plt.tight_layout()
plt.show()
Foundations
在我们讨论 VAR 之前,我们在下面概述了一些基本概念,我们需要了解这些概念。
Weak Stationarity of Multivariate Time Series
与单变量情况一样,在应用 VAR 模型之前,我们需要满足的条件之一是平稳性,特别是弱平稳性。 无论是在单变量还是多变量情况下,时间序列的前两个矩都是时间不变的。 下面我们将更正式地描述弱静止性。
考虑N-维度的时间序列 y t = [ y 1 , t , y 2 , t , … , y N , t ] ′ \mathbf{y}_t=[y_{1,t},y_{2,t},\ldots,y_{N,t}]^{\prime} yt=[y1,t,y2,t,…,yN,t]′,如果前两个矩是有限的,并且在时间上恒定不变,即可以说这是弱平稳的,
- E [ y t ] = μ E[y_t]=\mu E[yt]=μ
- E [ ( y t − μ ) ( y t − μ ) ′ ] ≡ Γ 0 < ∞ E\left[(\mathbf{y}_t-\boldsymbol{\mu})(\mathbf{y}_t-\boldsymbol{\mu})^{\prime}\right]\equiv\boldsymbol{\Gamma}_0<\infty E[(yt−μ)(yt−μ)′]≡Γ0<∞ for all t
- E [ ( y t − μ ) ( y t − h − μ ) ′ ] ≡ Γ h E\left[(\mathbf{y}_t-\boldsymbol{\mu})(\mathbf{y}_{t-h}-\boldsymbol{\mu})^{\prime}\right]\equiv\boldsymbol{\Gamma}_h E[(yt−μ)(yt−h−μ)′]≡Γh for all t t t and h h h
其中,期望是逐个元素接受 y t y_t yt的联合分布:
- μ \mu μ是向量 μ = [ μ 1 , μ 2 , ⋯ , μ N ] \mu=[\mu_1,\mu_2,\cdots,\mu_N] μ=[μ1,μ2,⋯,μN]的均值
- Γ 0 \Gamma_0 Γ0是 N × N N\times N N×N维度的协变量矩阵其中第 i i i个对角线元素是 y i , t y_{i,t} yi,t的方差,而且 ( i , j ) (i,j) (i,j)个元素是 y i , t y_{i,t} yi,t和 y j , t y_{j,t} yj,t之间的协方差
- Γ h \Gamma_h Γh是滞后 h h h的交叉协方差矩阵
Obtaining Cross-Correlation Matrix from Cross-Covariance Matrix
在处理多元时间序列时,我们可以使用交叉协方差函数(CCVF)和交叉相关函数(CCF)来研究一个变量对另一个变量的可预测性。 为此,我们首先要定义两个变量之间的交叉协方差,然后估计一个变量与另一个时移变量之间的交叉相关性。 这将告诉我们一个时间序列是否可能与另一个时间序列的过去滞后相关。 换句话说,CCF 用于识别一个变量的滞后期,这些滞后期可能是另一个变量的有用预测指标。
在滞后为0时:
让
Γ
0
\Gamma_0
Γ0表示滞后为0时的协方差矩阵,
D
D
D表示
N
×
N
N\times N
N×N维对角线矩阵包含了
y
i
,
t
,
t
=
1
,
⋯
,
N
y_{i,t}, t=1,\cdots,N
yi,t,t=1,⋯,N的标准偏差。
y
t
y_t
yt的相关矩阵被定义为:
ρ
0
=
D
−
1
Γ
0
D
−
1
\rho_0=\mathbf{D}^{-1}\Gamma_0\mathbf{D}^{-1}
ρ0=D−1Γ0D−1
其中
ρ
0
\rho_0
ρ0的第
(
i
,
j
)
(i,j)
(i,j)个元素是
t
t
t时刻
y
i
,
t
y_{i,t}
yi,t和
y
j
,
t
y_{j,t}
yj,t的相关系数:
ρ
i
,
j
(
0
)
=
C
o
v
[
y
i
,
t
,
y
j
,
t
]
σ
i
,
t
σ
j
,
t
\rho_{i,j}(0)=\frac{Cov\left[y_{i,t},y_{j,t}\right]}{\sigma_{i,t}\sigma_{j,t}}
ρi,j(0)=σi,tσj,tCov[yi,t,yj,t]
在滞后为
h
h
h时
让
Γ
h
=
E
[
(
y
t
−
μ
)
(
y
t
−
h
−
μ
)
′
]
\mathbf{\Gamma}_h=E\left[(\mathbf{y}_t-\boldsymbol{\mu})(\mathbf{y}_{t-h}-\boldsymbol{\mu})^{\prime}\right]
Γh=E[(yt−μ)(yt−h−μ)′]表示
y
t
y_t
yt滞后-h的 的协方差交叉方差矩阵,滞后-h的交叉相关矩阵定义为:
ρ
h
=
D
−
1
Γ
h
D
−
1
\rho_h=\mathbf{D}^{-1}\Gamma_h\mathbf{D}^{-1}
ρh=D−1ΓhD−1
ρ
h
\rho_h
ρh的第
(
i
,
j
)
(i,j)
(i,j)个元素是
y
i
,
t
y_{i,t}
yi,t和
y
j
,
t
−
h
y_{j,t-h}
yj,t−h的相关系数:
ρ
i
,
j
(
h
)
=
C
o
v
[
y
i
,
t
,
y
j
,
t
−
h
]
σ
i
,
t
σ
j
,
t
\rho_{i,j}(h)=\frac{Cov\left[y_{i,t},y_{j,t-h}\right]}{\sigma_{i,t}\sigma_{j,t}}
ρi,j(h)=σi,tσj,tCov[yi,t,yj,t−h]
我们能从中得到什么?
| 相关系数 | 解释 |
|---|---|
| ρ i , j ( 0 ) ≠ 0 \rho_{i,j}(0)\neq0 ρi,j(0)=0 | y i , t y_{i,t} yi,t和 y j , t y_{j,t} yj,t是同时线性相关的 |
| ρ i , j ( h ) = ρ j , i ( h ) = 0 for all h ≥ 0 \rho_{i,j}(h)=\rho_{j,i}(h)=0\text{ for all }h\geq0 ρi,j(h)=ρj,i(h)=0 for all h≥0 | y i , t y_{i,t} yi,t和 y j , t y_{j,t} yj,t没有线性关系 |
| ρ i , j ( h ) = 0 and ρ j , i ( h ) = 0 for all h > 0 \rho_{i,j}(h)=0 \text{ and } \rho_{j,i}(h)=0 \text{ for all } h>0 ρi,j(h)=0 and ρj,i(h)=0 for all h>0 | y i , t y_{i,t} yi,t和 y j , t y_{j,t} yj,t称为线性不耦合 |
| ρ i , j ( h ) = 0 \rho_{i,j}(h)=0 ρi,j(h)=0 for all h > 0 h\gt 0 h>0,but ρ j , i ( q ) ≠ 0 \rho_{j,i}(q)\neq 0 ρj,i(q)=0 for at least some q > 0 q\gt 0 q>0 | y i , t y_{i,t} yi,t和 y j , t y_{j,t} yj,t之间存在单向(线性)关系,在哪里 y i , t y_{i,t} yi,t不依赖于 y j , t y_{j,t} yj,t, 但 y j , t y_{j,t} yj,t取决于(一些)滞后值 y i , t y_{i,t} yi,t |
| ρ i , j ( h ) ≠ 0 \rho_{i,j}(h)\neq0 ρi,j(h)=0 for at least some h > 0 h>0 h>0 and ρ j , i ( q ) ≠ 0 \rho_{j,i}(q)\neq0 ρj,i(q)=0 for at least some q > 0 q>0 q>0 | 𝑦 𝑖 , 𝑡 𝑦_{𝑖,𝑡} yi,t和 𝑦 𝑗 , 𝑡 𝑦_{𝑗,𝑡} yj,t之间存在双向(反馈)线性关系。 |
Vector Autoregressive (VAR) Models
向量自回归(VAR)模型是分析多元时间序列最成功的模型之一。 事实证明,它能成功地描述经济和金融时间序列的关系并进行预测,与单变量时间序列模型和基于理论的同时方程模型相比,它能提供更准确的预测。
VAR 模型的结构只是单变量 AR 模型的一般化。 它是一个系统回归模型,将所有变量视为内生变量,并允许每个变量依赖于自身和系统中所有其他变量的𝑝滞后值。
p
p
p阶的VAR模型可以表示为:
y
t
=
a
0
+
A
1
y
t
−
1
+
A
2
y
t
−
2
+
…
+
A
p
y
t
−
p
+
u
t
=
a
0
+
∑
j
=
1
p
A
j
y
t
−
j
+
u
t
\mathbf{y}_t=\mathbf{a}_0+\mathbf{A}_1\mathbf{y}_{t-1}+\mathbf{A}_2\mathbf{y}_{t-2}+\ldots+\mathbf{A}_p\mathbf{y}_{t-p}+\mathbf{u}_t=\mathbf{a}_0+\sum_{j=1}^p\mathbf{A}_j\mathbf{y}_{t-j}+\mathbf{u}_t
yt=a0+A1yt−1+A2yt−2+…+Apyt−p+ut=a0+j=1∑pAjyt−j+ut
其中
y
t
y_t
yt是
N
×
1
N\times 1
N×1的向量包含
N
N
N个内生性变量,
a
0
a_0
a0是
N
×
1
N\times 1
N×1维的常数,
A
1
,
A
2
,
…
,
A
p
\mathbf{A}_{1},\mathbf{A}_{2},\ldots,\mathbf{A}_{p}
A1,A2,…,Ap是
p
N
×
N
pN\times N
pN×N维度的自相关系数矩阵,
μ
t
\mu_t
μt是
N
×
1
N\times 1
N×1维度的白噪声扰动项。
VAR(1) Model
为了简单我们考虑最简单的VAR模型 p = 1 p=1 p=1。
Structural and Reduced Forms of the VAR model
考虑以下二元系统
y
1
,
t
=
b
1
,
0
−
b
1
,
2
y
2
,
t
+
φ
1
,
1
y
1
,
t
−
1
+
φ
1
,
2
y
2
,
t
−
1
+
ε
1
,
t
y
2
,
t
=
b
2
,
0
−
b
2
,
1
y
2
,
t
+
φ
2
,
1
y
1
,
t
−
1
+
φ
2
,
2
y
2
,
t
−
1
+
ε
2
,
t
y_{1,t}=b_{1,0}-b_{1,2}y_{2,t}+\varphi_{1,1}y_{1,t-1}+\varphi_{1,2}y_{2,t-1}+\varepsilon_{1,t}\\y_{2,t}=b_{2,0}-b_{2,1}y_{2,t}+\varphi_{2,1}y_{1,t-1}+\varphi_{2,2}y_{2,t-1}+\varepsilon_{2,t}
y1,t=b1,0−b1,2y2,t+φ1,1y1,t−1+φ1,2y2,t−1+ε1,ty2,t=b2,0−b2,1y2,t+φ2,1y1,t−1+φ2,2y2,t−1+ε2,t
其中
y
1
,
t
y_{1,t}
y1,t和
y
2
,
t
y_{2,t}
y2,t被认为是平稳的,而且
ϵ
1
,
t
\epsilon_{1,t}
ϵ1,t和
ϵ
2
,
t
\epsilon_{2,t}
ϵ2,t分别是标准差为
σ
1
,
𝑡
\sigma_{1,𝑡}
σ1,t 和
σ
2
,
𝑡
\sigma_{2,𝑡}
σ2,t 的不相关误差项。
用矩阵符号表示
[
1
b
1
,
2
b
2
,
1
1
]
[
y
1
,
t
y
2
,
t
]
=
[
b
1
,
0
b
2
,
0
]
+
[
φ
1
,
1
φ
1
,
2
φ
2
,
1
φ
2
,
2
]
[
y
1
,
t
−
1
y
2
,
t
−
1
]
+
[
ε
1
,
t
ε
2
,
t
]
\begin{bmatrix}1&b_{1,2}\\b_{2,1}&1\end{bmatrix}\begin{bmatrix}y_{1,t}\\y_{2,t}\end{bmatrix}=\begin{bmatrix}b_{1,0}\\b_{2,0}\end{bmatrix}+\begin{bmatrix}\varphi_{1,1}&\varphi_{1,2}\\\varphi_{2,1}&\varphi_{2,2}\end{bmatrix}\begin{bmatrix}y_{1,t-1}\\y_{2,t-1}\end{bmatrix}+\begin{bmatrix}\varepsilon_{1,t}\\\varepsilon_{2,t}\end{bmatrix}
[1b2,1b1,21][y1,ty2,t]=[b1,0b2,0]+[φ1,1φ2,1φ1,2φ2,2][y1,t−1y2,t−1]+[ε1,tε2,t]
令:
B
≡
[
1
b
1
,
2
b
2
,
1
1
]
,
y
t
≡
[
y
1
,
t
y
2
,
t
]
,
Q
0
≡
[
b
1
,
0
b
2
,
0
]
,
Q
1
≡
[
φ
1
,
1
φ
1
,
2
φ
2
,
1
φ
2
,
2
]
,
y
t
−
1
≡
[
y
1
,
t
−
1
y
2
,
t
−
1
]
,
ε
t
≡
[
ε
1
,
t
ε
2
,
t
]
\begin{aligned}\mathbf{B}\equiv\left[\begin{array}{cc}1&b_{1,2}\\b_{2,1}&1\end{array}\right],\mathbf{y}_{t}\equiv\left[\begin{array}{cc}y_{1,t}\\y_{2,t}\end{array}\right],\mathbf{Q}_{0}\equiv\left[\begin{array}{cc}b_{1,0}\\b_{2,0}\end{array}\right],\mathbf{Q}_{1}\equiv\left[\begin{array}{cc}\varphi_{1,1}&\varphi_{1,2}\\\varphi_{2,1}&\varphi_{2,2}\end{array}\right],\\\mathbf{y}_{t-1}\equiv\left[\begin{array}{cc}y_{1,t-1}\\y_{2,t-1}\end{array}\right],\varepsilon_{t}\equiv\left[\begin{array}{cc}\varepsilon_{1,t}\\\varepsilon_{2,t}\end{array}\right]\end{aligned}
B≡[1b2,1b1,21],yt≡[y1,ty2,t],Q0≡[b1,0b2,0],Q1≡[φ1,1φ2,1φ1,2φ2,2],yt−1≡[y1,t−1y2,t−1],εt≡[ε1,tε2,t]
之后:
B
y
t
=
Q
0
+
Q
1
y
t
−
1
+
ε
t
\mathbf{B}\mathbf{y}_t=\mathbf{Q}_0+\mathbf{Q}_1\mathbf{y}_{t-1}+\boldsymbol{\varepsilon}_t
Byt=Q0+Q1yt−1+εt
结构 VAR(原始形式的 VAR)
- 由上式描述
- 捕获同期反馈效应 ( b 1 , 2 , b 2 , 1 ) (b_{1,2},b_{2,1}) (b1,2,b2,1)
- 使用起来不是很实用
- 同期项不能用于预测
- 需要进一步处理才能使其更有用(如将矩阵方程乘以 𝐵 − 1 𝐵^{-1} B−1)
将矩阵方程乘以
𝐵
−
1
𝐵^{-1}
B−1,我们得到
y
t
=
a
0
+
A
1
y
t
−
1
+
u
t
\mathbf{y}_t=\mathbf{a}_0+\mathbf{A}_1\mathbf{y}_{t-1}+\mathbf{u}_t
yt=a0+A1yt−1+ut
或者
y
t
=
a
0
+
A
1
L
y
t
+
u
t
\mathbf{y}_t=\mathbf{a}_0+\mathbf{A}_1L\mathbf{y}_t+\mathbf{u}_t
yt=a0+A1Lyt+ut
其中,
a
0
=
B
−
1
Q
0
\mathbf{a}_0=\mathbf{B}^{-1}\mathbf{Q}_0
a0=B−1Q0,
A
1
=
B
−
1
Q
1
\mathbf{A}_{1}=\mathbf{B}^{-1}\mathbf{Q}_{1}
A1=B−1Q1,
𝐿
𝐿
L 是滞后/后移算子,
u
t
=
B
−
1
ε
t
\mathbf{u}_t=\mathbf{B}^{-1}\boldsymbol{\varepsilon}_t
ut=B−1εt,等价、
y
1
,
t
=
a
1
,
0
+
a
1
,
1
y
1
,
t
−
1
+
a
1
,
2
y
2
,
t
−
1
+
u
1
,
t
y
2
,
t
=
a
2
,
0
+
a
2
,
1
y
1
,
t
−
1
+
a
2
,
2
y
2
,
t
−
1
+
u
2
,
t
y_{1,t}=a_{1,0}+a_{1,1}y_{1,t-1}+a_{1,2}y_{2,t-1}+u_{1,t}\\y_{2,t}=a_{2,0}+a_{2,1}y_{1,t-1}+a_{2,2}y_{2,t-1}+u_{2,t}
y1,t=a1,0+a1,1y1,t−1+a1,2y2,t−1+u1,ty2,t=a2,0+a2,1y1,t−1+a2,2y2,t−1+u2,t
简化的VAR模型(VAR 的标准形式)
- 如上所述
- 仅取决于滞后的内生变量(无同期反馈)
- 可使用普通最小二乘法 (OLS) 进行估计
VMA 无限表示法和固定性
考虑简化形式的标准 VAR(1)模型
y
t
=
a
0
+
A
1
y
t
−
1
+
u
t
\mathbf{y}_t=\mathbf{a}_0+\mathbf{A}_1\mathbf{y}_{t-1}+\mathbf{u}_t
yt=a0+A1yt−1+ut
假设过程是弱静止的,并求取
𝑦
𝑡
𝑦_𝑡
yt 的期望值,我们得到
E
[
y
t
]
=
a
0
+
A
1
E
[
y
t
−
1
]
E\left[\mathbf{y}_t\right]=\mathbf{a}_0+\mathbf{A}_1E\left[\mathbf{y}_{t-1}\right]
E[yt]=a0+A1E[yt−1]
其中
E
[
u
t
]
=
0
E\left[\mathbf{u}_{t}\right]=0
E[ut]=0。如果我们让
y
~
t
≡
y
t
−
μ
\tilde{\mathbf{y}}_t\equiv\mathbf{y}_t-\boldsymbol{\mu}
y~t≡yt−μ为均值校正后的时间序列,我们可以将模型写成
y
~
t
=
A
1
y
~
t
−
1
+
u
t
\tilde{\mathbf{y}}_t=\mathbf{A}_1\tilde{\mathbf{y}}_{t-1}+\mathbf{u}_t
y~t=A1y~t−1+ut
代入
y
~
t
−
1
=
A
1
y
~
t
−
2
+
u
t
−
1
\tilde{\mathbf{y}}_{t-1}=\mathbf{A}_1\tilde{\mathbf{y}}_{t-2}+\mathbf{u}_{t-1}
y~t−1=A1y~t−2+ut−1,
y
~
t
=
A
1
(
A
1
y
~
t
−
2
+
u
t
−
1
)
+
u
t
\tilde{\mathbf{y}}_t=\mathbf{A}_1\left(\mathbf{A}_1\tilde{\mathbf{y}}_{t-2}+\mathbf{u}_{t-1}\right)+\mathbf{u}_t
y~t=A1(A1y~t−2+ut−1)+ut
如果继续迭代,我们会得到
y
t
=
μ
+
∑
i
=
1
∞
A
1
i
u
t
−
i
+
u
t
\mathbf{y}_t=\boldsymbol{\mu}+\sum_{i=1}^\infty\mathbf{A}_1^i\mathbf{u}_{t-i}+\mathbf{u}_t
yt=μ+i=1∑∞A1iut−i+ut
令
Θ
i
≡
A
1
i
\Theta_i\equiv A_1^i
Θi≡A1i,我们得到 VMA 的无限表示
y
t
=
μ
+
∑
i
=
1
∞
Θ
i
u
t
−
i
+
u
t
\mathbf{y}_t=\boldsymbol{\mu}+\sum_{i=1}^\infty\boldsymbol{\Theta}_i\mathbf{u}_{t-i}+\mathbf{u}_t
yt=μ+i=1∑∞Θiut−i+ut
Stationarity of the VAR(1) model
- 矩阵 A 1 A_1 A1 的所有 N 个特征值的模必须小于 1,以避免系数矩阵 𝐴 1 𝑗 𝐴_1^𝑗 A1j 在 𝑗 𝑗 j 变为无穷大时爆炸或收敛为非零矩阵。
- 只要 𝑢 𝑡 𝑢_𝑡 ut 的协方差矩阵存在, 𝐴 1 𝐴_1 A1 的所有特征值的模值都小于 1 的要求就是 𝑦 𝑡 𝑦_𝑡 yt 稳定的必要条件和充分条件,因此也是静止条件。
- d e t ( I N − A 1 z ) = 0 det\left(\mathbf{I}_N-\mathbf{A}_1z\right)=0 det(IN−A1z)=0的所有根必须位于单位圆之外。
VAR§ Model
考虑以下描述的 VAR(p)模型
y
t
=
a
0
+
A
1
y
t
−
1
+
A
2
y
t
−
2
+
…
+
A
p
y
t
−
p
+
u
t
=
a
0
+
∑
j
=
1
p
A
j
y
t
−
j
+
u
t
\mathbf{y}_t=\mathbf{a}_0+\mathbf{A}_1\mathbf{y}_{t-1}+\mathbf{A}_2\mathbf{y}_{t-2}+\ldots+\mathbf{A}_p\mathbf{y}_{t-p}+\mathbf{u}_t=\mathbf{a}_0+\sum_{j=1}^p\mathbf{A}_j\mathbf{y}_{t-j}+\mathbf{u}_t
yt=a0+A1yt−1+A2yt−2+…+Apyt−p+ut=a0+j=1∑pAjyt−j+ut
利用滞后算子
𝐿
𝐿
L ,我们得到
A
~
(
L
)
y
t
=
a
0
+
u
t
\tilde{\mathbf{A}}(L)\mathbf{y}_t=\mathbf{a}_0+\mathbf{u}_t
A~(L)yt=a0+ut
其中
A
~
(
L
)
=
(
I
N
−
A
1
L
−
…
−
A
p
L
p
)
\tilde{\mathbf{A}}(L)=(\mathbf{I}_N-A_1L-\ldots-A_pL^p)
A~(L)=(IN−A1L−…−ApLp)。假设
y
t
\mathbf{y}_{t}
yt是弱平稳的,我们得到
μ
=
E
[
y
t
]
=
(
I
N
−
A
1
L
−
…
−
A
p
L
p
)
−
1
a
0
\boldsymbol{\mu}=E[\mathbf{y}_t]=(\mathbf{I}_N-A_1L-\ldots-A_pL^p)^{-1}\mathbf{a}_0
μ=E[yt]=(IN−A1L−…−ApLp)−1a0
定义
y
~
t
=
y
t
−
μ
\tilde{\mathbf{y}}_t=\mathbf{y}_t-\boldsymbol{\mu}
y~t=yt−μ,我们有
y
~
t
=
A
1
y
~
t
−
1
+
A
2
y
~
t
−
2
+
…
+
A
p
y
~
t
−
p
+
u
t
\tilde{\mathbf{y}}_t=\mathbf{A}_1\tilde{\mathbf{y}}_{t-1}+\mathbf{A}_2\tilde{\mathbf{y}}_{t-2}+\ldots+\mathbf{A}_p\tilde{\mathbf{y}}_{t-p}+\mathbf{u}_t
y~t=A1y~t−1+A2y~t−2+…+Apy~t−p+ut
Properties
- C o v [ y t , u t ] = Σ u Cov[\mathbf{y}_t,\mathbf{u}_t]=\Sigma_u Cov[yt,ut]=Σu, μ t \mu_t μt的协方差矩阵。
- C o v [ y t − h , u t ] = 0 for any h > 0 Cov[\mathbf{y}_{t-h},\mathbf{u}_t]=\mathbf{0}\text{ for any }h>0 Cov[yt−h,ut]=0 for any h>0。
- Γ h = A 1 Γ h − 1 + … + A p Γ h − p for h > 0 \mathbf{\Gamma}_h=\mathbf{A}_1\mathbf{\Gamma}_{h-1}+\ldots+\mathbf{A}_p\mathbf{\Gamma}_{h-p}\text{ for }h>0 Γh=A1Γh−1+…+ApΓh−p for h>0
- ρ h = Ψ 1 Γ h − 1 + … + Ψ p Γ h − p for h > 0 \rho_h=\Psi_1\Gamma_{h-1}+\ldots+\Psi_p\Gamma_{h-p}\text{ for }h>0 ρh=Ψ1Γh−1+…+ΨpΓh−p for h>0, where Ψ i = D − 1 / 2 A i D − 1 / 2 \mathbf{\Psi}_i=\mathbf{D}^{-1/2}\mathbf{A}_iD^{-1/2} Ψi=D−1/2AiD−1/2。
Stationarity of VAR§ model
- d e t ( I N − A 1 z − … − A p z p ) = 0 det\left(\mathbf{I}_{N}-\mathbf{A}_{1}z-\ldots-\mathbf{A}_{p}z^{p}\right)=0 det(IN−A1z−…−Apzp)=0 的所有根必须位于单位圆之外。
Specification of a VAR model: Choosing the order p p p
拟合 VAR 模型需要选择一个参数:模型阶次或滞后长度𝑝。 选择最佳模型的最常见方法是选择
𝑝
𝑝
p,使在一系列模型阶次中评估的一个或多个信息标准最小化。 该标准由两部分组成:第一部分表征熵率或预测误差,第二部分表征模型中自由估计参数的数量。 最小化这两个项将使我们能够确定一个既能准确模拟数据,又能防止过拟合(由于参数过多)的模型。
常用的信息标准包括 阿凯克信息准则 (AIC)、施瓦茨贝叶斯信息准则 (BIC)、汉南-奎因准则 (HQ) 和阿凯克最终预测误差准则 (FPE)。 各标准的计算公式如下。
Akaike’s information criterion:
(
M
)
AIC
=
ln
∣
Σ
~
u
∣
+
2
k
T
(M)\operatorname{AIC}=\ln|\tilde{\boldsymbol{\Sigma}}_u|+2\frac{k}{T}
(M)AIC=ln∣Σ~u∣+2Tk
Schwarz’s Bayesian information criterion
(
M
)
BIC
=
ln
∣
Σ
~
u
∣
+
k
T
l
n
(
T
)
(M)\operatorname{BIC}=\ln|\tilde{\boldsymbol{\Sigma}}_u|+\frac{k}{T}\mathrm{ln}(T)
(M)BIC=ln∣Σ~u∣+Tkln(T)
Hannan-Quinn’s information criterion
(
M
)
HQIC
=
ln
∣
Σ
~
u
∣
+
k
T
ln
(
ln
(
T
)
)
(M)\operatorname{HQIC}=\ln|\tilde{\boldsymbol{\Sigma}}_u|+\frac{k}{T}\ln(\ln(T))
(M)HQIC=ln∣Σ~u∣+Tkln(ln(T))
Final prediction error
F
P
E
(
p
)
=
(
T
+
N
p
+
1
T
−
N
p
+
1
)
N
∣
Σ
~
u
∣
ln
(
F
P
E
(
p
)
)
=
ln
∣
Σ
~
u
∣
+
N
ln
(
T
+
N
p
+
1
T
−
N
p
+
1
)
\mathrm{FPE}(p)=\left(\frac{T+Np+1}{T-Np+1}\right)^N|\tilde{\Sigma}_u|\\\ln(\mathrm{FPE}(p))=\ln|\tilde{\boldsymbol{\Sigma}}_u|+N\ln\left(\frac{T+Np+1}{T-Np+1}\right)
FPE(p)=(T−Np+1T+Np+1)N∣Σ~u∣ln(FPE(p))=ln∣Σ~u∣+Nln(T−Np+1T+Np+1)
其中,
𝑀
𝑀
M代表多变量,
Σ
~
u
\tilde\Sigma_u
Σ~u是估计的残差协方差矩阵,
𝑇
𝑇
T是样本中的观测值个数,
𝑘
𝑘
k是
V
A
R
(
𝑝
)
VAR(𝑝)
VAR(p)中方程的总个数(即:
N
2
p
+
N
N^{2}p+N
N2p+N)。即
N
2
p
+
N
N^{2}p+N
N2p+N,其中
𝑁
𝑁
N 是方程数,
𝑝
𝑝
p 是滞后数)。
在上述指标中,AIC 和 BIC 是使用最广泛的标准,但 BIC 对高阶的惩罚更大。 对于中等和大样本量,AIC 和 FPE 基本相当,但对于小样本量,FPE 可能优于 AIC。 HQ 对高阶模型的惩罚也比 AIC 重,但比 BIC 轻。 然而,在小样本条件下,AIC/FPE 在选择真实模型阶次方面可能优于 BIC 和/或 HQ。
在某些情况下,AIC 和 FPE 在一定的模型阶数或滞后长度范围内没有显示出明显的最小值。 在这种情况下,当我们绘制模型阶次的数值时,可能会出现一个明显的 “弯头”。 这可能表明有合适的模型阶数。
Building a VAR model
在本节中,我们将展示如何使用 VAR 模型来预测空气质量数据。 具体步骤如下:
- 检查平稳性
- 将数据分为训练集和测试集
- 选择能给出的VAR阶数p
- 在训练集上拟合阶数为 p p p的VAR模型
- 生成预测
- 评估模型性能
Example 2: Forecasting Air Quality Data (CO, NO2 and RH)
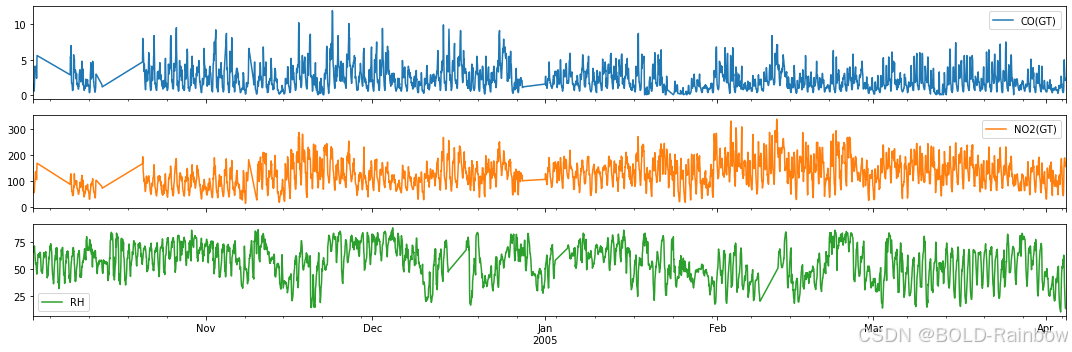
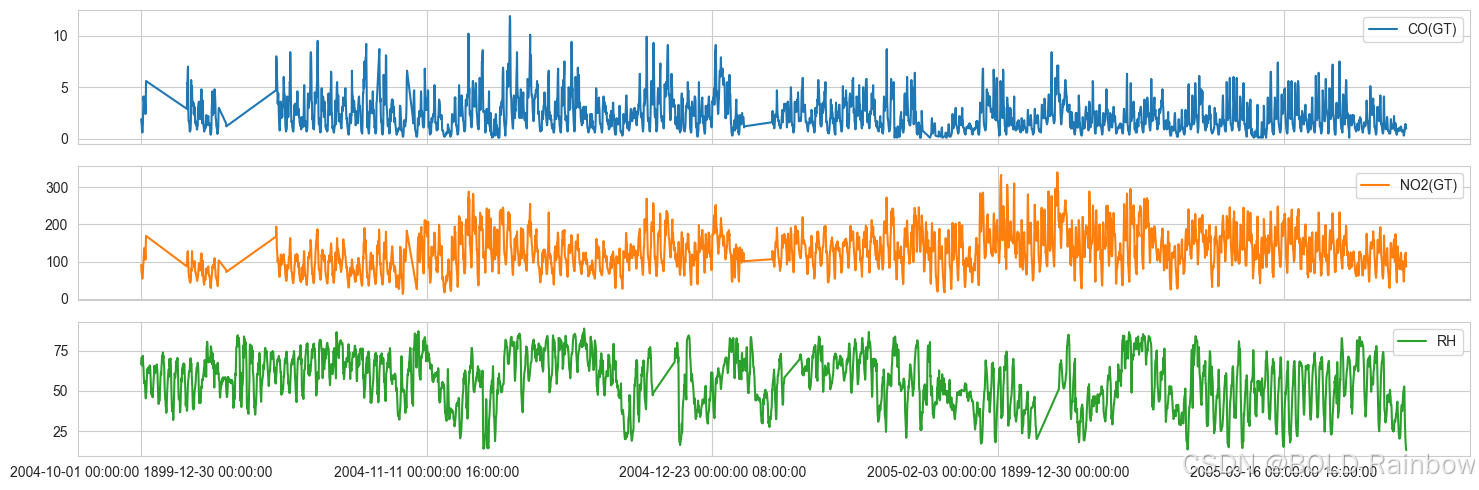
为了说明问题,我们考虑了 2014 年 10 月 1 日空气质量数据集中的一氧化碳、二氧化氮和相对湿度时间序列。
cols = ['CO(GT)', 'NO2(GT)', 'RH']
data_df = aq_df.loc[aq_df.index>'2004-10-01',cols]
fig,ax = plt.subplots(3, figsize=(15,5), sharex=True)
data_df.plot(ax=ax, subplots=True)
plt.xlabel('')
plt.tight_layout()
plt.show()
在进行建模之前,我们先快速检查一下…
为了弄清多变量方法是否比将信号作为单变量时间序列单独处理更好,我们使用 CCF 检验了变量之间的关系。 下面的示例显示了一氧化碳、二氧化氮和相对湿度的空气质量数据最近 100 个数据点的 CCF。
CO 和
N
O
2
NO_2
NO2
sample_df = data_df.iloc[-100:]
ccf_y1_y2 = ccf(sample_df['CO(GT)'], sample_df['NO2(GT)'], unbiased=False)
ccf_y2_y1 = ccf(sample_df['NO2(GT)'], sample_df['CO(GT)'], unbiased=False)
fig, ax = plt.subplots(2, figsize=(15, 4), sharex=True, sharey=True)
d=1
ax[0].stem(np.arange(len(sample_df))[::d], ccf_y1_y2[::d], linefmt='C1-', markerfmt='C1o')
ax[1].stem(np.arange(len(sample_df))[::d], ccf_y2_y1[::d], linefmt='C1-', markerfmt='C1o')
ax[-1].set_ylim(-1, 1)
ax[0].set_xlim(0, 100)
ax[-1].set_xlabel('lag $h$', fontsize=14)
ax[0].set_ylabel(r'$\rho_{CO,NO2} (h)$', fontsize=14)
ax[1].set_ylabel(r'$\rho_{NO2,CO} (h)$', fontsize=14)
plt.tight_layout()
plt.show()
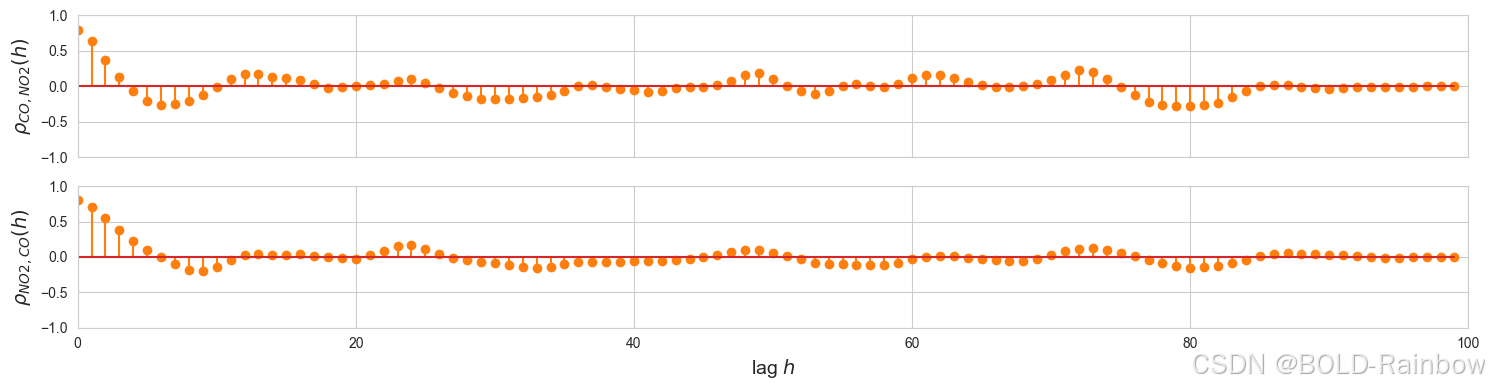
CO 和 RH
ccf_y1_y2 = ccf(sample_df['CO(GT)'], sample_df['RH'], unbiased=False)
ccf_y2_y1 = ccf(sample_df['RH'], sample_df['CO(GT)'], unbiased=False)
fig, ax = plt.subplots(2, figsize=(15, 4), sharex=True, sharey=True)
d=1
ax[0].stem(np.arange(len(sample_df))[::d], ccf_y1_y2[::d], linefmt='C1-', markerfmt='C1o')
ax[1].stem(np.arange(len(sample_df))[::d], ccf_y2_y1[::d], linefmt='C1-', markerfmt='C1o')
ax[-1].set_ylim(-1, 1)
ax[0].set_xlim(0, 100)
ax[-1].set_xlabel('lag $h$', fontsize=14)
ax[0].set_ylabel(r'$\rho_{CO,RH} (h)$', fontsize=14)
ax[1].set_ylabel(r'$\rho_{RH,CO} (h)$', fontsize=14)
plt.tight_layout()
plt.show()
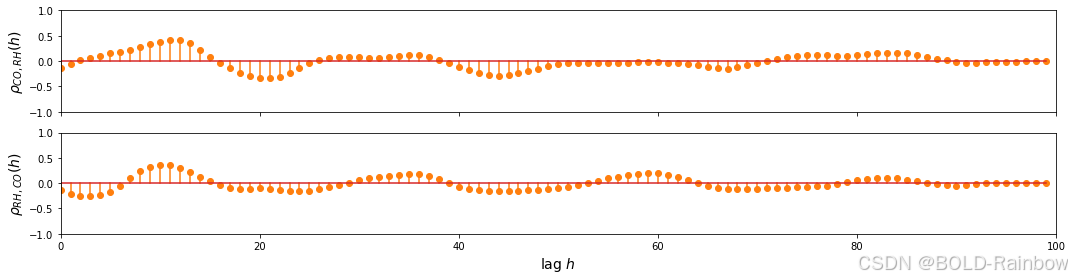
RH and NO2
ccf_y1_y2 = ccf(sample_df['RH'], sample_df['NO2(GT)'], unbiased=False)
ccf_y2_y1 = ccf(sample_df['NO2(GT)'], sample_df['RH'], unbiased=False)
fig, ax = plt.subplots(2, figsize=(15, 4), sharex=True, sharey=True)
d=1
ax[0].stem(np.arange(len(sample_df))[::d], ccf_y1_y2[::d], linefmt='C1-', markerfmt='C1o')
ax[1].stem(np.arange(len(sample_df))[::d], ccf_y2_y1[::d], linefmt='C1-', markerfmt='C1o')
ax[-1].set_ylim(-1, 1)
ax[0].set_xlim(0, 100)
ax[-1].set_xlabel('lag $h$', fontsize=14)
ax[0].set_ylabel(r'$\rho_{RH,NO2} (h)$', fontsize=14)
ax[1].set_ylabel(r'$\rho_{NO2,RH} (h)$', fontsize=14)
plt.tight_layout()
plt.show()
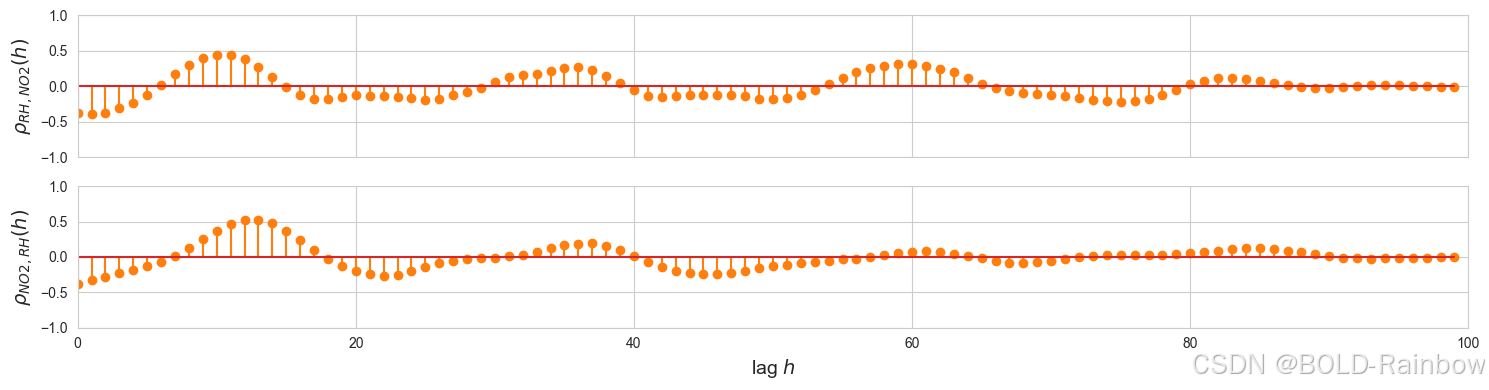
Observation/s
如上图所示,我们可以看到以下两者之间的关系:
- C O CO CO以及相对湿度和 N O 2 NO_2 NO2的一些滞后值
- N O 2 NO_2 NO2和 R H RH RH和 C O CO CO的滞后值
- 相对湿度以及 CO 和 NO2 的一些滞后值
这表明我们可以从多元方法中获益,因此我们继续建立 VAR 模型。
Check stationarity
为了检查静态性,我们使用了 Kwiatkowski-Phillips-Schmidt-Shin(KPSS)检验和 Augmented Dickey-Fuller (ADF)检验。 要使数据适合 VAR 建模,我们需要多元时间序列中的每个变量都是静态的。 在这两种检验中,我们都需要检验统计量小于临界值,才能说时间序列(变量)是静态的。
Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test
回顾一下: 零假设是指可观测的时间序列围绕一个确定性趋势(即趋势-静态)是静止的,而另一个假设是单位根。
test_stat, p_val = [], []
cv_1pct, cv_2p5pct, cv_5pct, cv_10pct = [], [], [], []
for c in data_df.columns:
kpss_res = kpss(data_df[c].dropna(), regression='ct')
test_stat.append(kpss_res[0])
p_val.append(kpss_res[1])
cv_1pct.append(kpss_res[3]['1%'])
cv_2p5pct.append(kpss_res[3]['1%'])
cv_5pct.append(kpss_res[3]['5%'])
cv_10pct.append(kpss_res[3]['10%'])
kpss_res_df = pd.DataFrame({'Test statistic': test_stat,
'p-value': p_val,
'Critical value - 1%': cv_1pct,
'Critical value - 2.5%': cv_2p5pct,
'Critical value - 5%': cv_5pct,
'Critical value - 10%': cv_10pct},
index=data_df.columns).T
kpss_res_df.round(4)
| CO(GT) | NO2(GT) | RH |
|---|---|---|
| Test statistic | 0.0702 | 0.3239 |
| p-value | 0.1000 | 0.0100 |
| Critical value - 1% | 0.2160 | 0.2160 |
| Critical value - 2.5% | 0.2160 | 0.2160 |
| Critical value - 5% | 0.1460 | 0.1460 |
| Critical value - 10% | 0.1190 | 0.1190 |
Observation/s:根据 KPSS 检验,一氧化碳和相对湿度是静态的。
Augmented Dickey-Fuller (ADF) test
召回: 零假设是时间序列样本中存在单位根,而另一假设是时间序列是静止的。
test_stat, p_val = [], []
cv_1pct, cv_5pct, cv_10pct = [], [], []
for c in data_df.columns:
adf_res = adfuller(data_df[c].dropna())
test_stat.append(adf_res[0])
p_val.append(adf_res[1])
cv_1pct.append(adf_res[4]['1%'])
cv_5pct.append(adf_res[4]['5%'])
cv_10pct.append(adf_res[4]['10%'])
adf_res_df = pd.DataFrame({'Test statistic': test_stat,
'p-value': p_val,
'Critical value - 1%': cv_1pct,
'Critical value - 5%': cv_5pct,
'Critical value - 10%': cv_10pct},
index=data_df.columns).T
adf_res_df.round(4)
| GO(GT) | NO2(GT) | RH | |
|---|---|---|---|
| Test statistic | -7.0195 | -6.7695 | -6.8484 |
| p-value | 0.0000 | 0.0000 | 0.0000 |
| Critical value - 1% | -3.4318 | -3.4318 | -3.4318 |
| Critical value - 5% | -2.8622 | -2.8622 | -2.8622 |
| Critical value - 10% | -2.5671 | -2.5671 | -2.5671 |
Observation/s:根据 ADF 检验,一氧化碳、二氧化氮和相对湿度是静态的。
2.Split data into train and test sets
我们使用 2014 年 10 月 1 日的数据集来预测数据集中的最后 24 个点(24 小时/1 天)。
forecast_length = 24
train_df, test_df = data_df.iloc[:-forecast_length], data_df.iloc[-forecast_length:]
test_df = test_df.filter(test_df.columns[~test_df.columns.str.contains('-d')])
train_df.reset_index().to_csv('../data/AirQualityUCI/train_data.csv')
test_df.reset_index().to_csv('../data/AirQualityUCI/test_data.csv')
fig,ax = plt.subplots(3, figsize=(15, 5), sharex=True)
train_df.plot(ax=ax, subplots=True)
plt.xlabel('')
plt.tight_layout()
plt.show()
Select order p
我们计算不同的多元信息标准(AIC、BIC、HQIC)和 FPE。 我们选取数值最低的一组阶次参数。
aic, bic, fpe, hqic = [], [], [], []
model = VAR(train_df)
p = np.arange(1,60)
for i in p:
result = model.fit(i)
aic.append(result.aic)
bic.append(result.bic)
fpe.append(result.fpe)
hqic.append(result.hqic)
lags_metrics_df = pd.DataFrame({'AIC': aic,
'BIC': bic,
'HQIC': hqic,
'FPE': fpe},
index=p)
fig, ax = plt.subplots(1, 4, figsize=(15, 3), sharex=True)
lags_metrics_df.plot(subplots=True, ax=ax, marker='o')
plt.tight_layout()

Obervations:
我们发现𝑝=26 时的 BIC 和 HQIC 最低,而且我们还观察到 AIC 和 FPE 的图中出现了一个弯头,因此我们选择滞后期数为 26。
Fit VAR model with chosen order
%%time
var_model = model.fit(26)
var_model.summary()
CPU times: user 401 ms, sys: 39.9 ms, total: 441 ms
Wall time: 202 ms
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Sun, 21, Feb, 2021
Time: 00:47:42
--------------------------------------------------------------------
No. of Equations: 3.00000 BIC: 7.42717
Nobs: 4404.00 HQIC: 7.20458
Log likelihood: -34107.4 FPE: 1191.88
AIC: 7.08328 Det(Omega_mle): 1129.97
--------------------------------------------------------------------
Results for equation CO(GT)
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const 0.241332 0.069966 3.449 0.001
L1.CO(GT) 0.961418 0.019229 49.999 0.000
L1.NO2(GT) 0.001992 0.000713 2.794 0.005
L1.RH 0.009321 0.002735 3.409 0.001
L2.CO(GT) -0.279491 0.026156 -10.686 0.000
L2.NO2(GT) 0.000661 0.000970 0.682 0.495
L2.RH -0.017300 0.004278 -4.044 0.000
L3.CO(GT) 0.098032 0.026251 3.734 0.000
L3.NO2(GT) -0.000165 0.000970 -0.170 0.865
L3.RH 0.012764 0.004352 2.933 0.003
L4.CO(GT) -0.001012 0.026285 -0.038 0.969
L4.NO2(GT) -0.001148 0.000966 -1.189 0.234
L4.RH -0.006423 0.004354 -1.475 0.140
L5.CO(GT) 0.054358 0.026291 2.068 0.039
L5.NO2(GT) -0.001218 0.000966 -1.261 0.207
L5.RH 0.000664 0.004353 0.153 0.879
L6.CO(GT) -0.017663 0.026308 -0.671 0.502
L6.NO2(GT) 0.000372 0.000966 0.385 0.700
L6.RH 0.000884 0.004351 0.203 0.839
L7.CO(GT) 0.004448 0.026302 0.169 0.866
L7.NO2(GT) 0.000921 0.000967 0.953 0.340
L7.RH -0.000964 0.004353 -0.221 0.825
L8.CO(GT) -0.001457 0.026288 -0.055 0.956
L8.NO2(GT) 0.000736 0.000968 0.760 0.447
L8.RH -0.002357 0.004356 -0.541 0.588
L9.CO(GT) 0.018534 0.026296 0.705 0.481
L9.NO2(GT) -0.001551 0.000969 -1.601 0.109
L9.RH 0.004720 0.004361 1.082 0.279
L10.CO(GT) -0.003435 0.026289 -0.131 0.896
L10.NO2(GT) 0.001457 0.000969 1.503 0.133
L10.RH 0.003194 0.004366 0.732 0.464
L11.CO(GT) -0.021526 0.026286 -0.819 0.413
L11.NO2(GT) -0.001094 0.000969 -1.128 0.259
L11.RH -0.001129 0.004367 -0.259 0.796
L12.CO(GT) 0.066587 0.026287 2.533 0.011
L12.NO2(GT) -0.000285 0.000971 -0.293 0.769
L12.RH -0.002315 0.004369 -0.530 0.596
L13.CO(GT) -0.076568 0.026287 -2.913 0.004
L13.NO2(GT) 0.000551 0.000971 0.567 0.571
L13.RH 0.004622 0.004370 1.058 0.290
L14.CO(GT) 0.100874 0.026293 3.837 0.000
L14.NO2(GT) -0.003074 0.000971 -3.165 0.002
L14.RH 0.001720 0.004371 0.394 0.694
L15.CO(GT) -0.039783 0.026318 -1.512 0.131
L15.NO2(GT) 0.000926 0.000971 0.953 0.340
L15.RH -0.002928 0.004370 -0.670 0.503
L16.CO(GT) 0.009289 0.026276 0.354 0.724
L16.NO2(GT) 0.000818 0.000969 0.845 0.398
L16.RH -0.001466 0.004369 -0.336 0.737
L17.CO(GT) -0.030972 0.026264 -1.179 0.238
L17.NO2(GT) 0.000273 0.000969 0.281 0.778
L17.RH 0.000574 0.004369 0.131 0.895
L18.CO(GT) 0.021964 0.026242 0.837 0.403
L18.NO2(GT) -0.001183 0.000968 -1.222 0.222
L18.RH 0.003188 0.004366 0.730 0.465
L19.CO(GT) 0.048666 0.026200 1.858 0.063
L19.NO2(GT) -0.000539 0.000966 -0.558 0.577
L19.RH -0.010088 0.004362 -2.313 0.021
L20.CO(GT) -0.065842 0.026213 -2.512 0.012
L20.NO2(GT) 0.000847 0.000965 0.878 0.380
L20.RH 0.008736 0.004363 2.002 0.045
L21.CO(GT) -0.032047 0.026233 -1.222 0.222
L21.NO2(GT) 0.001082 0.000964 1.122 0.262
L21.RH -0.004805 0.004360 -1.102 0.270
L22.CO(GT) 0.050969 0.026220 1.944 0.052
L22.NO2(GT) -0.000471 0.000964 -0.489 0.625
L22.RH 0.000472 0.004360 0.108 0.914
L23.CO(GT) 0.071433 0.026226 2.724 0.006
L23.NO2(GT) 0.001170 0.000964 1.214 0.225
L23.RH -0.003465 0.004361 -0.794 0.427
L24.CO(GT) 0.198774 0.026160 7.598 0.000
L24.NO2(GT) -0.000280 0.000968 -0.289 0.772
L24.RH 0.001856 0.004361 0.425 0.670
L25.CO(GT) -0.156857 0.026043 -6.023 0.000
L25.NO2(GT) 0.000666 0.000967 0.689 0.491
L25.RH 0.000979 0.004290 0.228 0.820
L26.CO(GT) -0.047697 0.019186 -2.486 0.013
L26.NO2(GT) -0.001958 0.000710 -2.757 0.006
L26.RH -0.000747 0.002746 -0.272 0.786
==============================================================================
Results for equation NO2(GT)
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const 12.417213 1.871552 6.635 0.000
L1.CO(GT) 1.600229 0.514359 3.111 0.002
L1.NO2(GT) 0.953169 0.019069 49.986 0.000
L1.RH 0.239537 0.073150 3.275 0.001
L2.CO(GT) -2.404892 0.699653 -3.437 0.001
L2.NO2(GT) -0.096250 0.025935 -3.711 0.000
L2.RH -0.332820 0.114442 -2.908 0.004
L3.CO(GT) 0.154091 0.702192 0.219 0.826
L3.NO2(GT) 0.018241 0.025946 0.703 0.482
L3.RH 0.180558 0.116422 1.551 0.121
L4.CO(GT) 1.160555 0.703122 1.651 0.099
L4.NO2(GT) -0.065148 0.025831 -2.522 0.012
L4.RH -0.149770 0.116468 -1.286 0.198
L5.CO(GT) -0.209355 0.703264 -0.298 0.766
L5.NO2(GT) 0.007011 0.025834 0.271 0.786
L5.RH 0.023622 0.116443 0.203 0.839
L6.CO(GT) 0.742858 0.703728 1.056 0.291
L6.NO2(GT) -0.029688 0.025847 -1.149 0.251
L6.RH 0.014889 0.116384 0.128 0.898
L7.CO(GT) -0.535398 0.703562 -0.761 0.447
L7.NO2(GT) 0.089765 0.025857 3.472 0.001
L7.RH -0.106262 0.116432 -0.913 0.361
L8.CO(GT) -1.025553 0.703193 -1.458 0.145
L8.NO2(GT) -0.034196 0.025895 -1.321 0.187
L8.RH 0.127190 0.116517 1.092 0.275
L9.CO(GT) 0.313129 0.703395 0.445 0.656
L9.NO2(GT) 0.005236 0.025910 0.202 0.840
L9.RH -0.136264 0.116667 -1.168 0.243
L10.CO(GT) -0.507195 0.703213 -0.721 0.471
L10.NO2(GT) 0.000967 0.025922 0.037 0.970
L10.RH 0.209375 0.116786 1.793 0.073
L11.CO(GT) -1.319501 0.703135 -1.877 0.061
L11.NO2(GT) 0.069145 0.025930 2.667 0.008
L11.RH -0.053156 0.116828 -0.455 0.649
L12.CO(GT) 2.602906 0.703181 3.702 0.000
L12.NO2(GT) -0.076889 0.025968 -2.961 0.003
L12.RH -0.044469 0.116867 -0.381 0.704
L13.CO(GT) -2.098667 0.703156 -2.985 0.003
L13.NO2(GT) 0.068250 0.025986 2.626 0.009
L13.RH 0.164246 0.116893 1.405 0.160
L14.CO(GT) 1.141015 0.703317 1.622 0.105
L14.NO2(GT) -0.077485 0.025985 -2.982 0.003
L14.RH 0.121439 0.116918 1.039 0.299
L15.CO(GT) 0.157231 0.704010 0.223 0.823
L15.NO2(GT) 0.016822 0.025982 0.647 0.517
L15.RH -0.173595 0.116888 -1.485 0.138
L16.CO(GT) 0.878201 0.702861 1.249 0.211
L16.NO2(GT) 0.003234 0.025923 0.125 0.901
L16.RH -0.029109 0.116858 -0.249 0.803
L17.CO(GT) -1.418159 0.702559 -2.019 0.044
L17.NO2(GT) 0.016251 0.025913 0.627 0.531
L17.RH -0.015862 0.116863 -0.136 0.892
L18.CO(GT) 0.655452 0.701962 0.934 0.350
L18.NO2(GT) -0.021180 0.025901 -0.818 0.414
L18.RH 0.128568 0.116801 1.101 0.271
L19.CO(GT) -0.024839 0.700835 -0.035 0.972
L19.NO2(GT) 0.001731 0.025844 0.067 0.947
L19.RH -0.247871 0.116687 -2.124 0.034
L20.CO(GT) -0.810637 0.701198 -1.156 0.248
L20.NO2(GT) 0.008661 0.025806 0.336 0.737
L20.RH 0.082541 0.116699 0.707 0.479
L21.CO(GT) -0.268031 0.701722 -0.382 0.702
L21.NO2(GT) 0.006716 0.025794 0.260 0.795
L21.RH -0.148403 0.116634 -1.272 0.203
L22.CO(GT) 0.551561 0.701384 0.786 0.432
L22.NO2(GT) 0.029776 0.025786 1.155 0.248
L22.RH 0.137999 0.116639 1.183 0.237
L23.CO(GT) 0.396023 0.701541 0.565 0.572
L23.NO2(GT) 0.141030 0.025786 5.469 0.000
L23.RH -0.095500 0.116666 -0.819 0.413
L24.CO(GT) 0.359015 0.699771 0.513 0.608
L24.NO2(GT) 0.081228 0.025886 3.138 0.002
L24.RH 0.027786 0.116658 0.238 0.812
L25.CO(GT) -1.491610 0.696641 -2.141 0.032
L25.NO2(GT) -0.067370 0.025857 -2.605 0.009
L25.RH -0.015628 0.114756 -0.136 0.892
L26.CO(GT) 0.583311 0.513221 1.137 0.256
L26.NO2(GT) -0.100912 0.018999 -5.311 0.000
L26.RH 0.021928 0.073465 0.298 0.765
==============================================================================
Results for equation RH
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const 1.708989 0.393111 4.347 0.000
L1.CO(GT) -0.043025 0.108039 -0.398 0.690
L1.NO2(GT) -0.010353 0.004005 -2.585 0.010
L1.RH 1.209022 0.015365 78.688 0.000
L2.CO(GT) -0.237686 0.146959 -1.617 0.106
L2.NO2(GT) 0.010539 0.005448 1.935 0.053
L2.RH -0.290694 0.024038 -12.093 0.000
L3.CO(GT) 0.154914 0.147492 1.050 0.294
L3.NO2(GT) -0.002859 0.005450 -0.525 0.600
L3.RH 0.052192 0.024454 2.134 0.033
L4.CO(GT) 0.095980 0.147688 0.650 0.516
L4.NO2(GT) 0.003434 0.005426 0.633 0.527
L4.RH -0.021893 0.024464 -0.895 0.371
L5.CO(GT) -0.035423 0.147718 -0.240 0.810
L5.NO2(GT) -0.002389 0.005426 -0.440 0.660
L5.RH 0.037941 0.024458 1.551 0.121
L6.CO(GT) -0.040464 0.147815 -0.274 0.784
L6.NO2(GT) 0.001410 0.005429 0.260 0.795
L6.RH -0.074252 0.024446 -3.037 0.002
L7.CO(GT) -0.012767 0.147780 -0.086 0.931
L7.NO2(GT) 0.007474 0.005431 1.376 0.169
L7.RH 0.040664 0.024456 1.663 0.096
L8.CO(GT) 0.080673 0.147703 0.546 0.585
L8.NO2(GT) 0.001860 0.005439 0.342 0.732
L8.RH -0.076619 0.024474 -3.131 0.002
L9.CO(GT) 0.047686 0.147745 0.323 0.747
L9.NO2(GT) -0.004802 0.005442 -0.882 0.378
L9.RH 0.063403 0.024505 2.587 0.010
L10.CO(GT) 0.050348 0.147707 0.341 0.733
L10.NO2(GT) 0.004929 0.005445 0.905 0.365
L10.RH -0.044706 0.024530 -1.822 0.068
L11.CO(GT) 0.117202 0.147691 0.794 0.427
L11.NO2(GT) -0.002450 0.005446 -0.450 0.653
L11.RH 0.050771 0.024539 2.069 0.039
L12.CO(GT) 0.081156 0.147700 0.549 0.583
L12.NO2(GT) -0.002690 0.005454 -0.493 0.622
L12.RH -0.040349 0.024547 -1.644 0.100
L13.CO(GT) -0.028788 0.147695 -0.195 0.845
L13.NO2(GT) 0.000768 0.005458 0.141 0.888
L13.RH 0.020414 0.024553 0.831 0.406
L14.CO(GT) -0.078942 0.147729 -0.534 0.593
L14.NO2(GT) -0.002734 0.005458 -0.501 0.616
L14.RH -0.000282 0.024558 -0.011 0.991
L15.CO(GT) -0.144161 0.147874 -0.975 0.330
L15.NO2(GT) 0.002442 0.005457 0.448 0.654
L15.RH 0.030373 0.024552 1.237 0.216
L16.CO(GT) -0.001777 0.147633 -0.012 0.990
L16.NO2(GT) 0.002061 0.005445 0.379 0.705
L16.RH -0.049313 0.024546 -2.009 0.045
L17.CO(GT) 0.046799 0.147569 0.317 0.751
L17.NO2(GT) -0.007569 0.005443 -1.391 0.164
L17.RH 0.033906 0.024547 1.381 0.167
L18.CO(GT) -0.080688 0.147444 -0.547 0.584
L18.NO2(GT) 0.006073 0.005440 1.116 0.264
L18.RH 0.006116 0.024533 0.249 0.803
L19.CO(GT) 0.269110 0.147207 1.828 0.068
L19.NO2(GT) -0.004253 0.005429 -0.784 0.433
L19.RH -0.011621 0.024510 -0.474 0.635
L20.CO(GT) -0.324511 0.147284 -2.203 0.028
L20.NO2(GT) 0.000789 0.005420 0.145 0.884
L20.RH 0.041952 0.024512 1.711 0.087
L21.CO(GT) 0.177418 0.147394 1.204 0.229
L21.NO2(GT) 0.005398 0.005418 0.996 0.319
L21.RH -0.037378 0.024499 -1.526 0.127
L22.CO(GT) 0.124107 0.147323 0.842 0.400
L22.NO2(GT) -0.006135 0.005416 -1.133 0.257
L22.RH 0.041857 0.024500 1.708 0.088
L23.CO(GT) -0.041076 0.147356 -0.279 0.780
L23.NO2(GT) -0.005205 0.005416 -0.961 0.337
L23.RH 0.047960 0.024505 1.957 0.050
L24.CO(GT) 0.171936 0.146984 1.170 0.242
L24.NO2(GT) 0.003821 0.005437 0.703 0.482
L24.RH 0.010637 0.024503 0.434 0.664
L25.CO(GT) -0.302108 0.146326 -2.065 0.039
L25.NO2(GT) 0.007458 0.005431 1.373 0.170
L25.RH -0.034121 0.024104 -1.416 0.157
L26.CO(GT) 0.150202 0.107800 1.393 0.164
L26.NO2(GT) -0.008683 0.003991 -2.176 0.030
L26.RH -0.041247 0.015431 -2.673 0.008
==============================================================================
Correlation matrix of residuals
CO(GT) NO2(GT) RH
CO(GT) 1.000000 0.606004 0.150771
NO2(GT) 0.606004 1.000000 0.078143
RH 0.150771 0.078143 1.000000
4.Get forecast
forecast_var = pd.DataFrame(var_model.forecast(train_df.values,
steps=forecast_length),
columns=train_df.columns,
index=test_df.index)
forecast_var = forecast_var.rename(columns={c: c+'-VAR' for c in forecast_var.columns})
for c in train_df.columns:
fig, ax = plt.subplots(figsize=[15, 2])
pd.concat([train_df[[c]], forecast_var[[c+'-VAR']]], axis=1).plot(ax=ax)
plt.xlim(left=pd.to_datetime('2005-03-01'))
plt.xlabel('')
# plt.tight_layout()
plt.show()



Performance Evaluation: Comparison with ARIMA model
使用 ARIMA 时,我们将每个变量视为单变量时间序列,并对每个变量进行预测: 一氧化碳 1 次,二氧化氮 1 次,相对湿度 1 次
# For model order selection, refer to Chapter 1
selected_order = {'CO(GT)': [(0, 1, 0)],
'NO2(GT)': [(0, 1, 0)],
'RH': [(3, 1, 1)]}
%%time
forecast_arima = {}
for c in cols:
forecast_arima[c+'-ARIMA'] = utils.forecast_arima(train_df[c].values,
test_df[c].values,
order=selected_order[c][0])
forecast_arima = pd.DataFrame(forecast_arima, index=forecast_var.index)
forecast_arima.head()
forecasts = pd.concat([forecast_arima, forecast_var], axis=1)
for c in cols:
fig, ax = utils.plot_forecasts_static(train_df=train_df,
test_df=test_df,
forecast_df=forecasts,
column_name=c,
min_train_date='2005-04-01',
suffix=['-VAR', '-ARIMA'],
title=c)



Structural VAR Analysis
除预测外,VAR 模型还可用于结构推断和政策分析。 在宏观经济学中,这种结构分析被广泛用于研究宏观经济冲击(如货币冲击、金融冲击)的传导机制和检验经济理论。 对数据集的因果结构有特定的假设,并由此总结特定变量的意外冲击(也称为创新或扰动)对模型中不同变量的因果影响。 本节将介绍总结这些因果影响的两种常用方法:(1)脉冲响应函数;(2)预测误差方差分解。
Impulse Response Function(IRF)
- VAR 模型的系数通常难以解释,因此从业人员通常会估算脉冲响应函数。
- 脉冲响应函数(IRF)可追踪 VAR 系统中一个(或多个)内生变量受到的外生冲击对部分或全部其他变量影响的时间轨迹。
- IRF 跟踪 VAR 系统因变量对误差项冲击(也称为创新或脉冲)的响应。
IRF in the VAR system for Air Quality
让
y
1
,
t
,
y
2
,
t
y_{1,t},y_{2,t}
y1,t,y2,t和
y
3
,
t
y_{3,t}
y3,t分别为 CO 信号、NO2 信号和 RH 信号对应的时间序列。 考虑下图所示的系统移动平均表示法:
令:
[
y
1
,
t
y
2
,
t
y
3
,
t
]
=
[
μ
1
μ
2
μ
3
]
+
∑
i
=
0
∞
[
θ
1
,
1
θ
1
,
2
θ
1
,
3
θ
2
,
1
θ
2
,
2
θ
2
,
3
θ
3
,
1
θ
3
,
2
θ
3
,
3
]
[
u
1
,
t
−
i
u
2
,
t
−
i
u
3
,
t
−
i
]
\begin{bmatrix}y_{1,t}\\y_{2,t}\\y_{3,t}\end{bmatrix}=\begin{bmatrix}\mu_1\\\mu_2\\\mu_3\end{bmatrix}+\sum_{i=0}^\infty\begin{bmatrix}\theta_{1,1}&\theta_{1,2}&\theta_{1,3}\\\theta_{2,1}&\theta_{2,2}&\theta_{2,3}\\\theta_{3,1}&\theta_{3,2}&\theta_{3,3}\end{bmatrix}\begin{bmatrix}u_{1,t-i}\\u_{2,t-i}\\u_{3,t-i}\end{bmatrix}
y1,ty2,ty3,t
=
μ1μ2μ3
+i=0∑∞
θ1,1θ2,1θ3,1θ1,2θ2,2θ3,2θ1,3θ2,3θ3,3
u1,t−iu2,t−iu3,t−i
假设第一个方程中的 μ 1 \mu_1 μ1 增加了一个标准差。
- 这一冲击将改变当前和未来各期的 y 1 y_1 y1。
- 这种冲击也会对 𝑦 2 𝑦_2 y2 和 𝑦 3 𝑦_3 y3 产生影响。
假设第二个等式中的𝑢2 增加了一个标准差。
- 这一冲击将改变当前和未来各期的 𝑦 2 𝑦_2 y2。
- 这种冲击也会对 𝑦 1 𝑦_1 y1 和 𝑦 3 𝑦_3 y3 产生影响。
假设第三个等式中的 𝑢 3 𝑢_3 u3 增加了一个标准差。
- 这一冲击将改变当前和未来各期的 𝑦 3 𝑦_3 y3。
- 这种冲击也会对 𝑦 1 𝑦_1 y1 和 𝑦 2 𝑦_2 y2 产生影响。
irf = var_model.irf(periods=8)
ax = irf.plot(orth=True,
subplot_params={'fontsize': 10})
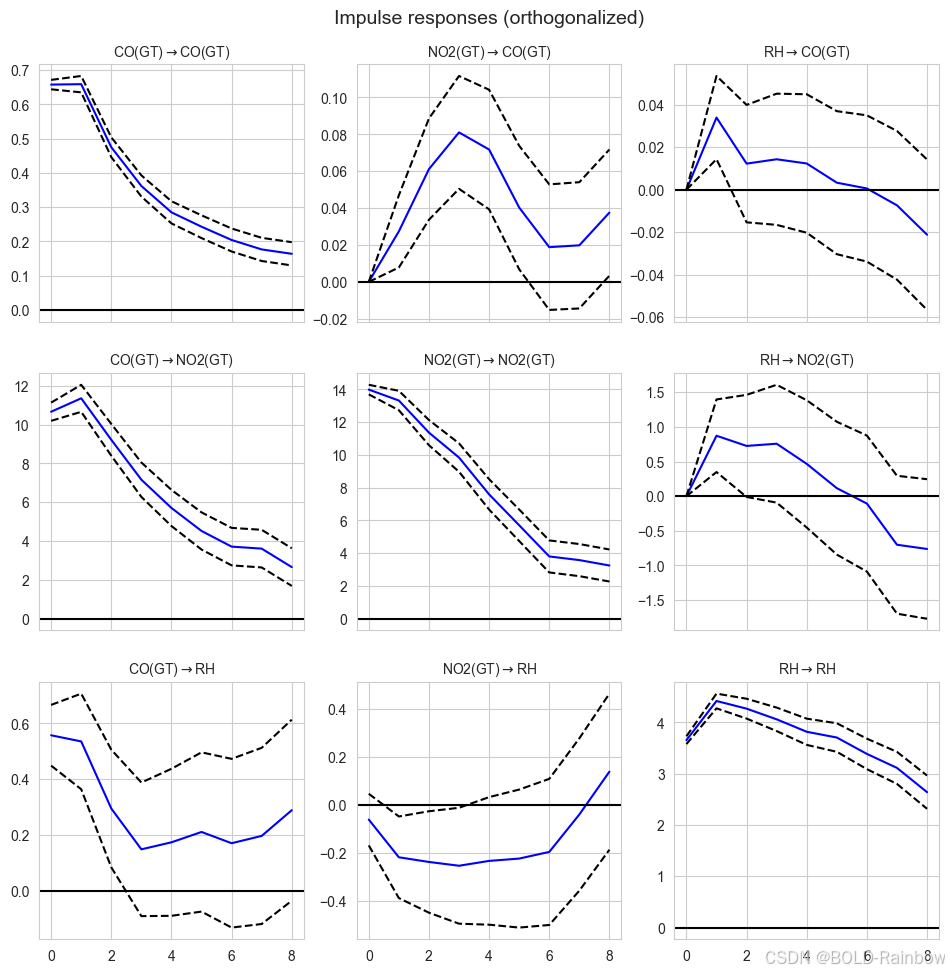
Observations
变量的外生扰动/冲击(1SD)对其自身的影响:
- 一氧化碳→CO:CO 值的冲击在凌晨时分会产生较大影响,但随着时间的推移会逐渐减弱。
- 二氧化氮→NO2:NO2 值的冲击在凌晨对 NO2 的影响较大,但随着时间的推移,这种影响会减弱。
- RH→RH:RH 值的冲击在 1 小时后对 RH 的影响最大,并且这种影响会随着时间的推移而衰减。
一个变量的外生扰动/冲击对另一个变量的影响:
- 一氧化碳→NO2:CO 值的冲击在 1 小时后对 NO2 的影响最大,并且这种影响随着时间的推移而衰减。
- 一氧化碳→RH:CO 值发生突变会立即影响 RH 值。但是,一小时后这种影响会立即减小,RH 值似乎会保持在 0.2 左右。
- 二氧化氮→CO:NO2 的冲击只会对 CO 的值造成很小的影响。似乎存在延迟效应,在 3 小时后达到峰值,但幅度仍然很小。
- 二氧化氮→RH:NO2 冲击会对 RH 值产生轻微(负面)影响。6 小时后,其幅度似乎进一步下降。IRF 值在约 7 小时内达到零。
- RH→CO:RH 冲击仅对 CO 值造成很小的影响。
- RH→NO2:RH 值的冲击在 1 小时后对 NO2 的影响最大,并且这种影响会随着时间的推移而减弱。IRF 值在 6 小时后达到零。
预测误差方差分解(FEVD)
- FEVD 表示自回归中每个变量对其他变量贡献的信息量。
- 脉冲响应函数追踪一个内生变量的冲击对 VAR 中其他变量的影响,而方差分解则将内生变量的变化分离为 VAR 的各个组成冲击。
- 它确定每个变量的预测误差方差中有多少可以通过对其他变量的外生冲击来解释。
fevd = var_model.fevd(8)
ax = fevd.plot(figsize=(10, 8))
plt.show()
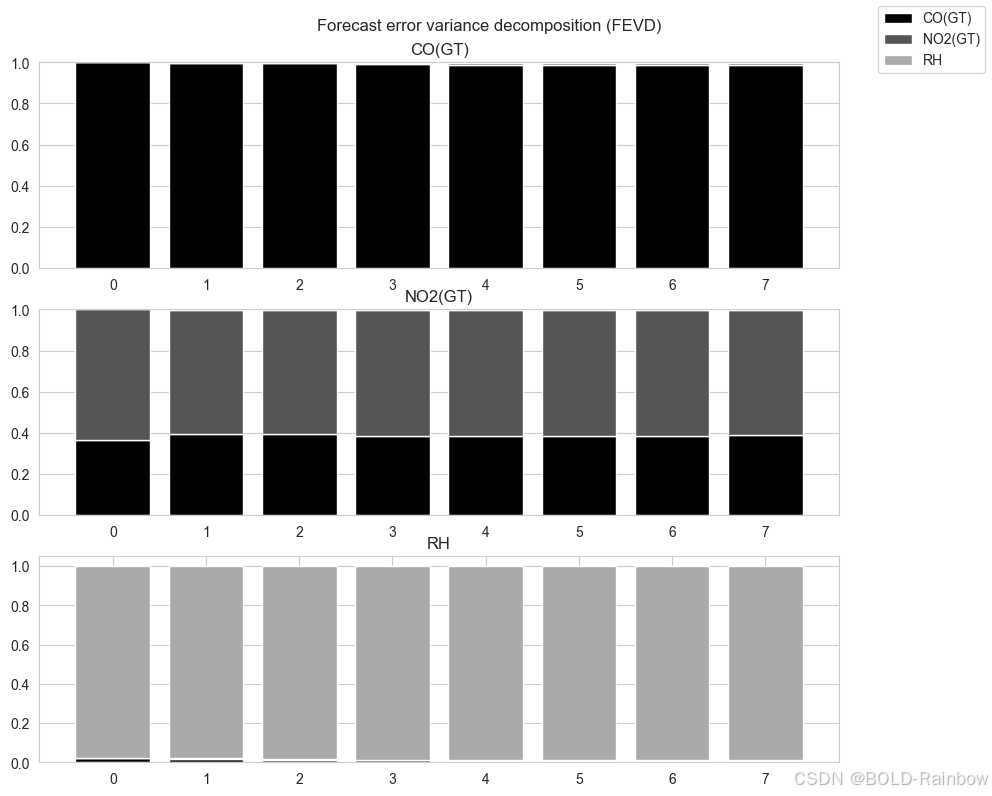
Observations:
- 对于 CO,其差异主要由 CO 的外生冲击来解释。随着时间的推移,CO 的差异会减小,但减小量很小。
- 对于 NO2 而言,其差异主要由 NO2 和 CO 的外部冲击来解释。
- 对于 RH,方差主要由 RH 的外生冲击来解释。随着时间的推移,外生冲击对 CO 的贡献增加。
Example 3. forecasting the Jena climate data
我们尝试使用上述方法预测耶拿气候数据。我们将使用 2019 年 1 月 1 日(00:10)至 2014 年 12 月 29 日(18:10)的每小时天气测量数据训练 VAR 模型。模型的性能将在包含 2014 年 12 月 29 日(19:10)至 2014 年 12 月 31 日(23:20)数据的测试集上进行评估,这相当于每个变量的 17,523 个数据点。
加载数据集
train_df = pd.read_csv('../data/train_series_datetime.csv',index_col=0).set_index('Date Time')
val_df = pd.read_csv('../data/val_series_datetime.csv',index_col=0).set_index('Date Time')
test_df = pd.read_csv('../data/test_series_datetime.csv',index_col=0).set_index('Date Time')
train_df.index = pd.to_datetime(train_df.index)
val_df.index = pd.to_datetime(val_df.index)
test_df.index = pd.to_datetime(test_df.index)
train_val_df = pd.concat([train_df, val_df])
使用ADF检验检查每个变量的平稳性
%%time
test_stat, p_val = [], []
cv_1pct, cv_5pct, cv_10pct = [], [], []
for c in train_val_df.columns:
adf_res = adfuller(train_val_df[c].dropna())
test_stat.append(adf_res[0])
p_val.append(adf_res[1])
cv_1pct.append(adf_res[4]['1%'])
cv_5pct.append(adf_res[4]['5%'])
cv_10pct.append(adf_res[4]['10%'])
adf_res_df = pd.DataFrame({'Test statistic': test_stat,
'p-value': p_val,
'Critical value - 1%': cv_1pct,
'Critical value - 5%': cv_5pct,
'Critical value - 10%': cv_10pct},
index=train_df.columns).T
adf_res_df.round(4)





















 569
569

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








