1.EM算法是含有隐变量的概率模型极大似然估计或极大后验概率估计的迭代算法。含有隐变量的概率模型的数据表示为θ\thetaθ 。这里,YYY是观测变量的数据,ZZZ是隐变量的数据,θ\thetaθ 是模型参数。EM算法通过迭代求解观测数据的对数似然函数L(θ)=logP(Y∣θ){L}(\theta)=\log {P}(\mathrm{Y} | \theta)L(θ)=logP(Y∣θ)的极大化,实现极大似然估计。每次迭代包括两步:
EEE步,求期望,即求logP(Z∣Y,θ)logP\left(Z | Y, \theta\right)logP(Z∣Y,θ) )关于P(Z∣Y,θ(i))P\left(Z | Y, \theta^{(i)}\right)P(Z∣Y,θ(i)))的期望:
Q(θ,θ(i))=∑ZlogP(Y,Z∣θ)P(Z∣Y,θ(i))Q\left(\theta, \theta^{(i)}\right)=\sum_{Z} \log P(Y, Z | \theta) P\left(Z | Y, \theta^{(i)}\right)Q(θ,θ(i))=Z∑logP(Y,Z∣θ)P(Z∣Y,θ(i))
称为QQQ函数,这里θ(i)\theta^{(i)}θ(i)是参数的现估计值;
MMM步,求极大,即极大化QQQ函数得到参数的新估计值:
θ(i+1)=argmaxθQ(θ,θ(i))\theta^{(i+1)}=\arg \max _{\theta} Q\left(\theta, \theta^{(i)}\right)θ(i+1)=argθmaxQ(θ,θ(i))
在构建具体的EM算法时,重要的是定义QQQ函数。每次迭代中,EM算法通过极大化QQQ函数来增大对数似然函数L(θ){L}(\theta)L(θ)。
2.EM算法在每次迭代后均提高观测数据的似然函数值,即
P(Y∣θ(i+1))⩾P(Y∣θ(i))P\left(Y | \theta^{(i+1)}\right) \geqslant P\left(Y | \theta^{(i)}\right)P(Y∣θ(i+1))⩾P(Y∣θ(i))
在一般条件下EM算法是收敛的,但不能保证收敛到全局最优。
3.EM算法应用极其广泛,主要应用于含有隐变量的概率模型的学习。高斯混合模型的参数估计是EM算法的一个重要应用,下一章将要介绍的隐马尔可夫模型的非监督学习也是EM算法的一个重要应用。
4.EM算法还可以解释为FFF函数的极大-极大算法。EM算法有许多变形,如GEM算法。GEM算法的特点是每次迭代增加FFF函数值(并不一定是极大化FFF函数),从而增加似然函数值。
在统计学中,似然函数(likelihood function,通常简写为likelihood,似然)是一个非常重要的内容,在非正式场合似然和概率(Probability)几乎是一对同义词,但是在统计学中似然和概率却是两个不同的概念。概率是在特定环境下某件事情发生的可能性,也就是结果没有产生之前依据环境所对应的参数来预测某件事情发生的可能性,比如抛硬币,抛之前我们不知道最后是哪一面朝上,但是根据硬币的性质我们可以推测任何一面朝上的可能性均为50%,这个概率只有在抛硬币之前才是有意义的,抛完硬币后的结果便是确定的;而似然刚好相反,是在确定的结果下去推测产生这个结果的可能环境(参数),还是抛硬币的例子,假设我们随机抛掷一枚硬币1,000次,结果500次人头朝上,500次数字朝上(实际情况一般不会这么理想,这里只是举个例子),我们很容易判断这是一枚标准的硬币,两面朝上的概率均为50%,这个过程就是我们运用出现的结果来判断这个事情本身的性质(参数),也就是似然。
P(Y∣θ)=∏[πpyi(1−p)1−yi+(1−π)qyi(1−q)1−yi]P(Y|\theta) = \prod[\pi p^{y_i}(1-p)^{1-y_i}+(1-\pi) q^{y_i}(1-q)^{1-y_i}]P(Y∣θ)=∏[πpyi(1−p)1−yi+(1−π)qyi(1−q)1−yi]
E step:
μi+1=π(pi)yi(1−(pi))1−yiπ(pi)yi(1−(pi))1−yi+(1−π)(qi)yi(1−(qi))1−yi\mu^{i+1}=\frac{\pi (p^i)^{y_i}(1-(p^i))^{1-y_i}}{\pi (p^i)^{y_i}(1-(p^i))^{1-y_i}+(1-\pi) (q^i)^{y_i}(1-(q^i))^{1-y_i}}μi+1=π(pi)yi(1−(pi))1−yi+(1−π)(qi)yi(1−(qi))1−yiπ(pi)yi(1−(pi))1−yi
M step:
πi+1=1n∑j=1nμji+1\pi^{i+1}=\frac{1}{n}\sum_{j=1}^n\mu^{i+1}_jπi+1=n1j=1∑nμji+1pi+1=∑j=1nμji+1yi∑j=1nμji+1p^{i+1}=\frac{\sum_{j=1}^n\mu^{i+1}_jy_i}{\sum_{j=1}^n\mu^{i+1}_j}pi+1=∑j=1nμji+1∑j=1nμji+1yiqi+1=∑j=1n(1−μji+1yi)∑j=1n(1−μji+1)q^{i+1}=\frac{\sum_{j=1}^n(1-\mu^{i+1}_jy_i)}{\sum_{j=1}^n(1-\mu^{i+1}_j)}qi+1=∑j=1n(1−μji+1)∑j=1n(1−μji+1yi)
class EM:
def __init__(self, prob):
self.pro_A, self.pro_B, self.pro_C = prob
# e_step
def pmf(self, i):
pro_1 = self.pro_A * math.pow(self.pro_B, data[i]) * math.pow(
(1 - self.pro_B), 1 - data[i])
pro_2 = (1 - self.pro_A) * math.pow(self.pro_C, data[i]) * math.pow(
(1 - self.pro_C), 1 - data[i])
return pro_1 / (pro_1 + pro_2)
# m_step
def fit(self, data):
count = len(data)
print('init prob:{}, {}, {}'.format(self.pro_A, self.pro_B,
self.pro_C))
for d in range(count):
_ = yield
_pmf = [self.pmf(k) for k in range(count)]
pro_A = 1 / count * sum(_pmf)
pro_B = sum([_pmf[k] * data[k] for k in range(count)]) / sum(
[_pmf[k] for k in range(count)])
pro_C = sum([(1 - _pmf[k]) * data[k]
for k in range(count)]) / sum([(1 - _pmf[k])
for k in range(count)])
print('{}/{} pro_a:{:.3f}, pro_b:{:.3f}, pro_c:{:.3f}'.format(
d + 1, count, pro_A, pro_B, pro_C))
self.pro_A = pro_A
self.pro_B = pro_B
self.pro_C = pro_C
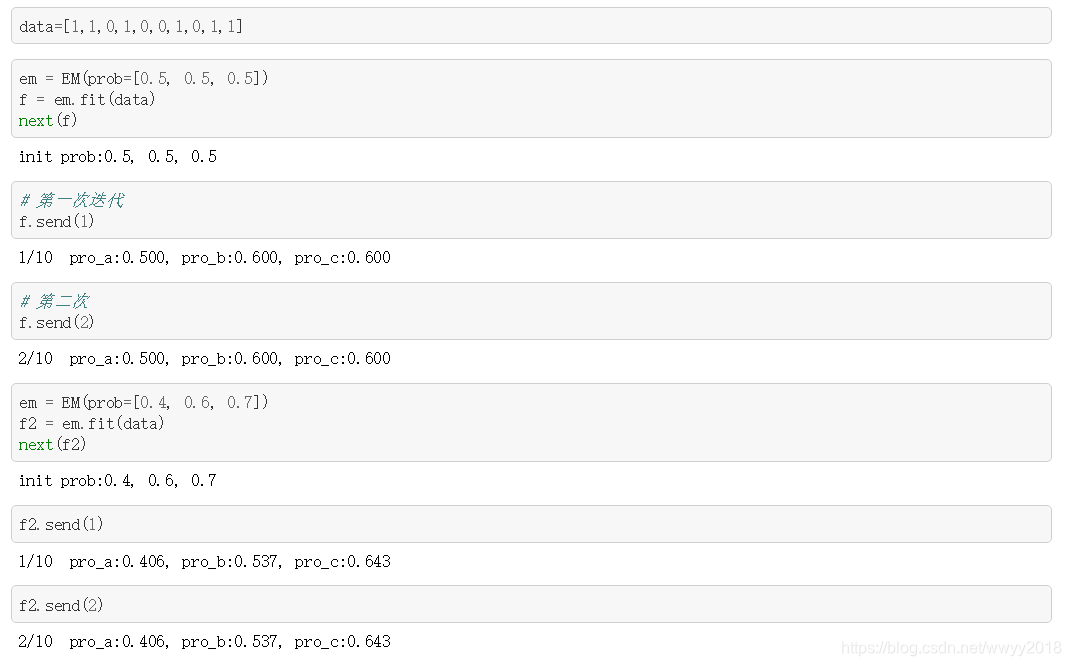





 EM算法是一种用于含有隐变量的概率模型极大似然估计的迭代算法,通过求期望和极大化步骤迭代更新参数估计,每次迭代均能提高观测数据的似然函数值。EM算法在高斯混合模型和隐马尔可夫模型等概率模型学习中有广泛应用。
EM算法是一种用于含有隐变量的概率模型极大似然估计的迭代算法,通过求期望和极大化步骤迭代更新参数估计,每次迭代均能提高观测数据的似然函数值。EM算法在高斯混合模型和隐马尔可夫模型等概率模型学习中有广泛应用。

















 1225
1225

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










