动态规划(一)

动态规划是一种解决多阶段决策过程最优化问题的算法。它将大问题分解为小问题，通过维护中间状态的方式，避免了暴力求解的重复计算，来提高求解的效率。

动态规划与暴力递归的区别在于，动态规划会将中间状态记录下来，避免重复计算，而暴力递归则没有这个优化。

动态规划通常分为以下几个步骤：

1. 定义状态：定义问题的状态，通常使用一维或二维数组来表示。
2. 初始化状态：将问题的初始状态赋值到数组中。
3. 状态转移方程：定义状态之间的转移方式，通常使用递推公式表示。
4. 计算结果：根据状态转移方程计算问题的最终结果。

动态规划算法具有以下性质：

1. 最优子结构：问题的最优解可以由子问题的最优解推导得出。
2. 无后效性：某阶段状态一旦确定，就不受这个状态以后决策的影响。
3. 重复子问题：问题可以被分解成许多子问题，这些子问题具有重叠的部分。

动态规划算法可以用来解决很多实际问题，下面以一个游戏：使用动态规划实现小白兔拔萝卜问题

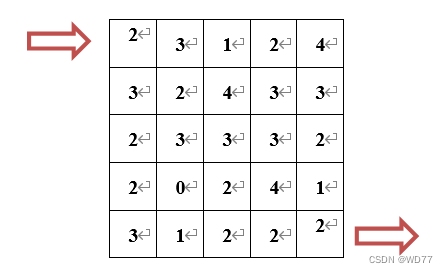
表格中显示的是一片萝卜田，小白兔从田地的左上角进入，在右下角离开，每次必须选择向下或者向右走一格，并拿走格子里的萝卜。求小白兔获得的最大萝卜数量和走过的路径。

#include<stdlib.h>
#include<stdio.h>
#include<time.h>
const int M=5; //萝卜地行数 
const int N=5; //萝卜地列数 
int v[M][N];  //萝卜地中的萝卜数 
int c[M][N];  //每块地从（0，0）出发的最优萝卜数 
int dituiluobo(int m,int n)
{
	int i,j;
	c[0][0]=v[0][0];
	for(i=1;i<=m;i++)
		c[i][0]=c[i-1][0]+v[i][0]; 
	for(j=1;j<=n;j++)
		c[0][j]=c[0][j-1]+v[0][j];
	for(i=1;i<=m;i++)
		for(j=1;j<=n;j++)
		{
			if(c[i-1][j]>=c[1][j-1])
				c[i][j]=c[i-1][j]+v[i][j];
			else
				c[i][j]=c[i][j-1]+v[i][j]; 
		}
		return c[m][n];
}


void TrackSolution(int m,int n)
{
	printf("%d,%d\n",m,n);
	while(m!=0||n!=0)
	{
		if(m==0)
		{
			n--;
			printf("%d,%d\n",m,n);
		}
		else if(n==0)
		{
			m--;
			printf("%d,%d\n",m,n);
		}
		else if(c[m-1][n]>=c[m][n-1])
		{
			m--;
			printf("%d,%d\n",m,n);
		}
		else
		{
			n--;
			printf("%d,%d\n",m,n);
		 } 
	}
}
int main()
{
	int i,j,start,end,t,count;
	printf("随机生成萝卜地如下：\n");
	for(i=0;i<M;i++)
	{
		for(j=0;j<N;j++)
		{
			v[i][j]=rand()%10;
			c[i][j]=0;
			printf("%d\t",v[i][j]);
		}
		printf("\n");
	}
	count=dituiluobo(M-1,N-1);
	printf("萝卜矩阵如下：\n");
	for(i=0;i<M;i++)
	{
		for(j=0;j<N;j++)
		{
			printf("%d\t",c[i][j]);
		}
		printf("\n");
	}
	printf("TrackSolution（追踪解）如下：\n");
	TrackSolution(M-1,N-1);
	return 1;
}

动态规划算法非常强大，可用来解决很多实际问题。在应用动态规划算法时，需要注意定义状态、初始化状态、状态转移方程和计算结果等步骤，同时可以通过优化策略来提高算法的效率。