leetcode5:最长回文子串

这个题目想到n的3次方的复杂度站起来，我先站起来了各位！这道题难度只是复杂，只是复杂，我好菜啊。

这里写两种一种n的平方时间复杂度：确切的来说不止n的平方吧

//解法1
public static String longestPalindrome(String s) {
        String returnS = "";
        for(int i=0;i<s.length();i++){
            for(int j=i+1;j<=s.length();j++){
                String che = s.substring(i, j);
                if(checkIt(che) && che.length()>returnS.length()){
                    returnS = che;
                }
            }
        }
        return returnS;

    }

    public static Boolean checkIt(String s) {
        if(s.length()==0) return true;
        else if(s.length()==1) return true;
        else{
            return checkIt(s.substring(1,s.length()-1))&&s.charAt(0)==s.charAt(s.length()-1);
        }
    }

测试方法:

public static void main(String[] args) {
        String s = "civilwartestingwhetherthatnaptionoranynartionsoconceivedandsodedicatedcanlongendureWeareqmetonagreatbattlefiemldoftzhatwarWehavecometodedicpateaportionofthatfieldasafinalrestingplaceforthosewhoheregavetheirlivesthatthatnationmightliveItisaltogetherfangandproperthatweshoulddothisButinalargersensewecannotdedicatewecannotconsecratewecannothallowthisgroundThebravelmenlivinganddeadwhostruggledherehaveconsecrateditfaraboveourpoorponwertoaddordetractTgheworldadswfilllittlenotlenorlongrememberwhatwesayherebutitcanneverforgetwhattheydidhereItisforusthelivingrathertobededicatedheretotheulnfinishedworkwhichtheywhofoughtherehavethusfarsonoblyadvancedItisratherforustobeherededicatedtothegreattdafskremainingbeforeusthatfromthesehonoreddeadwetakeincreaseddevotiontothatcauseforwhichtheygavethelastpfullmeasureofdevotionthatweherehighlyresolvethatthesedeadshallnothavediedinvainthatthisnationunsderGodshallhaveanewbirthoffreedomandthatgovernmentofthepeoplebythepeopleforthepeopleshallnotperishfromtheearth";
        Long start = System.nanoTime();
        String returns = longestPalindrome(s);
        Long end = System.nanoTime();

        System.out.println("结果:" + returns + "用时(纳秒):" + (end - start));
    }

 这个s很长，这是leetcode上面测试用例通不过的，时间超出界限

运行下来时间:

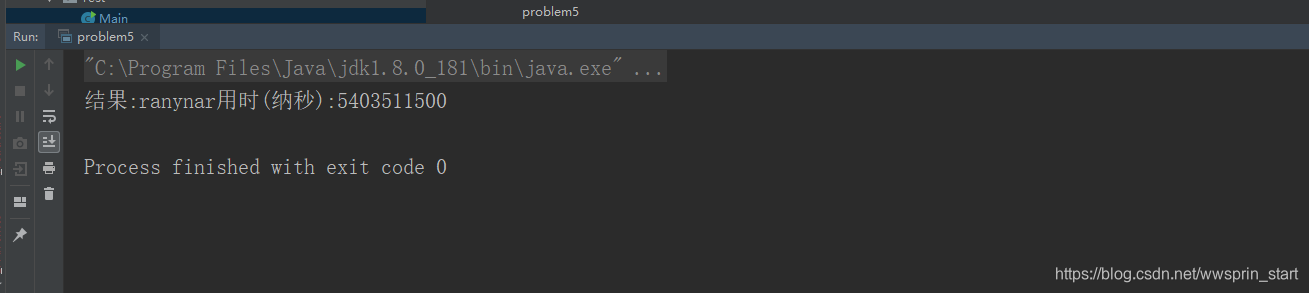
就是5秒钟，

然后官方给的最牛逼的方法:

方法二:

采用的是中心点的方法，就是假设i，或者i和i+1是这个回文字串S的中心点，因为这个回文串S的长度可能是偶数也可能是奇数，是中心点了，那么他左右两边去发展，然后如果他的L+1和他的R+1（L表示字符串S左边坐标，R表示字符串S右边坐标）相等那么它就是个回文串，然后记录下它的长度，方法findCenter就是找到left和right为中心部分的像两边扩展的最大回文字串的长度，然后返回给主方法，主方法判断这个你够不够长，如果比原来的长，那么就修改下start和end，改成现在的样子，

细节部分就是截取字符串的时候start = i - (lenght-1)/2; end = i + lenght / 2;这样就保证了，不管你是以i或者i和i+1为中心点的字符串，都能够截取到想要的东东，掏出自己的小本本，默默的记下来。

话说，这方法是leetcode上面的官方解答，我为什么要在这边抄一遍，搬砖搬习惯了，顺手了，对不起，打扰了。

记录下来而已，谢谢！

public static String longestPalindrome(String s) {
        if(s==null || s.length()<=1) return s;
        int start = 0;
        int end = 0;
        for(int i=0;i<s.length();i++){
            int len1 = findCenter(s, i, i + 1);
            int len2 = findCenter(s, i, i);
            int lenght = Math.max(len1, len2);
            if (lenght > end-start+1) {
                start = i - (lenght-1)/2;
                end = i + lenght / 2;
            }
        }
        return s.substring(start,end+1);

    }

    public static int findCenter(String s,int left,int right){
        int L = left, R = right;
        while (L>=0&&R<s.length()&&s.charAt(L)==s.charAt(R)){
            L--;
            R++;
        }
        //这里的R位置和L位置已经不能符合要求，因此R-L-1，而不是R-L+1
        return R-L-1;

    }

运行后结果:

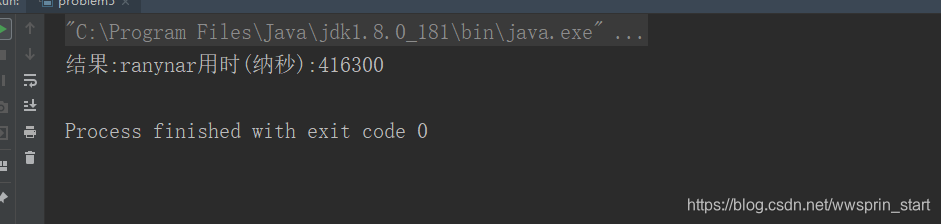
看看这方法的速度，一个是约等于5秒，一个是0.5毫秒，相差万倍。这时候想喊一声差距咋就这么大呢